二阶系统时域分析：从特征根到单位阶跃响应

"自动控制原理：第8讲（第三章 二阶系统时域分析）.pptx" 自动控制原理中的二阶系统时域分析是控制理论中的核心概念，主要研究二阶动态系统的响应特性。本讲主要围绕二阶系统的微分方程、传递函数以及系统参数对性能的影响进行深入探讨。 首先，二阶系统是指其动态行为由二阶微分方程描述的控制系统。这个微分方程通常以如下形式表示： \[ \ddot{x}(t) + 2\zeta\omega_n\dot{x}(t) + \omega_n^2x(t) = u(t) \] 其中，\( \ddot{x}(t) \) 是加速度，\( \dot{x}(t) \) 是速度，\( x(t) \) 是位置，\( u(t) \) 是输入，\( \zeta \) 是阻尼比，\( \omega_n \) 是自然振荡频率。通过传递函数，我们可以将二阶系统转换为更通用的形式，以便于分析。 在Simulink环境中，可以通过改变系统参数K和T来观察系统响应的变化。K是增益，T是时间常数，它们共同决定了系统的动态特性。将系统表示为标准形式，即闭环传递函数为： \[ G_c(s) = \frac{K}{s^2 + 2\zeta\omega_n s + \omega_n^2} \] 二阶系统的两个关键参数是自然振荡频率\( \omega_n \)和阻尼比\( \zeta \)。自然振荡频率描述了系统在没有阻尼情况下的自由振荡频率，而阻尼比则决定了系统衰减振荡的速度。系统的响应特性，如上升时间、超调量和调节时间，完全由这两个参数决定。 根据闭环特征方程： \[ s^2 + 2\zeta\omega_n s + \omega_n^2 = 0 \] 二阶系统的特征根可以是两个共轭复数、两个相等的实数或一对正实数。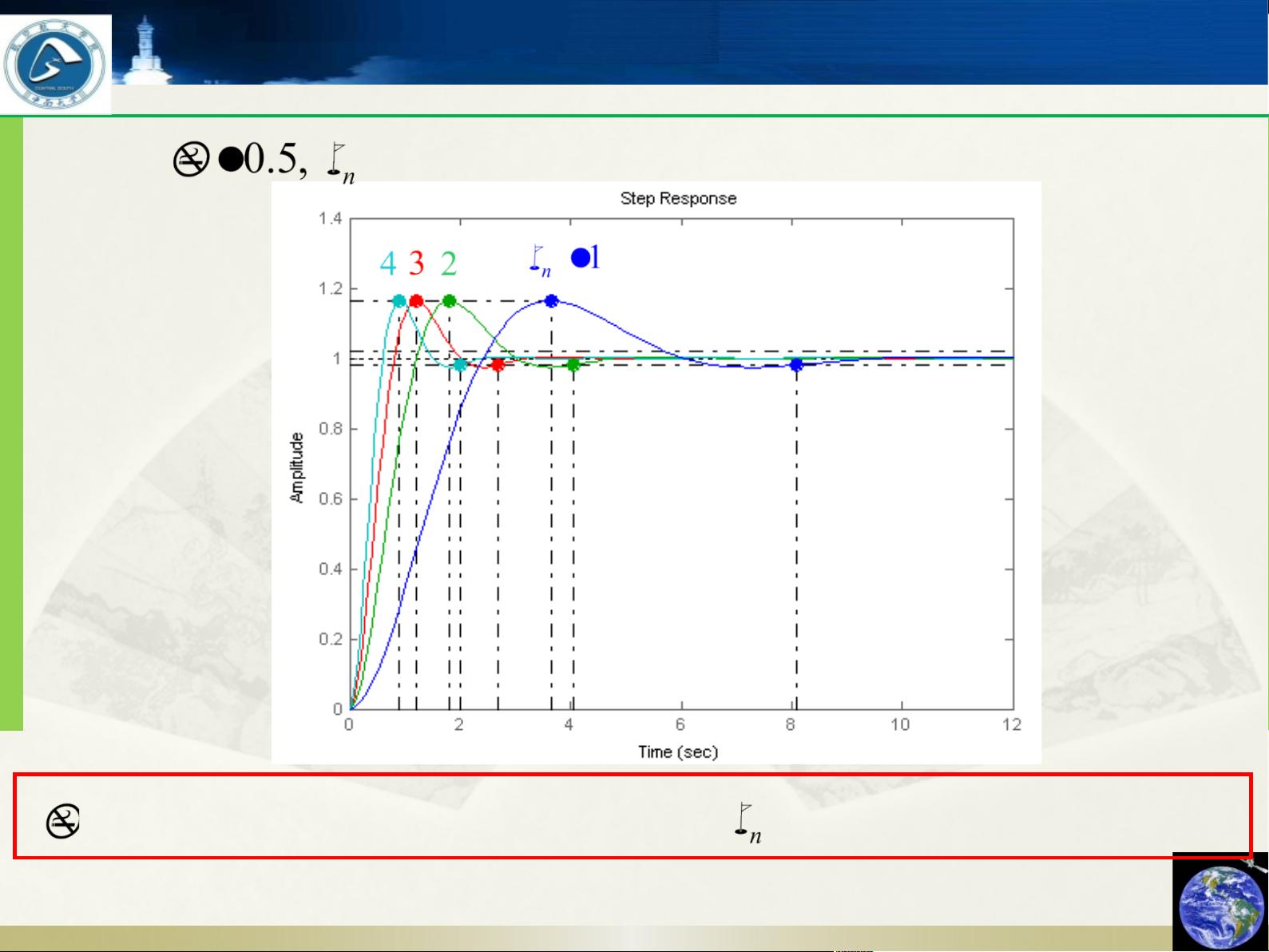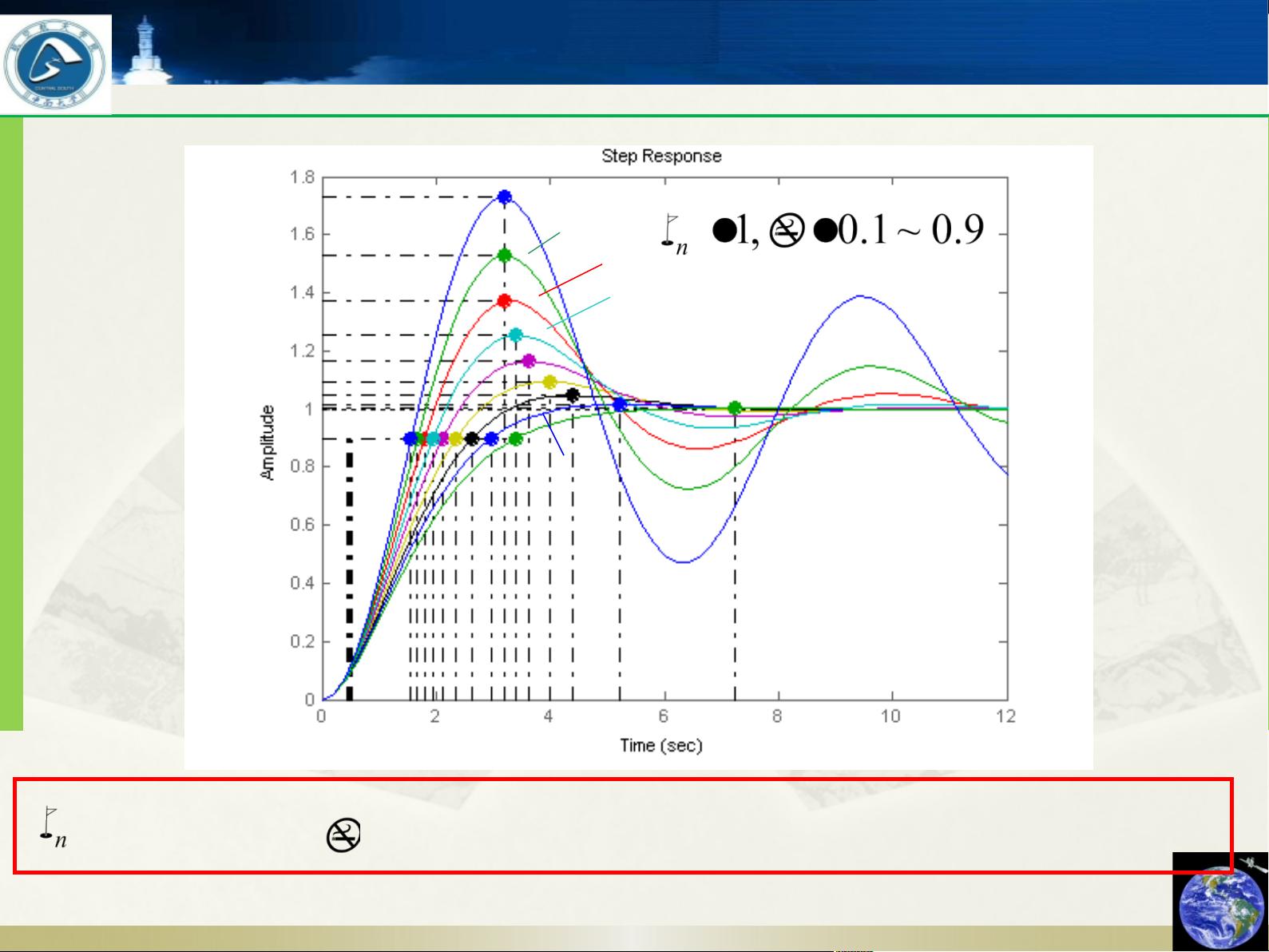不同类型的特征根对应着不同的系统响应特性： 1. 欠阻尼系统（\( 0 < \zeta < 1 \)）：特征根为一对共轭复数，表现为衰减的正弦振荡。超调量和衰减速率都与阻尼比有关，阻尼比越大，衰减越快，超调量越小。 2. 临界阻尼系统（\( \zeta = 1 \)）：特征根为两个相等的实数，响应无振荡，单调上升，达到稳态值的速度最快。 3. 过阻尼系统（\( \zeta > 1 \)）：特征根为两个不相等的实数，响应呈现非振荡的指数衰减，达到稳态值的速度较慢。 通过Simulink仿真和理论分析，我们可以清晰地看到这些不同阻尼状态下的系统响应。例如，当增加阻尼比时，系统的响应速度会变慢，超调量减小；反之，减小阻尼比会使得系统响应更快，但可能会导致更大的超调。 二阶系统时域分析是理解和设计控制系统的关键步骤，它帮助我们理解和优化系统的动态行为，以满足特定的性能指标，如快速性、稳定性、抗干扰能力等。通过调整系统参数，可以实现对系统性能的有效控制，从而在实际工程应用中实现精确的控制效果。