图像处理中的傅里叶变换：分解频率成分与应用

傅里叶变换是一种在信号处理和数学分析中至关重要的工具，它能够将一个时域信号分解成不同频率的组件，提供信号在频域中的表示。在图像处理领域，傅里叶变换起着关键作用，因为它能揭示信号的频率组成和各频率分量的大小，这对于分析复杂信号如噪声干扰的多频率成分信号尤其有价值。 一维傅里叶变换（FT）是连续函数f(x)到频率域函数F(u)的转换，其定义为： 连续傅里叶变换: \( F(u) = \int_{-\infty}^{\infty} f(x) e^{-j2\pi xu} dx \) 其反变换则为: \( f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(u) e^{j2\pi xu} du \) 对于离散信号，一维离散傅里叶变换（DFT）基于离散点计算，其定义为： \( F(u) = \sum_{n=0}^{N-1} f(n) e^{-j2\pi un/N} \) 离散傅里叶变换的反变换同样存在，可以利用欧拉公式简化计算。通过DFT，我们可以通过不同的u值（频率成分）来观察信号的不同频率特性。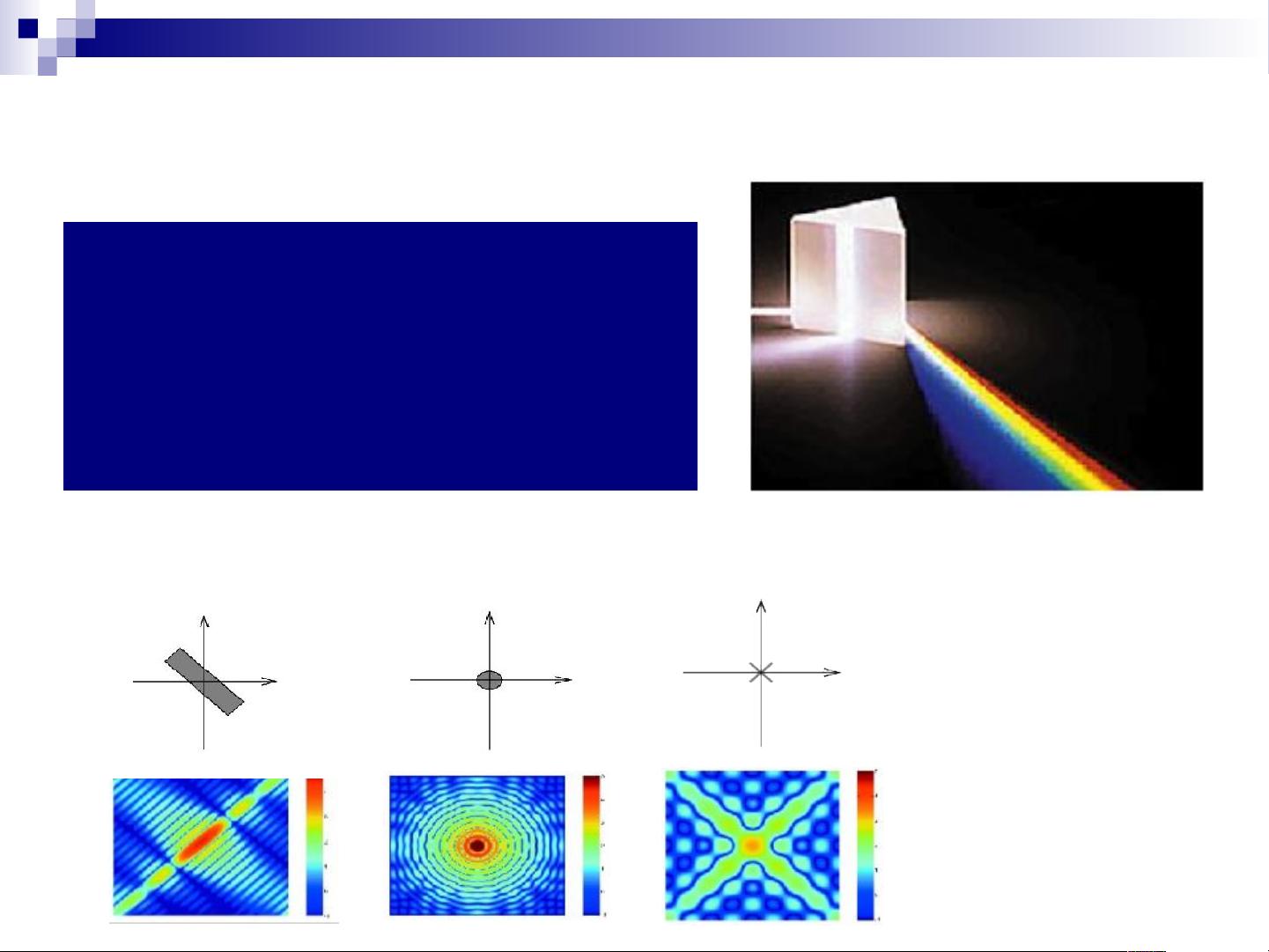 傅里叶变换的主要作用包括： 1. **频率分解**：将信号分解成一系列的频率成分，类似于光学中的分色棱镜将白光分解为不同颜色。 2. **信号成分**：识别出直流分量（信号的平均值）和交流分量（周期性变化），有助于理解信号的波动特性。 3. **频率与变化速度**：信号中噪声、边缘、跳跃等细节通常对应高频成分，而平滑背景和慢变化区域则对应低频成分。 二维傅里叶变换（2D DFT）扩展了一维概念，适用于处理二维图像。对于图像尺寸为M×N的函数f(x,y)，其2D DFT为： \( F(u,v) = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m,n) e^{-j2\pi (um/M + vn/N)} \) 通过这种变换，我们可以获得图像在各个频率方向上的信息，进一步进行滤波、压缩、编码等图像处理操作。 傅里叶变换是一种强大的工具，它在信号处理、通信工程、图像处理等多个领域都有着广泛的应用，对于理解和分析复杂信号的频域特性至关重要。理解并熟练掌握傅里叶变换原理和技术是任何从事相关工作专业人员的必备技能。