点到直线距离算法详解:效率优化与比较
"本文介绍了计算点到直线距离的三种方法,重点讲述了矢量算法,强调其在效率上的优势。同时,也探讨了点到线段最短距离的计算,区分了点在线段上和在线段延长线上的不同情况。文章提到了经典算法和面积算法,分析了各自的优缺点。经典算法虽然直观但计算量大,不适合大量运算;面积算法思路清晰,但计算过程中涉及多次平方和开方运算,也可能导致计算负担。"
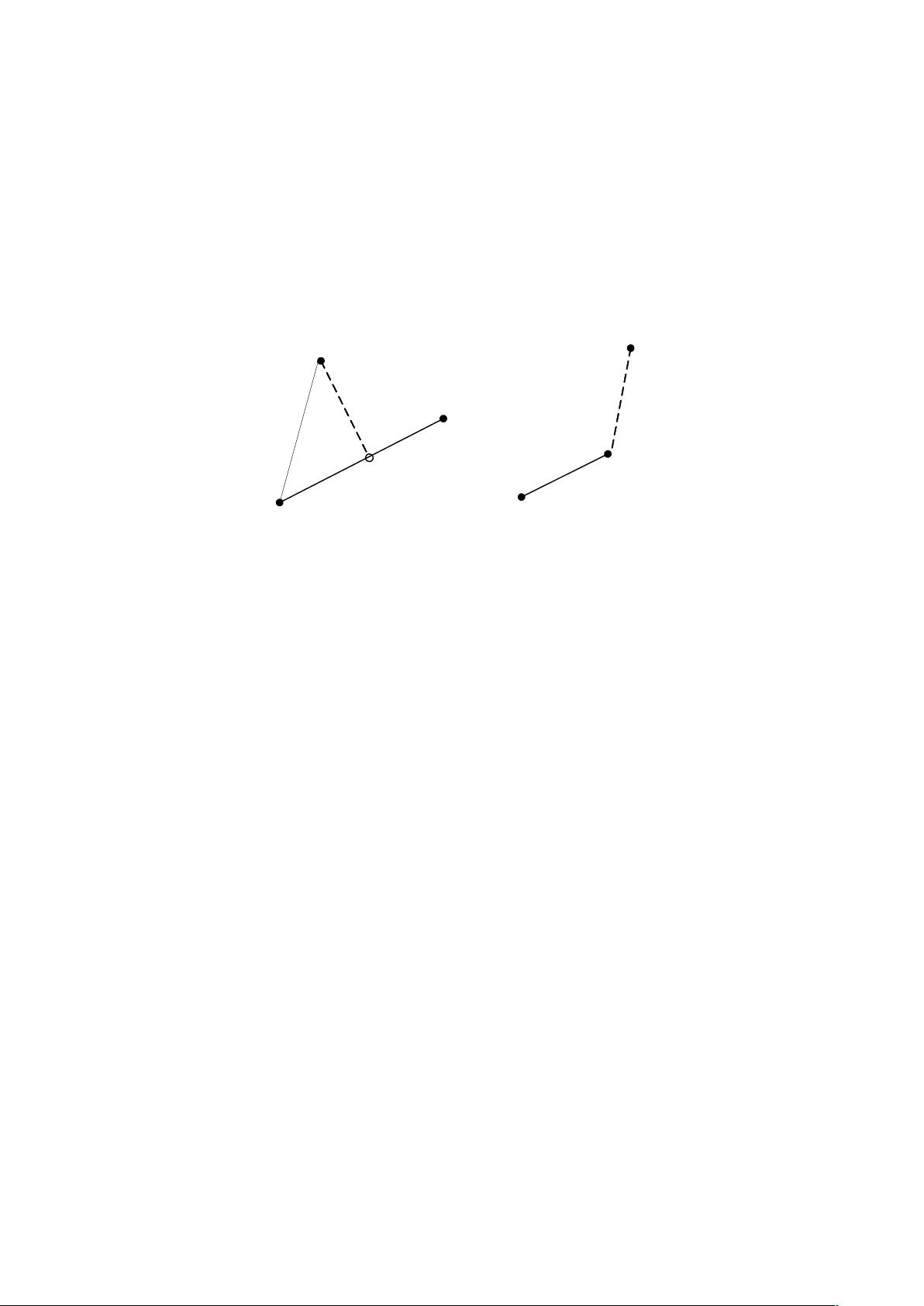
在计算机图形学和几何算法中,求解点到直线的距离是一个常见的问题。本文主要讨论了三种解决方法,针对点到线段的最短距离进行了详细阐述,因为这与点到直线的距离有所不同,需要考虑点在线段上的投影是否落在线段上。
首先,经典算法基于高中解析几何知识,通过比较点的位置关系(如在线段端点、在线上等)并进行一系列的几何判断来求解。这种方法易于理解,但其缺点在于计算复杂,尤其在处理大量线段的情况时,效率低下,而且算法中的特定函数可能不便于在不同编程语言间移植。
其次,面积算法利用了同底等高的三角形面积相等的性质来求解。当点的投影在线段上时,可以通过计算参考点与线段端点构成的三角形的高来得到最短距离。这种方法的代码实现较为直观,但计算过程中需要多次进行平方和开方运算,这在大量运算时会增加计算负担。
最后,矢量算法通常被认为是最有效的方法。它利用向量的点积和模长来计算点到直线的距离,公式简洁,计算量相对较小。对于点到线段的距离,可以通过判断投影点位置来调整。矢量算法的优势在于其数学基础坚实,适用于各种编程环境,且计算效率高,尤其适合处理大量数据。
选择哪种算法取决于具体的应用场景和性能需求。对于简单的情况,经典算法可能足够;对于需要高效计算和跨语言移植的场景,矢量算法通常是更好的选择。而面积算法则提供了一种中间道路,尽管计算复杂度较高,但在某些特定情况下可能更直观易懂。理解这些算法并根据实际需求选择合适的方法,是解决此类问题的关键。
2022-08-04 上传
208 浏览量
168 浏览量
288 浏览量
2024-12-13 上传
245 浏览量
junjie0314
- 粉丝: 1
- 资源: 4
最新资源
- SQL SERVER实用经验技巧集
- 程序设计需求分析模板
- 15天学会jQuery(0-5).15天学会jQuery(0-5).
- Android编程指南(en)
- White-Box Testing
- mtk经典方案pdf
- Java 程序语言设计
- signaling 7
- AT91RM9200 中断控制器详解(AIC)
- ADO.Net完全攻略.pdf
- Building embeded Linux
- Class Discussion 2 - HP
- 《计算机软件文档编制规范》GB-T8567-2006 (文档结构已整理,word版)
- 数字功率放大器数字PWM线性化技术
- 2008惠普的一次考试题
- UNIX系统操作命令