一维波动方程数值解：边界条件对反射与损失的影响

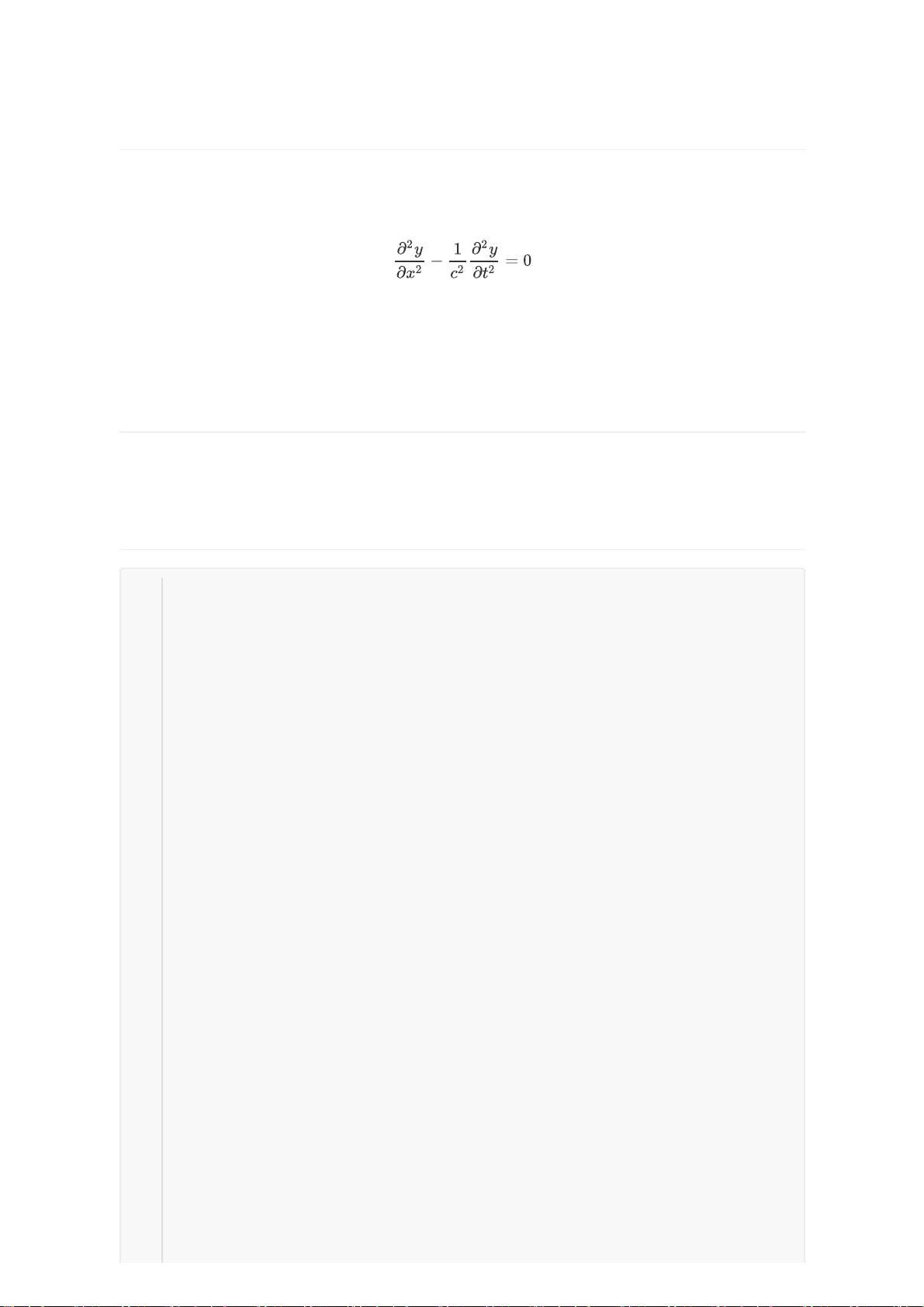
一维波动方程的数值解1深入探讨了如何通过数值方法模拟一维波动现象，特别是在MATLAB编程环境下实现其解决过程。该文章的核心内容围绕着一维波动方程的数学表达式： \[ \frac{\partial^2 y}{\partial t^2} = c^2 \frac{\partial^2 y}{\partial x^2} \] 其中 \( y(x,t) \) 是时间和空间的函数，\( c \) 是波速。文章介绍了一种常用的数值求解方法——有限差分法，它将连续问题离散化为网格上的离散方程。在本例中，空间被划分为 \( N_x \) 个等间距的点，时间被划分为 \( N_t \) 个等时间间隔。 有限差分法用于近似二阶导数，例如对于边界条件，文中提到了两种常见类型：Dirichlet边界条件（令 \( y(x,t) = 0 \) 在边界），在这种情况下，波会经历全反射并伴随半波损失；另一种是Neumann边界条件（\( \frac{\partial y}{\partial x} = 0 \)），波同样反射，但无半波损失。为了模拟这种反射，程序使用了一个二阶差分公式 \( D_2 \) 来更新函数值，并在每个时间步长 \( dt \) 内根据边界条件进行调整。 MATLAB代码中，`wave1D` 函数定义了一系列变量，如波速 \( c \)，空间和时间范围，以及网格数量。初始条件 `y0(x,k,Ncyc)` 定义了初始波包的形状和周期数。程序通过循环迭代，每次时间步长更新函数值，并在每个时间步用 `bc_set` 函数处理边界条件，确保正确反映物理现象。 在`for`循环中，每8次迭代会清空当前图形窗口，重新绘制 \( y(x,t) \) 的分布，并用散点标记边界点以可视化波的反射。通过这个过程，读者可以观察到波在不同边界条件下的传播和反射行为。 总结来说，本文提供了一个使用MATLAB实现的一维波动方程数值解的详细步骤，涵盖了方程的离散化处理、边界条件的设置以及如何利用有限差分法模拟波动现象中的反射过程，这对于理解和应用数值计算方法来处理物理问题具有实际价值。