Python图算法对比：Bellman-Ford与Dijkstra最短路径解析

"这篇文档是关于Python中对比分析Bellman-Ford和Dijkstra两种最短路径算法的技术资料。文档详细介绍了这两种算法的背景、特点以及它们在处理加权图最短路径问题上的应用。" 在计算机科学中，寻找图中的最短路径是一个常见的问题，特别是在网络路由、地图导航等领域。本篇文档主要探讨了针对加权图的Bellman-Ford算法和Dijkstra算法，这两种算法都是解决此类问题的有效方法。 1. 贝尔曼-福特（Bellman-Ford）算法 Bellman-Ford算法由理查德·贝尔曼和莱斯特·福特提出，适用于处理存在负权重边的图。尽管其时间复杂度较高，为O(m * n)，其中m为边的数量，n为顶点的数量，但由于它可以处理负权重边，因此在某些场景下仍然是必要的。算法的核心思想是通过松弛操作不断更新各个顶点的最短路径估计值，直到所有可能的路径都被考虑过，或者在n-1次迭代后没有进一步的更新，表明不存在负权环。 2. Dijkstra算法 Dijkstra算法由艾兹格·迪科斯彻发明，主要处理的是没有负权重边的图，它采用贪心策略，每次选取当前已知最短路径到达的未访问顶点，并更新其邻居节点的最短路径估计值。Dijkstra算法的时间复杂度在使用优先队列（如二叉堆）实现时可以达到O((m+n) log n)，效率相对较高。然而，由于它不支持负权重边，一旦遇到负权重，算法将无法正确工作。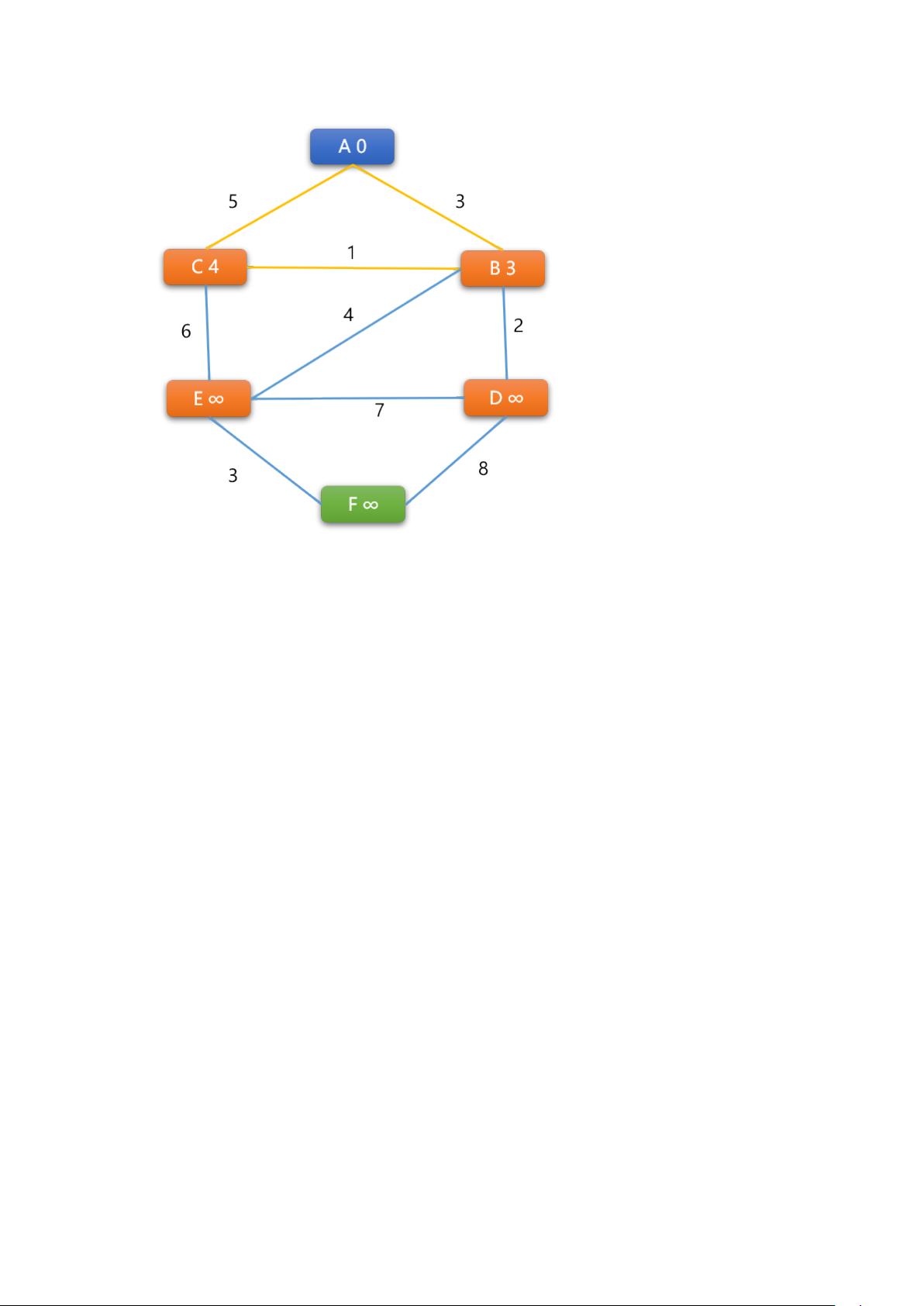 文档中提到了这两种算法的工作原理，并通过一个具体的无向加权图示例展示了它们的运行过程。例如，在这个例子中，从顶点A出发，Bellman-Ford算法会逐步更新所有顶点的最短路径，而Dijkstra算法则会从A开始，依次找到到其他顶点的最短路径，如B、C等。 3. 其他算法 除了Bellman-Ford和Dijkstra，文档还提及了A*算法和D*算法，这两种算法是在搜索领域常用的启发式搜索策略，它们结合了Dijkstra算法的特性并引入了启发函数来引导搜索，通常用于寻找最优路径，尤其是在实时导航系统和游戏AI中。 这篇文档深入浅出地解释了两种重要的最短路径算法，对于理解图论中的路径搜索问题具有很大的帮助。无论是开发网络路由软件，还是设计游戏中的智能路径规划，这些算法都是不可或缺的基础知识。