红黑树算法详解：插入、删除与旋转

"红黑树算法(算法导论) 详解 【for_wind】" 红黑树是一种自平衡的二叉查找树（BST），由鲁道夫·贝尔在1972年提出，其名称来源于节点可能的颜色：红色或黑色。红黑树的主要目标是保持树的平衡，从而在插入、删除和查找操作中保持高效的性能，通常为O(logn)的时间复杂度。 **二叉查找树** 是红黑树的基础，它的每个节点包含一个关键字key，以及指向左子节点、右子节点和父节点的指针。在二叉查找树中，节点的左子树包含的所有元素都小于或等于该节点，而右子树包含的所有元素都大于或等于该节点。这种特性使得查找、插入和删除操作相对高效。 **红黑树的性质** 包括： 1. 每个节点要么是红色，要么是黑色。 2. 根节点是黑色。 3. 所有叶子节点（NIL或空节点）是黑色。 4. 如果一个节点是红色，则它的两个子节点都是黑色。 5. 对每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点（即黑色高度）。 **操作描述**： - **插入**：当插入新节点时，初始设置为红色，然后通过调整节点颜色和旋转（左旋或右旋）来维护红黑树的性质。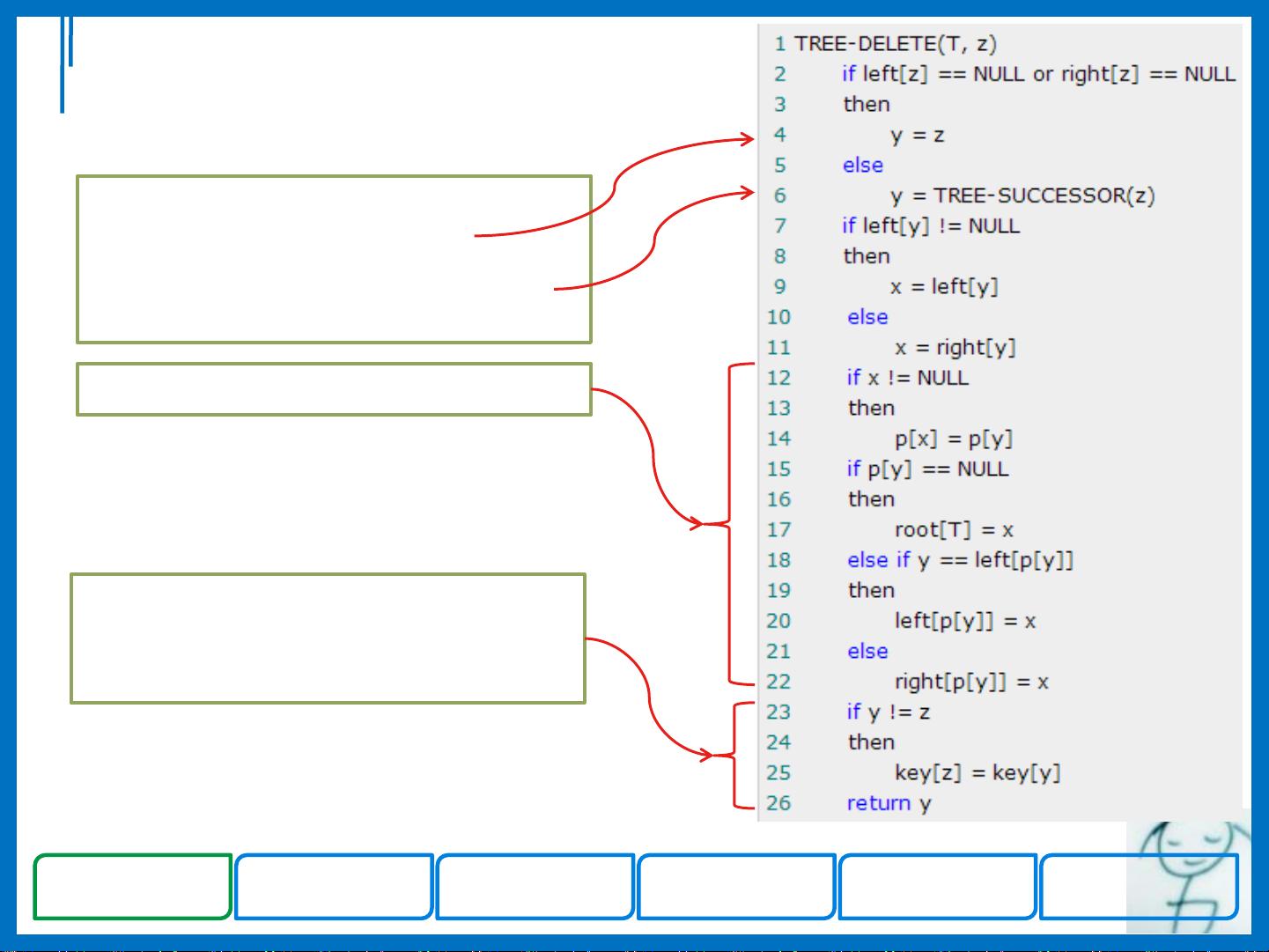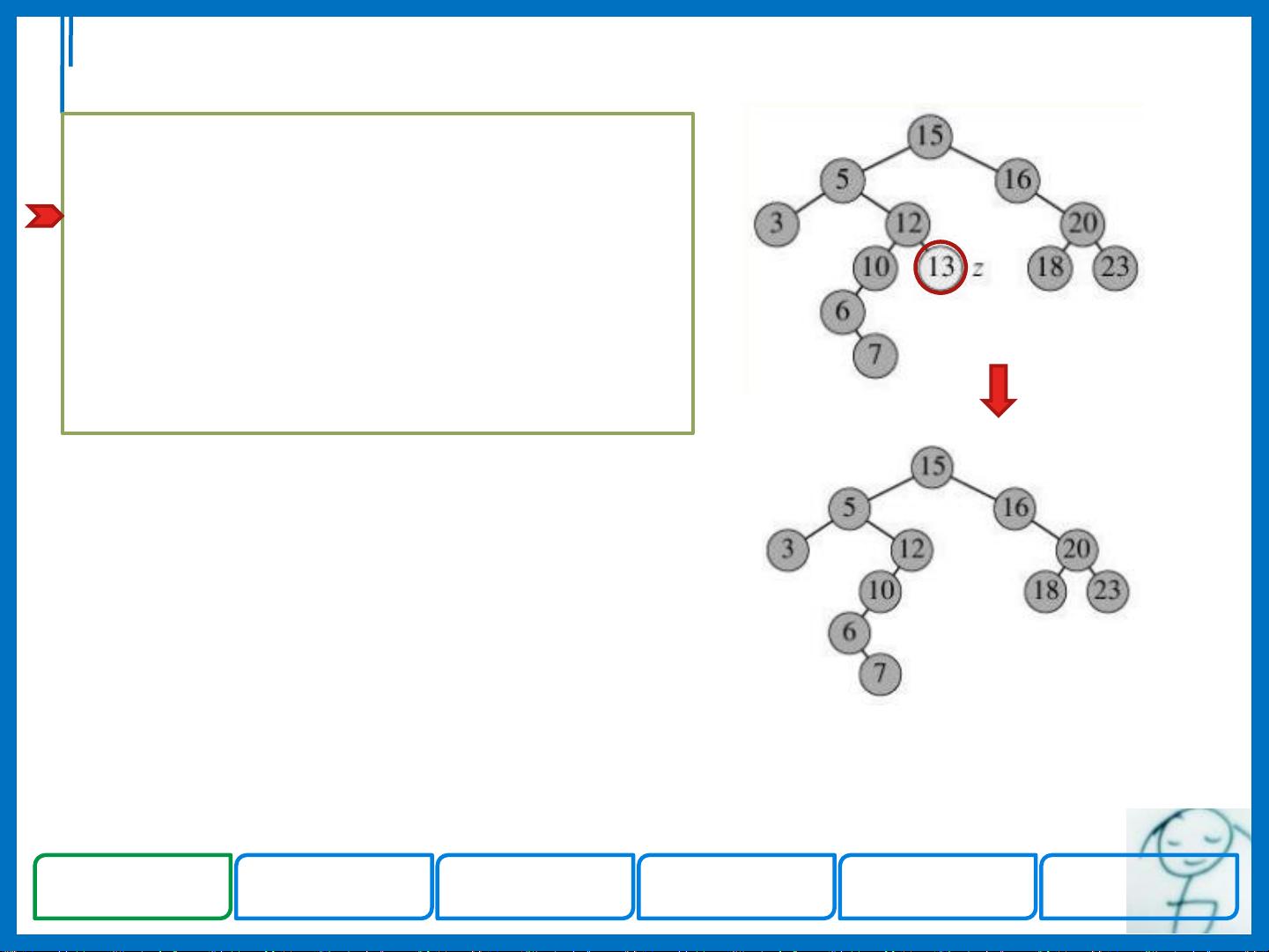 - **删除**：删除节点可能涉及到颜色调整和旋转操作，以确保红黑树的性质不被破坏。 - **旋转**：旋转用于在调整树结构时保持红黑树的平衡，包括左旋和右旋。例如，当插入一个新节点导致其父节点变为红色时，可能需要进行一次或两次旋转来重新平衡树。 - **总结**：红黑树的关键在于通过局部平衡来保证全局的平衡性，即使得树的深度在最坏情况下也能保持较小，从而提高操作效率。 **应用与比较**： 红黑树广泛应用于各种数据结构和算法中，如关联数组、内存管理和数据库索引。相比AVL树（另一种自平衡二叉查找树），红黑树的旋转操作更简单，但在最坏情况下，AVL树的平衡性更好，可能导致红黑树的性能略逊一筹。然而，在实际应用中，由于红黑树的插入和删除操作更快，因此通常更受欢迎。 红黑树是一种在保证查找效率的同时，通过牺牲严格的平衡性来简化插入和删除操作的数据结构。理解并熟练掌握红黑树的原理和操作对于任何从事计算机科学或软件工程的人来说都是至关重要的。