火星探测车的运动学模型与轨迹控制

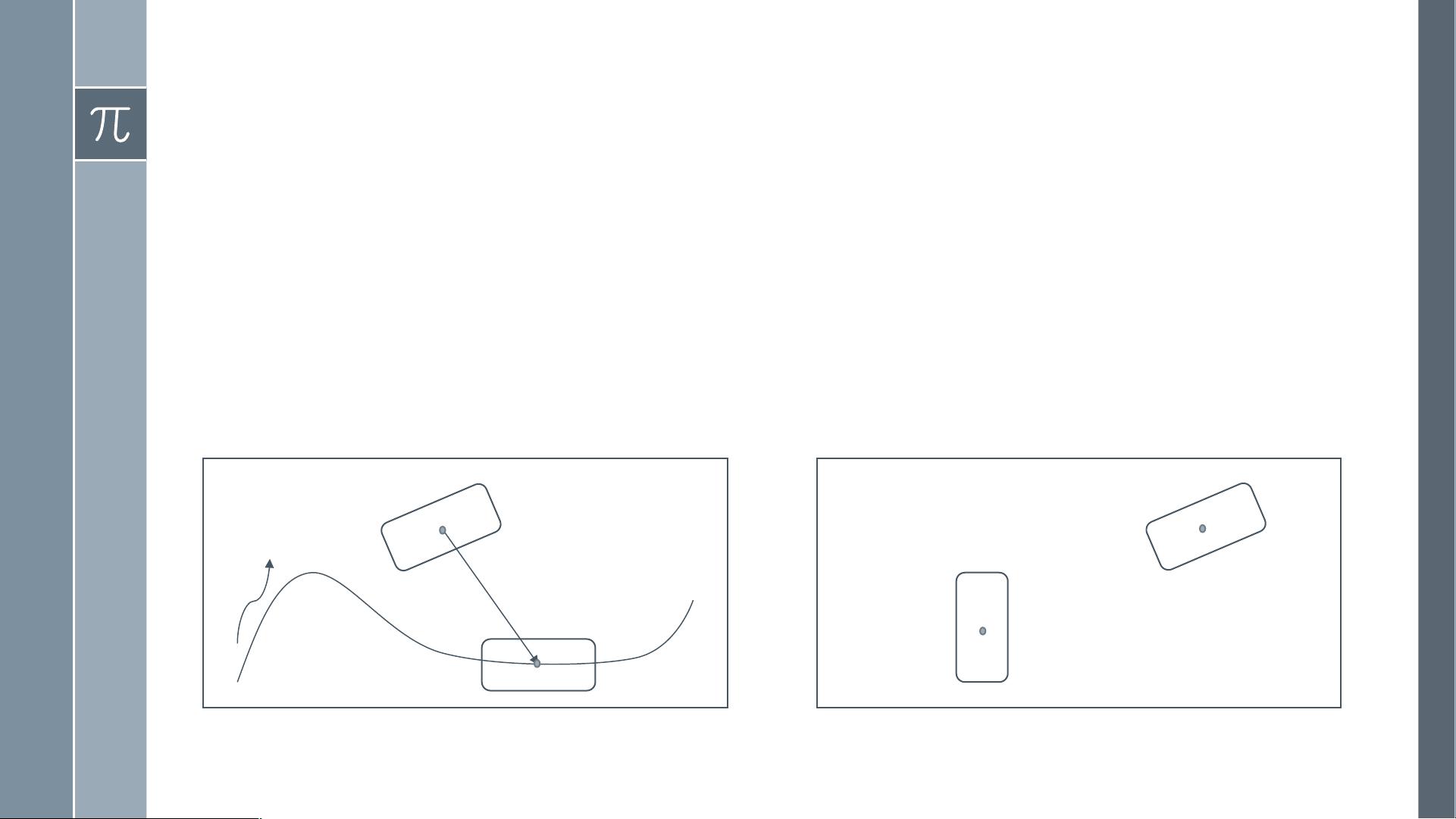
"独轮车的状态空间模型分析" 在机器人技术领域，状态空间模型是一种用于描述和控制复杂系统动态行为的数学工具。本资源聚焦于独轮车这一特殊类型的移动机器人，探讨其状态空间模型在轨迹跟踪、姿态调整以及运动控制中的应用。独轮车以其独特的平衡机制和灵活性，被广泛研究于各种探索任务，如火星探测。 火星探测车的历史始于1996年的火星探路者号，其携带的"索杰纳"号火星车开启了人类对火星表面的近距离探索。后续的探测任务如勇气号、机遇号、凤凰号和好奇号，都携带了各种高级仪器，如MastCam、MAHL、MARDI、SAM、ChemCam和CheMin，以进行详细的地质分析和环境研究。 独轮车的运动学模型在惯性坐标系下被建模，描述了车辆如何在期望轨迹上渐进移动。初始状态可能位于轨迹路径上也可能不在，但车辆必须能够精确调整其姿态以达到目标状态。轨迹跟踪是关键问题，因为它确保了车辆在有障碍的环境中安全、有效地执行任务。通过比较期望状态和实际状态之间的误差，可以设计控制器来纠正偏差。 控制理论中，通常采用近似线性化的方法设计轨迹控制器。这种方法假设动态误差在参考轨迹附近是小的，从而简化了控制问题。当误差减小时，线性化的精度提高。系统能控性和能观性是保证控制器有效性的基础，前者意味着通过控制输入可以到达系统的任何状态，后者则表示可以通过测量输出重建系统状态。 状态空间模型的表示形式为一系列矩阵，包括状态矩阵A、输入矩阵B和误差矩阵e。这些矩阵描述了系统动态和控制输入如何影响状态变量的变化。通过优化这些参数，可以设计出能够减少跟踪误差的控制器，实现精确的轨迹跟踪和姿态调整。 总结来说，独轮车的状态空间模型提供了一种理论框架，用于理解和控制这种独特机器人在复杂环境下的动态行为。通过对模型的近似线性化和误差反馈，可以设计出高效、精准的控制策略，确保在火星探索这样的任务中实现预期的轨迹跟踪和姿态控制。这一模型和方法不仅适用于火星探测车，也在其他领域的单轮或多轮机器人设计中具有重要的应用价值。