斐波那契数列计算器设计与电路实现

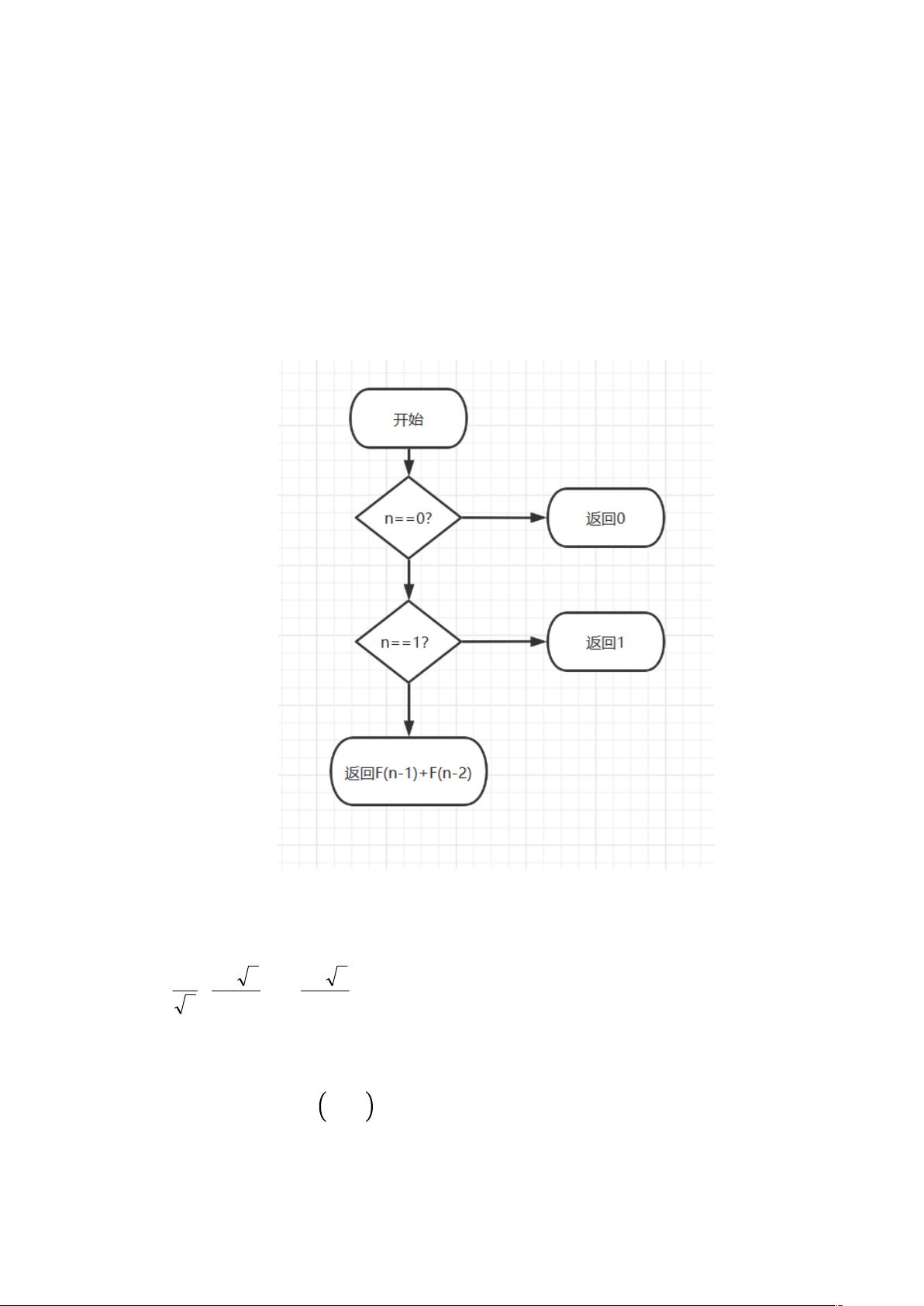
"实验6-CS1806-U201814788-刘美1: 斐波那契数列计算器设计" 斐波那契数列是一种经典的数学序列，其中每个数字是前两个数字的和。在本实验中，重点涉及了两种不同的算法来计算斐波那契数列：一种是递归算法，另一种是多项式时间复杂度的算法。 1. **斐波那契数列的通项公式**: 斐波那契数列的通项公式可以通过矩阵的形式表示为\( F_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n - (\frac{1-\sqrt{5}}{2})^n] \)，其中\( F_n \)表示第n项斐波那契数。 2. **递归算法**: 递归算法的定义是\( F_n = F_{n-1} + F_{n-2} \)，当\( n = 1 \)或\( n = 2 \)时，基础情况是\( F_1 = 1 \)且\( F_2 = 1 \)。然而，这种算法的时间复杂度是指数级的，即\( O(2^n) \)，因为它会进行大量的重复计算。 3. **多项式时间复杂度算法**: 提供的伪代码是一种优化的迭代方法，通过循环从第5项开始逆向计算到第0项，避免了递归中的重复计算。时间复杂度为线性，即\( O(n) \)。在这个算法中，变量`Start`和`X`被初始化，然后根据输入的二进制数组`n[i]`更新`X`，最终返回结果`X`。 4. **控制和显示部分设计**: - **左移控制部分**：使用移位寄存器加载初始值`n`，并通过clear和clock的逻辑组合确保在正确时刻加载。 - **clk控制电路**：借助8位计数器和比较器，确保只提供6个clock脉冲给fibo模块。比较器输出与clock信号结合，防止多余的脉冲传递给fibo模块。 - **锁存器**：利用锁存器在接收到n的最高位时将start信号设置为1，并保持该状态直至下次clear脉冲到来。 5. **主模块的Logisim电路图**: 在Logisim软件中，设计了一个包含上述控制和计算部分的电路，并进行了仿真验证，确保其基本正确性。这个电路图展示了如何将硬件逻辑与斐波那契数列计算的算法相结合。 通过这样的设计，实验旨在让学生理解不同算法的时间复杂度差异以及如何用硬件电路实现特定的计算任务，同时锻炼了他们的逻辑设计和验证能力。