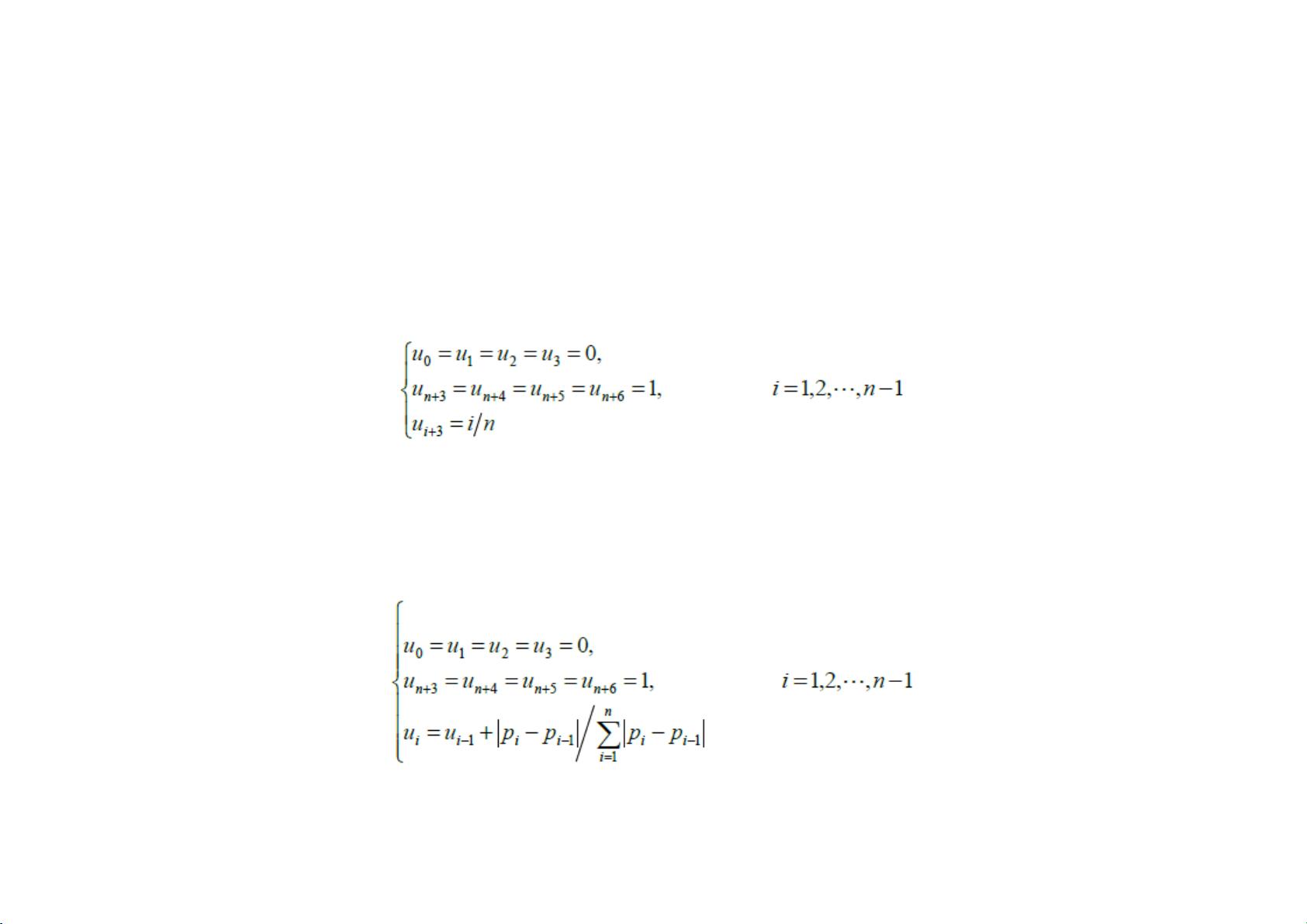NURBS曲线插值:Matlab编程实现与反求控制点解析
需积分: 25 125 浏览量
更新于2024-07-09
7
收藏 456KB PDF 举报
"这篇文档是关于通过给定一组数据点反求控制点的NURBS曲线插值生成的Matlab编程实例。文档包含了NURBS曲线的理论基础、计算过程和具体的Matlab实现,适用于学习和理解NURBS曲线的构建方法。"
NURBS曲线是一种强大的几何造型工具,它在工程领域广泛应用,特别是在三维建模和计算机图形学中。NURBS曲线具有灵活性和精确性,可以通过调整控制点和权因子来改变曲线形状,同时支持规则和自由曲面的表示。NURBS曲线的表达式是基于有理分式,其中包含了控制顶点、权因子和由节点矢量计算得到的B样条基函数。
在NURBS曲线方程中,权因子和控制顶点共同决定曲线形状,而节点矢量则影响B样条基函数的定义。对于开曲线,通常设定首尾节点的重复度以确保曲线的平滑性。当权因子不为零时,曲线的首末端点与控制多边形的对应顶点重合,并在这些点上与控制边相切。
NURBS曲线的插值问题分为两个主要类型:正算和反算。正算问题涉及已知控制点来求解曲线上的点,而反算问题则是给定一组型值点,反向计算出生成这条曲线所需的控制点。反算过程通常包括三个步骤:
1. 计算节点矢量:这一步骤确定了曲线的结构,节点矢量中的元素u_i决定了B样条基函数的分布。
2. 确定边界条件:根据型值点的位置和要求的曲线特征(如开曲线或闭曲线),设定合适的边界条件,以确保NURBS曲线能正确通过型值点。
3. 反算控制顶点:在已知节点矢量和边界条件的基础上,通过数值方法或迭代算法反向求解控制顶点,使得NURBS曲线能够精确地通过给定的型值点。
在Matlab编程实例中,这些概念和计算过程会被具体实现,提供了一种实践NURBS曲线插值的方法。通过阅读文档和运行源代码,学习者可以更深入地理解NURBS曲线的构造和应用,这对进行几何建模和曲线拟合非常有帮助。
为了提高效率,可能需要考虑优化算法的选择和数据结构的设计,比如采用更有效的搜索和插值方法,以及利用Matlab的内置函数和向量化操作。此外,文档可能还会讨论如何处理特殊情况,如自由端点的处理和曲线光滑性的保证。
这个Matlab编程实例为学习者提供了一个实用的平台,以便他们能够掌握NURBS曲线的基本原理,并将这些知识应用到实际问题中。通过实际操作,学习者可以更好地理解和运用NURBS曲线在几何造型和数据插值中的强大功能。
356 浏览量
892 浏览量
421 浏览量
379 浏览量
421 浏览量
1425 浏览量
892 浏览量
137 浏览量
626 浏览量
wikisoft
- 粉丝: 2
最新资源
- Premiere Pro CS6视频编辑项目教程微课版教案
- SSM+Lucene+Redis搜索引擎缓存实例解析
- 全栈打字稿应用:演示项目实践与探索
- 仿Windows风格的AJAX无限级树形菜单实现教程
- 乐华2025L驱动板通用升级解决方案
- Java通过jcraft实现SFTP文件上传下载教程
- TTT素材-制造1资源包介绍与记录
- 深入C语言编程技巧与实践指南
- Oracle数据自动导出并转换为Excel工具使用教程
- Ubuntu下Deepin-Wine容器的使用与管理
- C语言网络聊天室功能详解:禁言、踢人与群聊
- AndriodSituationClick事件:详解按钮点击响应机制
- 探索Android-NetworkCue库:高效的网络监听解决方案
- 电子通信毕业设计:简易电感线圈制作方法
- 兼容性数据库Compat DB 4.2.52-5.1版本发布
- Android平台部署GNU Linux的新方案:dogeland体验