掌握树与二叉树基础：算法与表达式转换

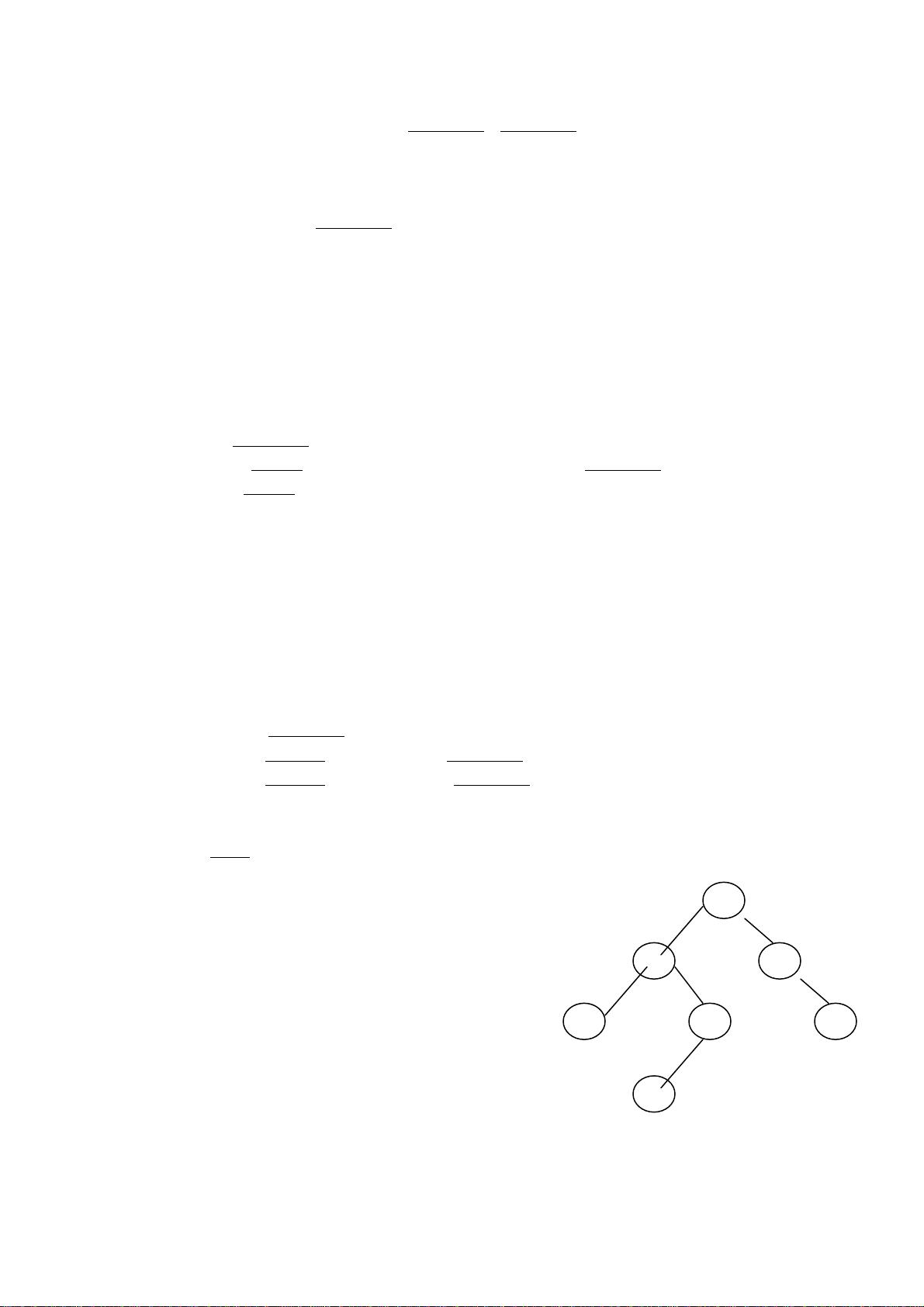
在本课程中，我们将深入探讨树和二叉树这一关键的数据结构概念。树是一种非线性数据结构，由一个根节点以及连接各个节点的边组成，每个节点可以有多个子节点，形成一种层次结构。二叉树则是特殊的树，每个节点最多有两个子节点，通常标记为左子节点和右子节点。 1. 选择题部分展示了树和二叉树在算法中的应用，例如算术表达式的前缀、后缀和中缀表示之间的转换。前缀表示法（Prefix Notation）中操作符写在操作数之前，如题目中的例子，理解这种转换对于解析和计算表达式至关重要。 2. 第二个问题涉及将算术表达式转换为后缀表达式（Postfix Notation），这是一种将运算符置于操作数之后的表示方式，便于计算机处理。正确答案应包含运算符优先级和结合性的规则，这有助于确保表达式的正确计算。 3. 对于第三题中的二叉树，理解二叉树的构造及其表示的算术表达式是解答的关键。通过观察二叉树的结构，可以推断出其对应的算术表达式是括号和运算符的组合，正确的选项会根据树的结构来组织算术运算。 4. 第四个问题涉及树的特性，特别是度数（子节点数）与叶子节点（没有子节点的节点）的关系。根据题目给出的节点度数分布，可以利用公式来计算叶子节点的数量，这里需要用到树的性质，即度为1的节点数等于所有节点数减去度大于1的节点数。 5. 选择题中的第五个结论考察了二叉树的基本性质，如二叉树的定义、度数限制和不同类型的二叉树（如完全二叉树和满二叉树）的比较。正确答案指出，二叉树的根节点度数可能是0或2，并且深度相同的情况下，完全二叉树的节点数少于或等于满二叉树。 6. 第六个问题是关于森林与二叉树的映射，森林是由多棵树构成的集合，而对应二叉树的问题中，确定森林中第一棵树的节点数需要考虑二叉树的结构特征，即根节点的子节点个数与整个二叉树的节点数之间的关系。 7. 最后一段进一步明确了树的定义，包括根节点的存在、子节点集合的划分以及度的概念。同时，区分了二叉树和一般的树，强调了二叉树的特殊性——只有一个根节点，并且提到二叉树的另一个特性——所有节点在同一层的子节点数量差不超过1时，称为平衡二叉树或AVL树。 通过这些选择题，学习者不仅可以掌握树和二叉树的基本概念，还能锻炼算法分析和逻辑思维能力，为后续的编程和数据结构学习打下坚实的基础。