时间序列分析:预测利器与方法详解
需积分: 50 101 浏览量
更新于2024-07-17
收藏 2.05MB PPTX 举报
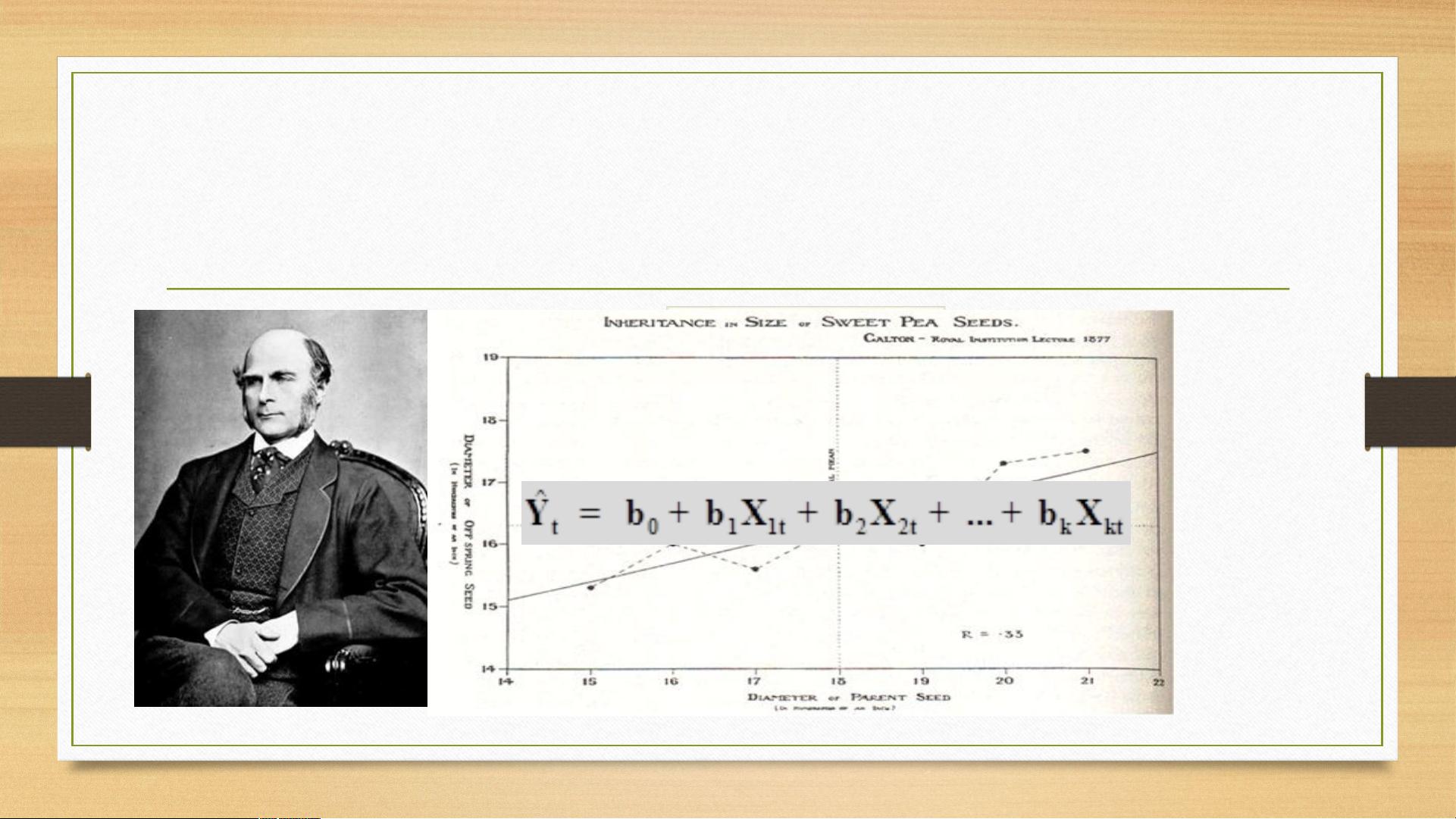
时间序列分析是一种统计学中的关键方法,用于处理和理解现象或统计指标随时间变化的数据模式。它通过将这些数据按照时间顺序组织成序列,为预测未来趋势提供了基础。时间序列分析的核心在于理解数据中的信号与噪声成分,并运用多种模型来捕捉数据的动态特征。
在时间序列分析中,重要的是假设数据可以分解为信号(表示可预测的模式)和噪声(不可预测的随机波动)。基本的方法包括:
1. **均值模型(Mean Model)**: 这是最简单的预测模型,假设序列的当前值仅依赖于一个常数斜率(Ŷt = α)。
2. **线性趋势模型(Linear Trend Model)**: 建立在时间变量上,预测值由一个固定斜率和一个时间项(Ŷt = α + βt)组成。
3. **随机步长模型(Random Walk Model)** 和 **几何随机游走模型(Geometric Random Walk Model)**: 随机步长模型假设当前值等于前一值加一个随机误差,而几何随机游走模型则是对对数数据应用随机步长模型。
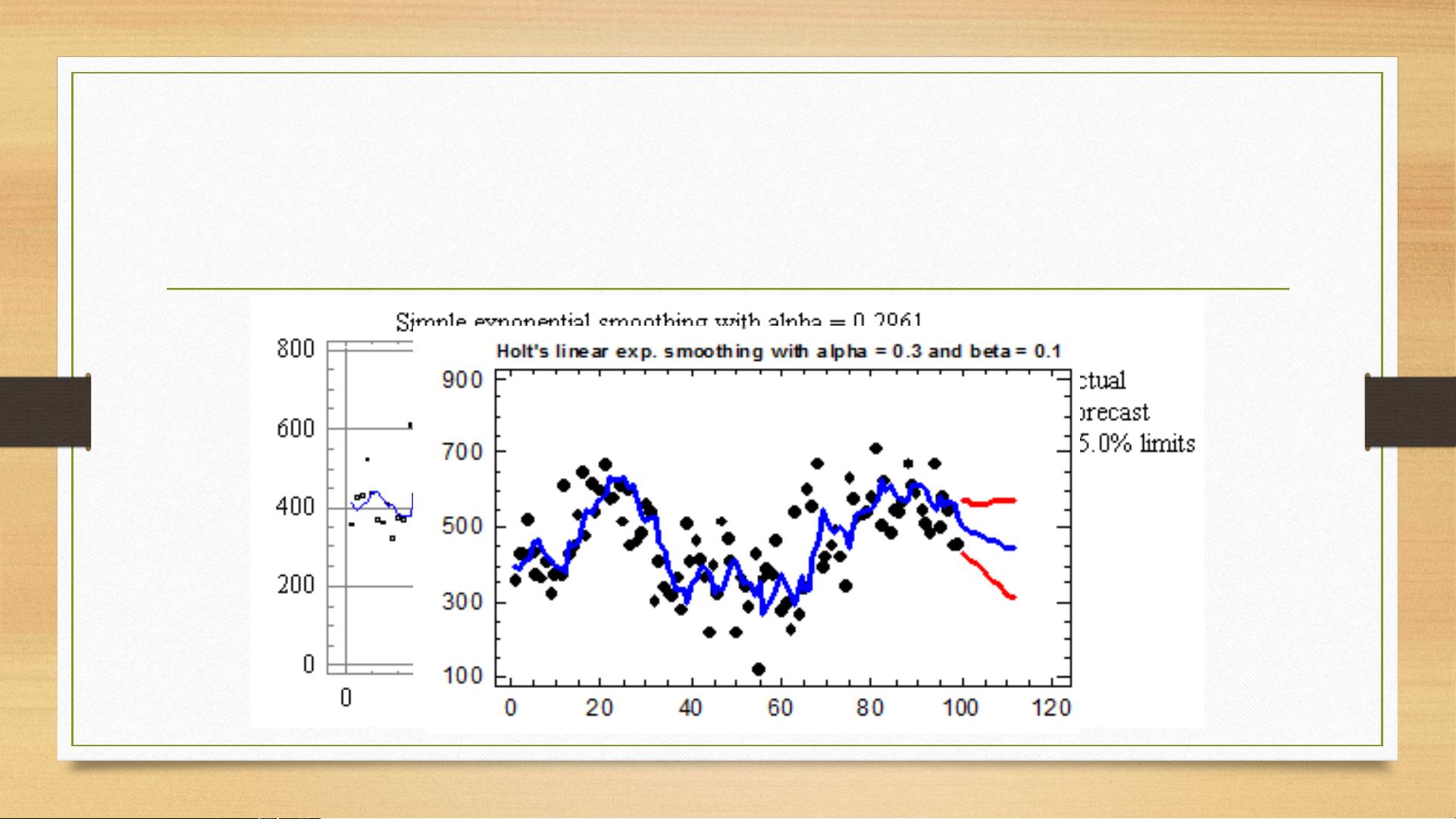
4. **简单移动平均模型(Simple Moving Average Model)** 和 **布朗指数平滑模型(Brown's Simple Exponential Smoothing Model)** 及 **Holt指数平滑模型(Holt's Linear Exponential Smoothing Model)**:移动平均方法利用历史数据点的加权平均来预测未来值。
5. **阻尼线性趋势指数平滑模型(Damped Trend Linear Exponential Smoothing Model)**: 在线性趋势模型中加入了衰减因子,以控制长期趋势的稳定性。
6. **自回归移动平均模型(ARIMA)**: 一种更为复杂的模型,ARIMA(1,1,2)是其一个实例,它结合了自回归(AR)、差分(I)和移动平均(MA)概念,能够处理非平稳序列,使之变得平稳以便建模。
ARIMA模型,如ARIMA(1,0,0)和ARIMA(0,2,1),分别代表一阶自回归和无常数的线性指数平滑,是Box-Jenkins模型的重要组成部分。这种模型能够考虑序列的季节性影响,为季节性时间序列提供准确的预测。
在实际应用中,时间序列分析的关键步骤是确保数据的平稳性,即数据的均值、方差和自相关性在时间上保持不变。这是因为在建立模型时,需要依赖历史数据来反映未来趋势,而如果这些统计特性随时间变化,预测结果可能会失真。因此,预处理数据以达到平稳性是时间序列分析的必要前提。
2018-02-20 上传
2009-04-13 上传
2011-07-12 上传
2021-09-28 上传
2018-05-16 上传
weixin_40911987
- 粉丝: 0
- 资源: 4
最新资源
- Chrome ESLint扩展:实时运行ESLint于网页脚本
- 基于 Webhook 的 redux 预处理器实现教程
- 探索国际CMS内容管理系统v1.1的新功能与应用
- 在Heroku上快速部署Directus平台的指南
- Folks Who Code官网:打造安全友好的开源环境
- React测试专用:上下文提供者组件实现指南
- RabbitMQ利用eLevelDB后端实现高效消息索引
- JavaScript双向对象引用的极简实现教程
- Bazel 0.18.1版本发布,Windows平台构建工具优化
- electron-notification-desktop:电子应用桌面通知解决方案
- 天津理工操作系统实验报告:进程与存储器管理
- 掌握webpack动态热模块替换的实现技巧
- 恶意软件ep_kaput: Etherpad插件系统破坏者
- Java实现Opus音频解码器jopus库的应用与介绍
- QString库:C语言中的高效动态字符串处理
- 微信小程序图像识别与AI功能实现源码