线段树详解：杨弋讲稿

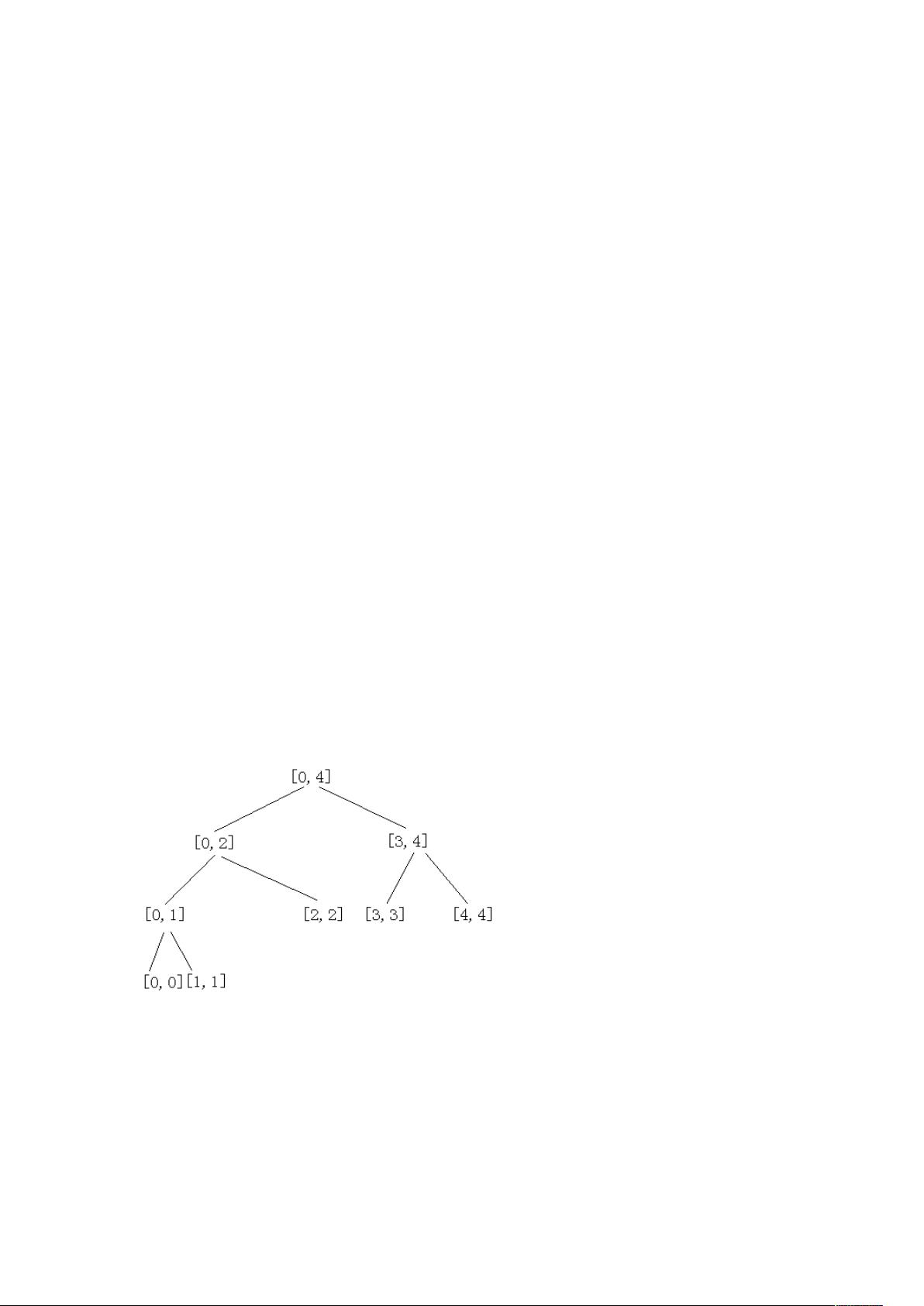
线段树是一种高效的数据结构，常用于处理区间查询和区间更新的问题，尤其在ACM/ICPC竞赛编程中广泛应用。杨弋线段树讲稿详细讲解了线段树的基本概念、构建方法以及操作流程。 线段树的核心在于它是一棵完全二叉树，其中每个节点代表一个区间或线段。线段树的根节点表示整个数组或序列的区间，而其左右子节点分别表示原区间的一半。通过递归地将区间分割，线段树可以在O(log n)的时间复杂度内完成对区间信息的查询和修改。 以RMQ（Range Minimum Query）问题为例，线段树可以用来查找数组中一段连续子序列的最小值。在构建线段树的过程中，每个节点不仅存储其对应区间的边界，还会维护这个区间内的最小值。初始化时，如果节点对应的区间只包含一个元素，那么该节点的最小值就是这个元素。接着，将区间一分为二，递归地为左右子节点构建子树，并更新父节点的最小值为左右子节点最小值的较小者。 线段树的修改操作也非常直观。若要修改某个元素的值，只需从根节点开始，通过比较目标位置与当前节点覆盖的区间，决定向左子树还是右子树继续递归。当找到覆盖目标位置的叶子节点时，更新该节点的值。由于线段树的分治特性，这个过程同样能在O(log n)时间内完成。 除了基本的最小值查询和修改，线段树还可以扩展实现区间加减、求和等操作。通过在节点中存储区间和或者其它统计信息，线段树可以灵活应对各种区间操作的问题。 线段树的存储空间优化也是关键。虽然原始线段树需要O(2n)的空间，但可以通过压缩存储，例如使用懒惰标记策略，来减少不必要的空间开销，达到O(n)的存储需求。 线段树是解决动态区间问题的强大工具，它提供了快速查询和修改区间信息的能力，且结构简单，易于理解和实现。在实际应用中，如数据分析、实时计算等领域，线段树都有广泛的应用。通过深入理解和掌握线段树，开发者能够更有效地处理大量数据的区间操作，提升算法效率。