ADC的非线性分析：DNL与INL计算原理

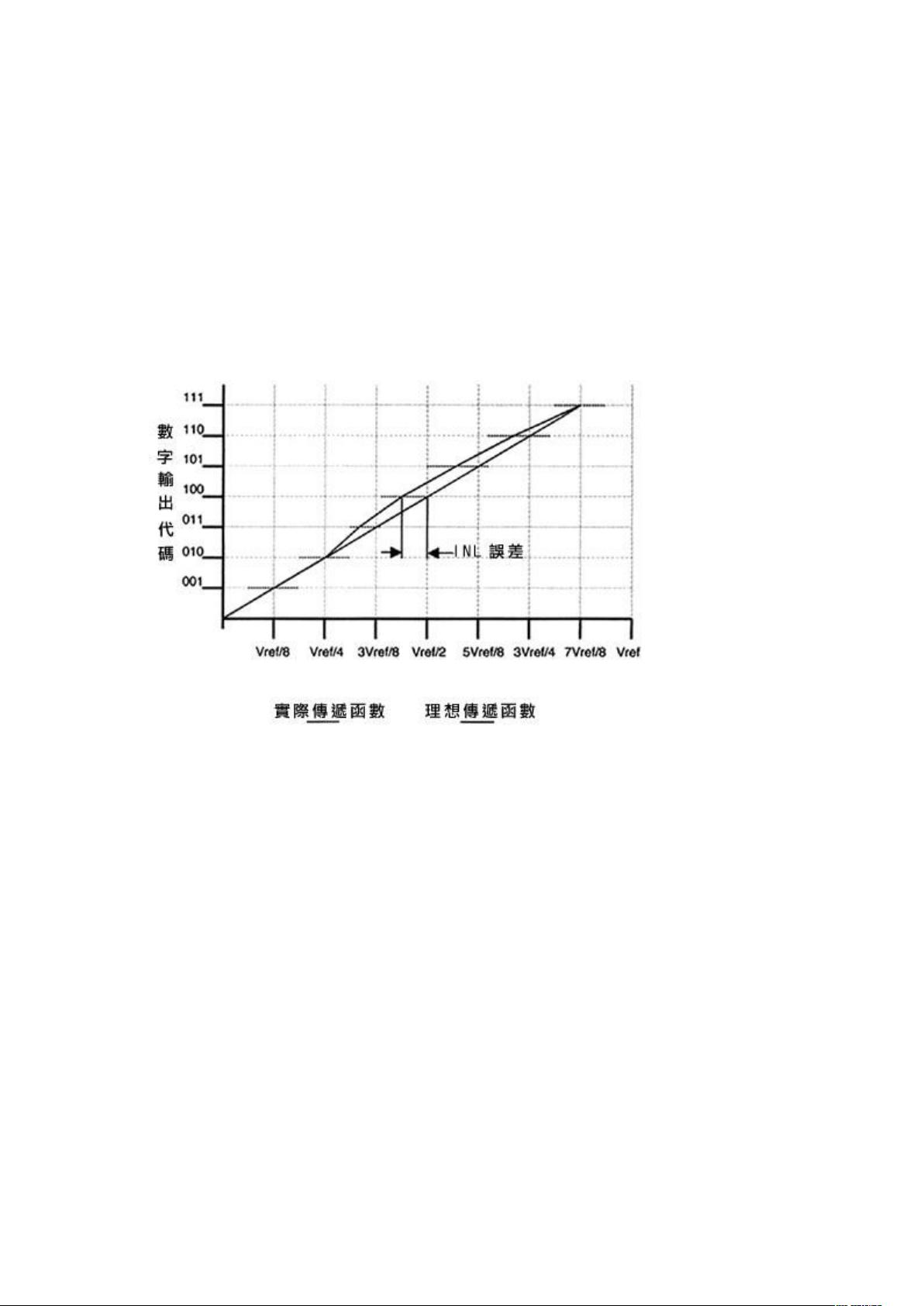
"DNL INL的计算方法与理解" 积分非线性（Integral Nonlinearity，INL）和差分非线性（Differential Nonlinearity，DNL）是评估模数转换器（ADC）性能的重要指标，尤其关乎其转换精度。ADC在将模拟信号转换为数字信号时，其输出序列应尽可能接近理想线性关系，但实际中总会存在一定的误差。 DNL衡量的是相邻输出代码之间的误差，即实际步距与理想步距的差异。如果DNL始终为正或始终为负，表示转换过程中存在恒定的偏移，这种情况下ADC的输出可能会出现跳跃或缺失的代码。DNL的理想值是0，意味着每个输出代码间的步距都与理论值相等。DNL的单位通常是最小可分辨步长（Least Significant Bit，LSB）。 INL则是DNL的积分形式，它反映了在整个转换范围内，输出代码与理想线性关系的最大偏差。一个具有优秀INL的ADC意味着其DNL误差被有效地平均或分散，从而使得整体的非线性误差最小。INL的计算是通过累计所有DNL误差的结果，以LSB为单位表示。 计算DNL和INL的方法有很多种。传统的代码平均和电压抖动法虽然可行，但随着ADC位数增加，计算所需时间会显著增长。因此，直方图法成为了一种更高效的选择，特别是线性斜升直方图法。这种方法通过逐渐改变输入电压并记录输出代码的出现频率（点击数）来分析非线性误差。 在直方图法中，输入电压线性增加，ADC输出的每个代码出现的次数（点击数）代表了对应输入电压范围的大小。点击数越多，说明非线性微分误差越大；反之，点击数越少，误差越小。例如，如果某个代码的理想点击数为8，但实际上达到9次，那么DNL误差为(9-8)/8或0.125 LSB。INL则是所有DNL误差的累加，对于斜升直方图，就是每个DNL误差的总和。 通过统计分析直方图数据，可以精确计算出ADC的DNL和INL，从而全面了解其线性性能。这些参数对于高精度测量、通信系统和其他依赖ADC准确转换的应用至关重要。因此，理解和优化ADC的DNL和INL对于提高系统整体性能是十分必要的。