"图的概念、存储结构、遍历、生成树、最短路径和拓扑排序 | 数据结构-71"

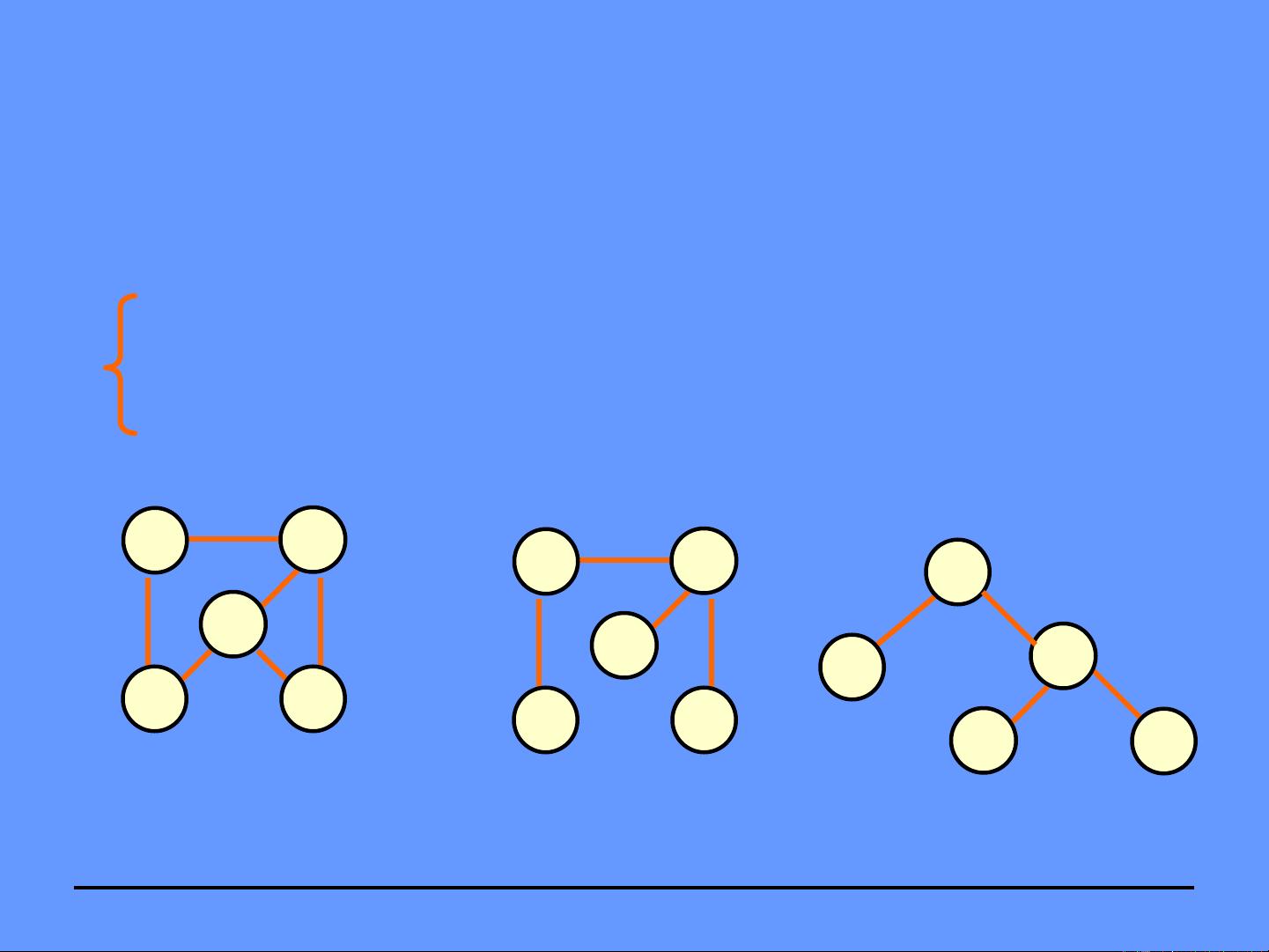
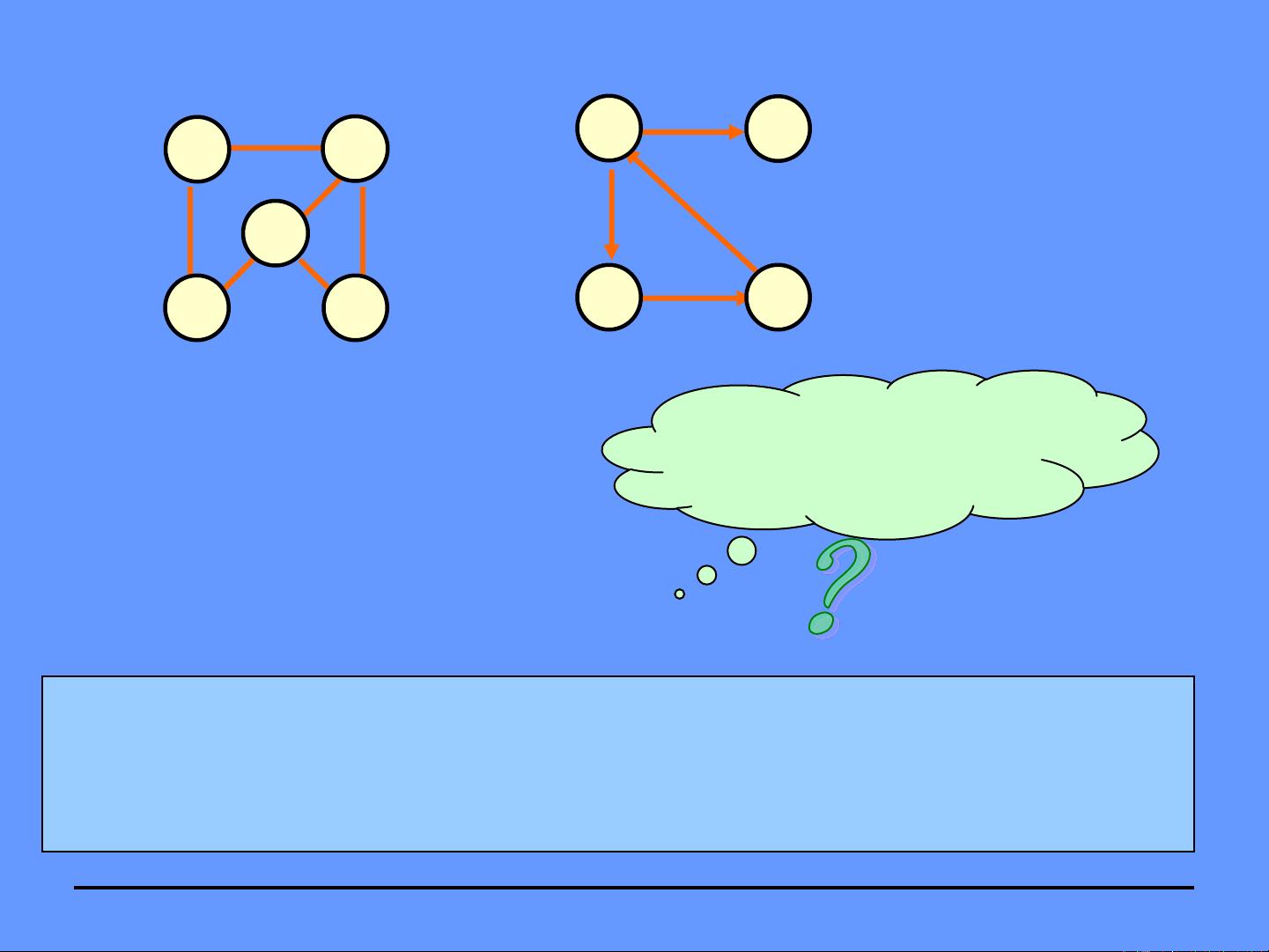
本章主要介绍了图的概念、存储结构、遍历、生成树、最短路径和拓扑排序等内容。图是一种多对多的结构关系，其中每个元素可以有零个或多个直接前趋和零个或多个直接后继。本章的学习要点包括熟悉图的各种存储结构及其构造算法，了解实际问题的求解效率与采用何种存储结构和算法有密切联系；熟练掌握图的两种遍历算法：深度优先遍历和广度优先遍历。在学习中需要注意图的遍历算法与树的遍历算法的差异。 图的概念是本章的起点，图是由顶点集合和边集合组成的一种数据结构，顶点可以表示某个实体，边可以表示实体间的关系。在图中，顶点之间可以有直接连接的边。图可以用来模拟各种实际问题，如社交网络、电路等。 图的存储结构是图的内部表示方式，常见的图的存储结构包括邻接矩阵和邻接表。邻接矩阵是一个二维数组，其中的元素表示边的存在与否；邻接表使用链表来表示顶点之间的连接关系。不同的存储结构适用于不同的问题，选择适当的存储结构能够提高问题的求解效率。 图的遍历是指访问图中所有顶点的过程。深度优先遍历和广度优先遍历是两种常用的图遍历算法。深度优先遍历从起始顶点开始，一直访问其未访问过的相邻顶点，直到无法继续访问为止。广度优先遍历则按照层级顺序访问顶点，先访问第一层级的顶点，再访问第二层级的顶点，以此类推。深度优先遍历适用于查找路径和连通性等问题，而广度优先遍历适用于最短路径和拓扑排序等问题。 生成树是一种特殊的图，它是原图中的一个子图，包含了原图所有顶点和部分边，并且不包含回路。生成树可以用来表示最小代价的连通图，常用的生成树算法包括Prim算法和Kruskal算法。 最短路径是指两个顶点之间的最短路径，它可以通过图中的边的权值来表示。最短路径算法包括Dijkstra算法和Floyd算法。Dijkstra算法适用于求解单源最短路径问题，而Floyd算法适用于求解所有顶点之间的最短路径。 拓扑排序是对有向无环图进行排序的过程，排序结果满足图中的边的方向。拓扑排序算法包括深度优先搜索和宽度优先搜索。拓扑排序在工程、设计和计算等领域有着广泛的应用，如任务调度、作业排序等。 总的来说，本章介绍了图的概念及其存储结构，以及图的遍历、生成树、最短路径和拓扑排序等算法。对于理解和应用图的基本概念和算法有着重要的意义。通过学习本章内容，可以掌握图相关算法的思想和实现方法，为解决实际问题提供了一种有效的数据结构和算法工具。