量化大规模MIMO系统：基带天线数与ADC分辨率的优化
164 浏览量
更新于2024-08-28
收藏 1.96MB PDF 举报
"Low-Cost Massive MIMO: Pilot Length and ADC Resolution"
在无线通信领域，大规模多输入多输出（Massive MIMO）系统是提高频谱效率和能量效率的关键技术。然而，实现这样的系统通常需要大量的硬件资源，尤其是高分辨率的模拟数字转换器（ADC）。本文探讨的是在设计低成本、能源高效的Massive MIMO系统时，如何处理基站（BS）天线数量和ADC分辨率这两个相互冲突的参数。
文章指出，在采用低分辨率ADC的情况下，每个接收天线的性能会受到影响，这直接影响到系统的整体性能。研究重点在于量化Massive MIMO系统中天线数量与ADC分辨率的联合优化问题，特别是在不完美的信道状态信息（CSI）条件下。作者们提出了一个可解析的近似上行链路总谱效率（Sum Spectral Efficiency, SE）表达式，该表达式基于最大比合并（Maximal Ratio Combining, MRC）接收机。通过这个表达式，他们进一步提出了一种优化的导频长度，以最大化系统的总SE。
考虑到ADC的影响，文章提供了一个现实的总功率消耗模型。利用这个模型，研究人员建立了选择BS天线数量的优化问题，旨在平衡系统性能与能耗之间的关系。这个问题的解决对于实现真正意义上的低功耗、大规模部署的Massive MIMO网络至关重要。
文章中，作者们可能采用了数学建模和仿真分析的方法，探讨了不同天线数量和ADC分辨率组合下的系统性能，并可能给出了最佳配置的指导原则。此外，他们还可能讨论了在有限的导频序列下，如何有效地估计信道并减小由于CSI不准确带来的影响。
这篇研究论文对于理解在有限资源约束下如何优化大规模MIMO系统的设计提供了有价值的见解，特别是对于那些希望在保持高效能的同时降低设备成本的通信工程师和研究人员而言。其结果有助于推动未来无线通信网络的可持续发展，特别是在5G及更高级别的网络中，低功耗和高效率是关键设计目标。
16 Journal of Communications and Information Networks
section VI summarizes the main conclusions of this paper.
Notations: Throughout the paper, boldfaced letters are used
to represent vectors and matrices. The operator (·)
H
and (·)
∗
stand for the Hermitian and conjugate of a matrix, respec-
tively. We let I
N
denotes an N × N identity matrix, and
diag(A) denotes the diagonal matrix with the same diago-
nal elements as matrix A. The notation E
{
·
}
indicates the
expectation operator, whereas
k
·
k
stands for the Euclidean
norm. We use C N (·,·) to denote a multi-variate circularly-
symmetric complex Gaussian distribution.
II. SYSTEM MODEL
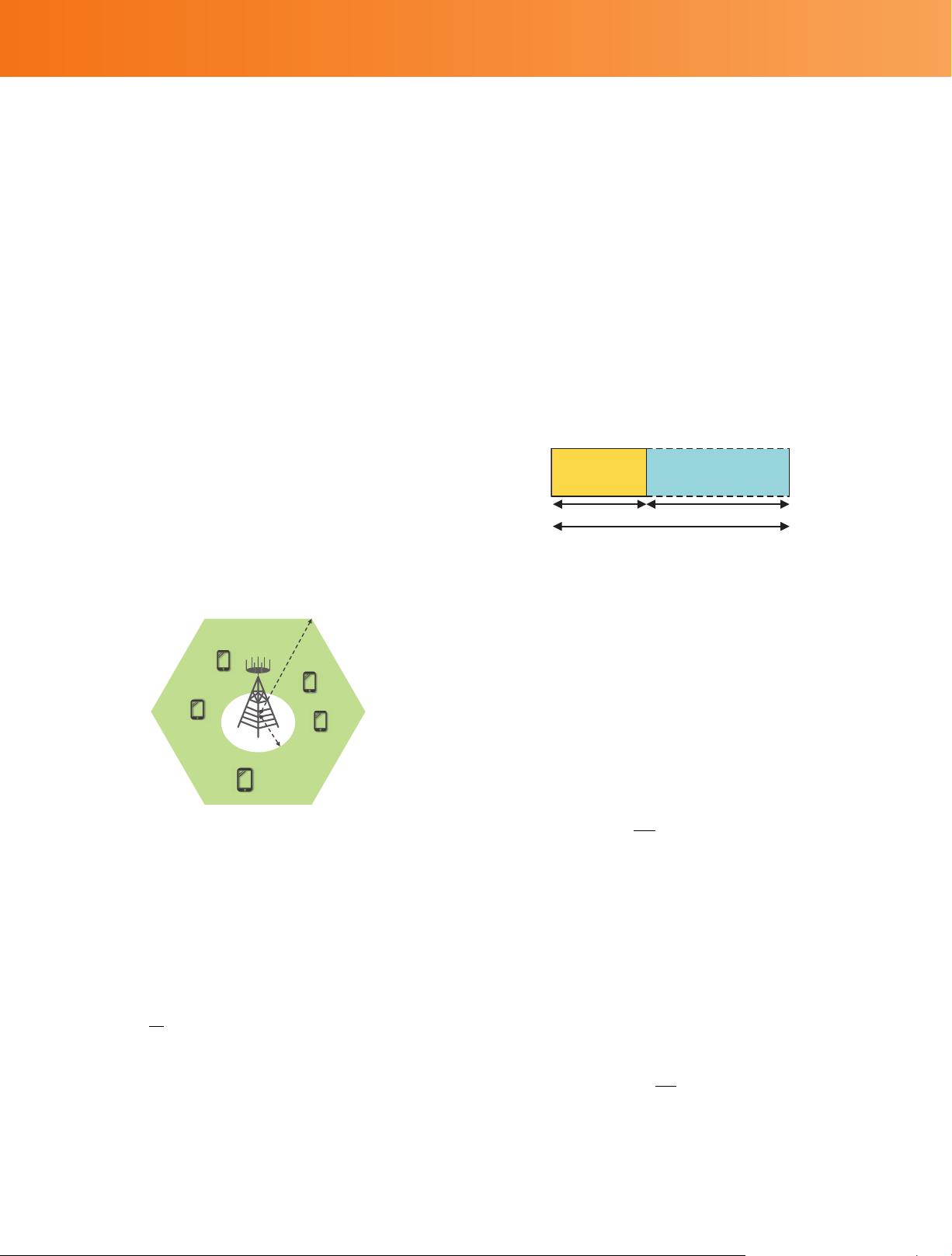
Consider the uplink of a single-cell multi-user MIMO sys-
tem formed by a base station (BS) equipped with an array of
M antennas and serving N single antenna user terminals in
the same time-frequency resource (see Fig. 1). The hexag-
onal cell is assumed to have radius of r
c
, and the users are
distributed uniformly and randomly over it with the exclusion
of a central disk of radius r
h
. We assume independent and
identically distributed (i.i.d.) Rayleigh block fading over T
symbols, which means that the channels are considered static
within each time-frequency coherent block and have indepen-
dent realizations in different blocks.
r
c
r
h
Figure 1 Illustration of a multi-user MIMO scenario: a BS is equipped with
an array of M antennas and simultaneously serves N randomly distributed
single-antenna user terminals in the same time-frequency resource
Single-carrier, narrowband transmission is considered, and
thus the channel matrix between BS and users are represented
by an M ×N matrix G = HD
1/2
, where H is the M ×N
matrix modeling small-scale fading coefficients between the
users and BS, and D is the N ×N diagonal matrix represent-
ing the large-scale fading (both path loss and shadow fad-
ing) coefficients. The (m, n) element of G can be modeled as
g
mn
= h
mn
p
β
n
, with h
mn
describing the instantaneous prop-
agation channel from the nth user to the mth antenna of BS
and β
n
being the large-scale fading component. We assume a
Rayleigh small-scale fading distribution such that h
mn
is zero
mean, circularly symmetric, complex Gaussian random vari-
able with variance 1. Besides, β
n
is assumed to be constant
across the antenna array
[13]
.
Linear processing is used at a BS to perform uplink data
detection. Under imperfect CSI assumption, the UEs send
orthogonal pilot sequences of length τ symbols to the BS
for channel estimation, which indicates that (T −τ) symbols
are left to enable uplink data transmission. The entire uplink
transmission process consists of the following three phases.
• First, the UEs send pilot sequences which are spatially
orthogonal and τ symbols long. As seen from Fig. 2, uplink
pilot transmission takes place first and occupies τ symbols.
• Second, based on the received pilot sequences at the BS,
channel estimation is performed for linear receiver processing.
In this paper, we ignore the processing time needed for this
phase.
• Third, all terminals send their uplink data to the BS using
the remaining (T −τ) symbols, which is shown in Fig. 2.
uplink pilot
uplink
transmission
τ symbols (T − τ) symbols
coherent time: T symbols
Figure 2 Illustration of the uplink transmission: uplink pilot signaling takes
place first and occupies τ symbols; the subsequent (T −τ) symbols are used
for uplink data transmission
A. Uplink Training and Data Transmission
In the uplink training phase, the UEs transmit a sequence
of pilot signals which can be grouped into a matrix Ψ =
[ψ
1
,··· ,ψ
i
,··· ,ψ
N
] ∈ C
τ×N
with each element ψ
n
= [ψ
n
] ∈
C
τ×1
being the pilot vector for the nth user and τ represent-
ing the number of training symbols. Assuming that each user
terminal transmits the pilot symbol with equal transmit power
p
t
, the signal of ith symbol at the receive antennas z
i
∈ C
M×1
is written as
z
i
=
√
τ p
t
N
∑
n=1
ψ
ni
g
n
+ w
i
, (1)
where g
n
denotes the nth column of the channel matrix G,
ψ
ni
is the ith element of ψ
n
, and w
i
represents the additive
white Gaussian noise (AWGN) vector with zero mean and unit
element-wise variance written as w
i
∼ C N (0, I
M
).
In practical systems, an automatic gain control (AGC) vari-
able gain amplifier is usually used before the ADC to adjust
the dynamic range of the received signal z
i
. We assume the
gain of AGC is set appropriately, and by adopting the additive
quantization noise model, the output of the quantizer can be
formulated as
ˆz
i
= αz
i
+ ˆw
i
= α
√
τ p
t
N
∑
n=1
ψ
ni
g
n
+ αw
i
+ ˆw
i
, (2)
where α = 1 −ρ with ρ being the inverse of the signal-to-
quantization-noise ratio, and ˆw
i
is the additive Gaussian quan-
剩余13页未读，继续阅读
108 浏览量
158 浏览量
295 浏览量
2021-02-07 上传
189 浏览量
199 浏览量
118 浏览量
165 浏览量
1331 浏览量
