the radio-over-fiber 共RoF兲 method 共described in Sec. VI兲 can
use optical fibers to deliver THz modulated optical signals to
the exterior of buildings before converting to free space THz
radiation. As THz sources and detectors are developed for
communication, THz waveguides may fill a critical role in
the coupling of radiation between THz components.
B. Directionality of THz radiation
The importance of the diffractive effects in free-space
THz systems can be explored using the Friis formula. Fol-
lowing the analysis of Brown,
41
the power supplied to the
load of the receiving antenna is given by
P
out
= P
in
冉
4
d
冊
2
G
r
G
t
F
r
共
r
,
r
兲F
t
共
t
,
t
兲
p
, 共1兲
where P
in
is the input power to the transmitting antenna, G is
the antenna gain, F is the normalized intensity pattern func-
tion,
is the path power transmission factor,
p
is the polar-
ization coupling efficiency, is the wavelength of the radia-
tion, and d is the distance between the transmitting 共t兲 and
receiving 共 r兲 antenna. The angles
and
refer to spherical
coordinates at either the receiver or transmitter. The free-
space loss factor 共 / 4
d兲
2
arises from two effects: 共1兲 The
assumption that the receiving antenna is detecting the far-
field radiation of the transmitting antenna leads to treating
the source as emitting a spherical-like wave whose power
decreases as 1/ d
2
with distance. 共2兲 The factor of
2
arises
from the diffraction limited directivity 共D
max
兲 or alternatively
the solid angle which defines the extent of the diffracting
intensity pattern function such as: D
max
=4
/ ⍀ =4
A
eff
/
2
,
for which A
eff
is the effective area of the detector.
The antenna gain and directivity are related by
G
t
=
P
rad
P
in
D
t
, 共2兲
where P
rad
is the power radiated by the antenna. If we as-
sume that the radiation and input powers are matched, then
the gain of the antenna is equal to the directivity. In this case,
Eq. 共1兲 can be rewritten as
P
out
= P
in
A
t
A
r
d
2
2
F
r
共
r
,
r
兲F
t
共
t
,
t
兲
p
, 共3兲
where A
t
and A
r
refer to the effective areas of the transmitter
and receiver, respectively. According to Eq. 共3兲, the power
received at a detector varies as 1 /
2
so the efficiency of
detection improves as the wavelength decreases or the THz
frequency increases. This implies that THz communications
are inherently more directional than microwave or MMW
links due to less free-space diffraction of the waves. Conse-
quently, THz communication systems will typically be line-
of-sight systems.
Mann
25
used a simplified version of Eq. 共3兲 to estimate
the maximum data transmission distance of a 400 GHz ver-
sus a 60 GHz system. Despite the fact that THz sources are
currently less powerful than comparably sized microwave
sources, the maximum distances for data transmission
共⬃1.9–2.0 km兲 are comparable. The low power of a 400
GHz system is compensated by the fact that the 400 GHz
radiation diffracts less than 60 GHz radiation.
C. Scintillation
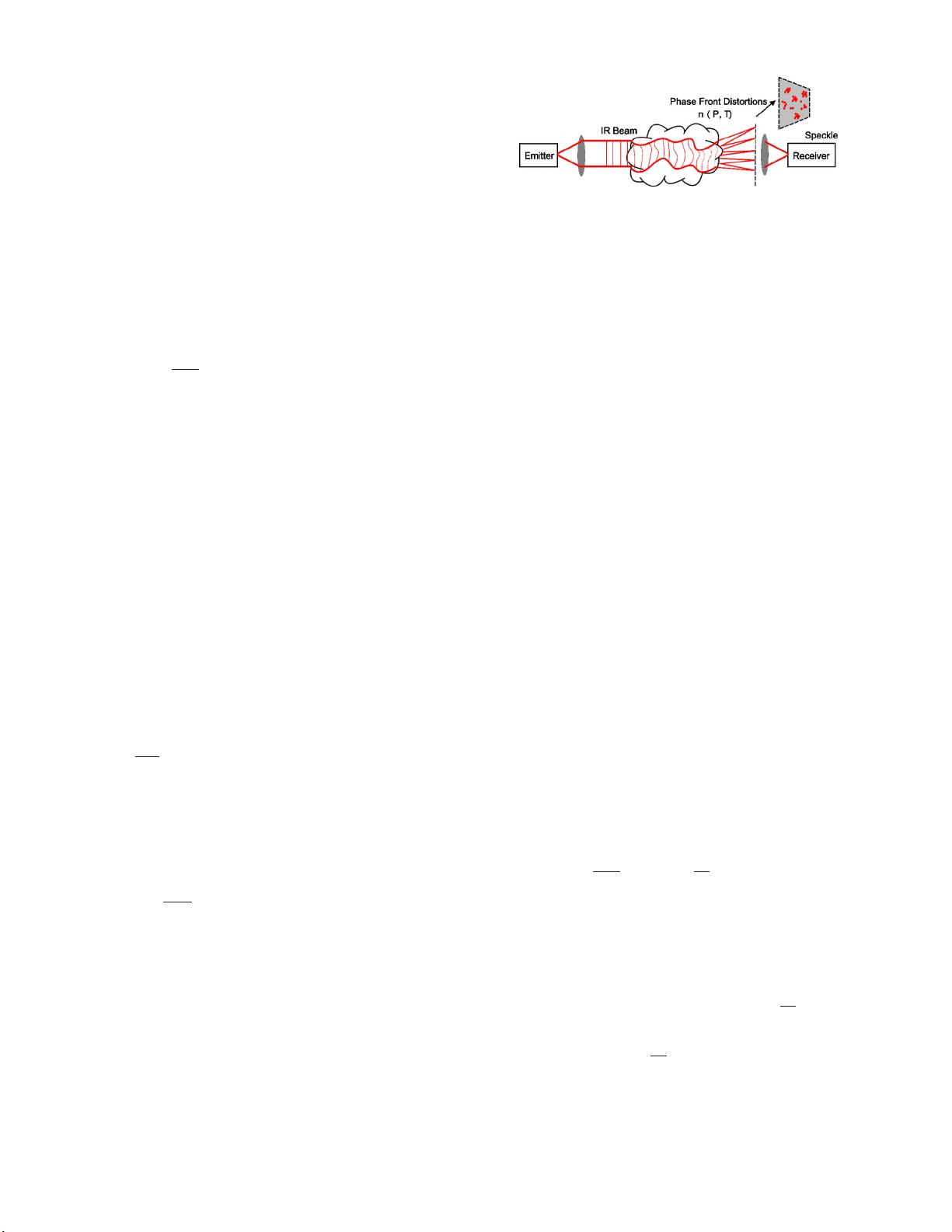
Real refractive index fluctuations can destroy the flat
phase front of an IR light beam when it passes a few kilo-
meters of air. Local temperature, pressure, or humidity gra-
dients, which are generated by thermals and turbulences near
ground level, cause small refractive index variations across
the wave front of the beam. Even if a single local refractive
index fluctuation only slightly distorts the wave’s phase
front, the effect can accumulate over a few kilometers of
propagation distance resulting into a complete or almost
complete destruction of the phase front. As a consequence,
on the receiver side the beam cross section appears as a
speckle pattern 共Fig. 1兲 with huge local and temporal inten-
sity variations preventing detection of constantly sufficient
signal power. In the absence of fog, these scintillation effects
are the main link length limitation in free-space IR commu-
nication systems. Complex equalizer schemes for phase front
correction based on mirrors arrays were proposed as counter
measure but could not show so far convincing performance.
As will be discussed below, THz beams are much less sus-
ceptibly to scintillation compared to IR beams.
The refraction index of air in the millimeter wave band
up to a few hundred gigahertz can be well approximated as
function of temperature and pressure by
n
mmW
⬇ 1+
7.76
T
冋
P
a
+ 4810
P
v
T
册
⫻ 10
−6
, 共4兲
where T, P
a
, P
v
stand for the temperature in kelvin, the at-
mospheric pressure in kilopascal, and the water vapor pres-
sure in kilopascal, respectively.
42
Similarly, for IR wave-
lengths the refraction index of air can be written as:
n
IR
⬇ 1 + 7.76 ⫻ 10
−6
关1 + 7.52 ⫻ 10
−3
−2
兴
P
a
T
⬵ 1 + 7.76 ⫻ 10
−6
P
a
T
, 共5兲
where stands for the wavelength in micrometers.
43
The
formula does not consider humidity as it only insignificantly
degrades IR propagation. Under the assumption of relevant
air parameters a numerical comparison of both formulas
shows that even at high levels of water vapor pressure the
FIG. 1. 共Color online兲 Air turbulence causes refractive index fluctuations
resulting into speckle 共intensity variations at receiver兲 that limits the reach
of IR systems.
111101-4 J. Federici and L. Moeller J. Appl. Phys. 107, 111101 共2010兲
Reuse of AIP Publishing content is subject to the terms at: https://publishing.aip.org/authors/rights-and-permissions. Download to IP: 128.187.112.19 On: Tue, 12 Apr 2016
19:06:31










