Abstract—There usually exists a high density of traffic through
bottleneck sections of mainline railways, where a perturbation of
one single train could result in long consequential delays across a
number of trains. In the event of disturbances, rescheduling trains
approaching the bottleneck will be necessary to increase the
throughput of the section. To model the real time train
rescheduling problems around bottleneck sections, a Mixed
Integer Programming model is presented in this paper. An
innovative improved algorithm (DE_JRM) is developed to solve
the problem. The model and the algorithms are validated with a
case study using Monte Carlo methodology, which demonstrates
that the proposed algorithm can reduce the Weighted Average
Delay and satisfy the requirements of real time traffic control
applications.
Index Terms—Train rescheduling, Railway Traffic
Management, Differential Evolution, Bottleneck section.
I. INTRODUCTION
s the passenger and freight transport volume increase
throughout Europe, many mainline railways have been
experiencing a high density of railway traffic, resulting in
services being very susceptible to minor delays and
disturbances, especially in the sections where different services
converge from a range of origins and diverge to a variety of
destinations. These sections can be called “bottleneck
sections”. Generally there are two junctions located at either
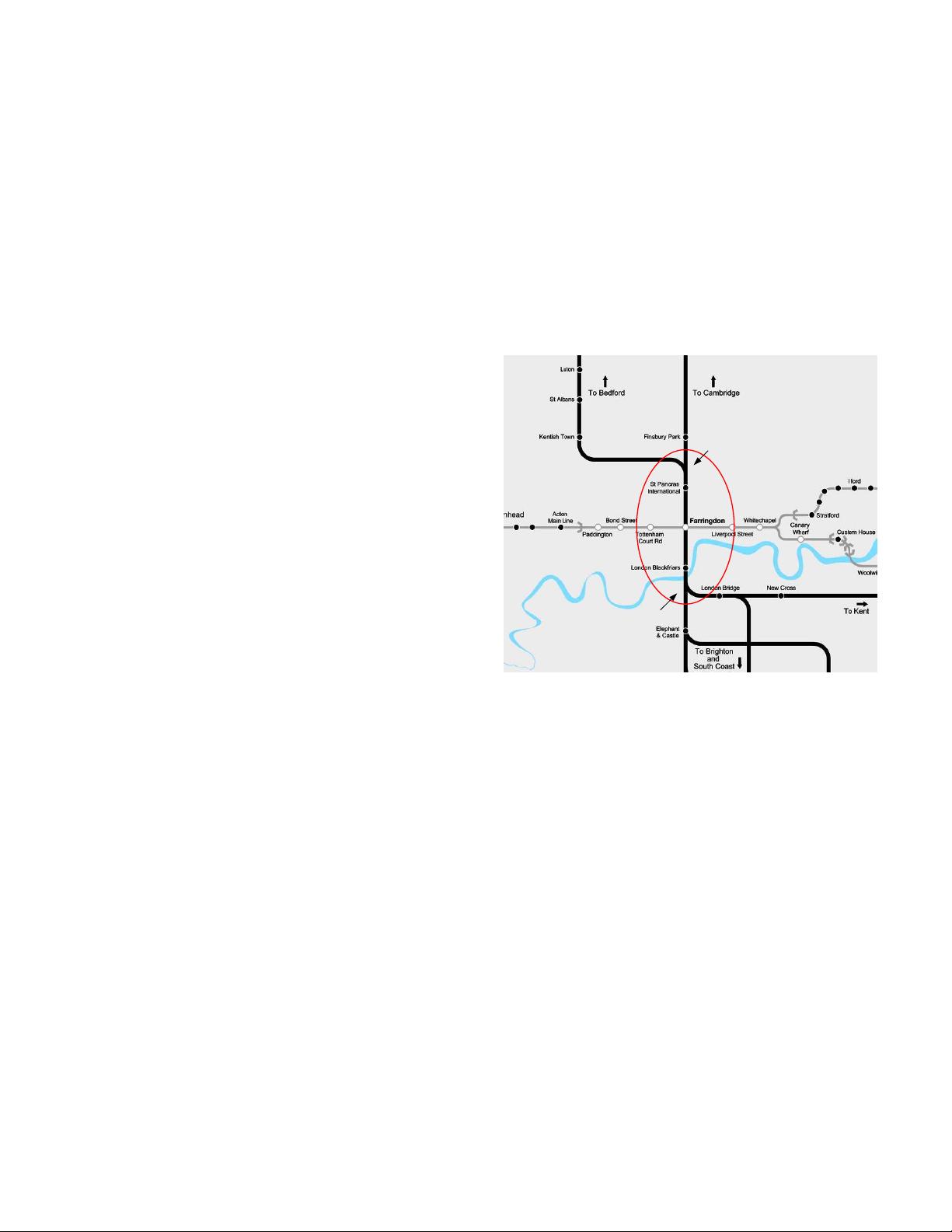
end. A typical example is the Core Area of the Thameslink
Route in London, UK as shown in Fig. 1. Due to the very high
density of traffic through bottleneck sections, the train
headways are relatively small, thus the allowance times and
buffer times added in the original nominal timetables are
insufficient to absorb train delays caused by unexpected
disruptions that occur in daily railway operations. A relatively
small perturbation to one train may cause long knock-on delays
for following trains on the same route and merging trains on
Manuscript received on 26
th
June 2014, and accepted on 2
nd
December 2014.
This work is supported by European Commission Framework Program 7
project ON-TIME, and the grant from the National Natural Science Foundation
of China (61304185).
L. Chen, C. Roberts and E. Stewart are with the School of Electronic,
Electrical and Computer Engineering, The University of Birmingham,
Edgbaston, Birmingham B15 2TT UK (e-mail: l.chen.3@ bham.ac.uk).
F. Schmid is with the School of Civil Engineering, The University of
Birmingham, Edgbaston, Birmingham B15 2TT UK (e-mail: f.schmid@
bham.ac.uk).
other routes, because of resource conflicts created by crossing
moves and the necessary signal overlaps.
Core Area of
Thameslink Route
Portal Junction
Portal Junction
Fig. 1. Sketch map of the Core Area of Thameslink Route in London, UK
(Websites of Network Rail)
To maintain a high quality of railway services in bottleneck
sections, train delays need to be well managed to reduce their
propagation. Therefore the trains approaching bottleneck
sections need to be rescheduled in an optimal manner to
minimize the overall delays following a disturbance, which is
regarded as a key requirement of the next generation of railway
traffic management systems [1-3].
In a bottleneck section there are generally two junctions
located at either end, these are referred to as known “portals”.
Approaching trains from different origins converge at the
bottleneck sections through the two portal junctions (arriving at
one portal junction and leaving from another one). In the
bottleneck sections, real time train rescheduling problems of
portal junctions need to simultaneously consider all entry/exit
points to the bottleneck. The rescheduling of approaching trains
for one portal junction needs, therefore, to consider the
movements of the trains approaching this portal junction from
another portal junction.
The authors of this paper will present a systematic
methodology of real time traffic management for bottleneck
sections including re-timing and re-sequencing of trains when
approaching the bottleneck sections. The mathematical model
Modeling and Solving Real Time Train
Rescheduling Problems in Railway Bottleneck
Sections
L. Chen, Member, IEEE, C. Roberts, Member, IEEE, F. Schmid and E. Stewart









