数据结构与算法:线性查找与折半查找解析
版权申诉
58 浏览量
更新于2024-07-02
收藏 2.46MB PDF 举报
"数据与算法课件:8 查找.pdf"
数据与算法是计算机科学的基础,其中查找技术是核心组成部分,用于在数据集中找到特定的信息。查找效率直接影响着程序的性能,因此各种查找算法的设计与优化至关重要。本课件主要讨论了查找表、哈希表和索引等概念。
6.1.1 到 6.1.4 节内容可能涵盖了查找的基本原理和线性查找。线性查找是最基础的查找方法,它遍历查找表中的每个元素,逐个比较关键字直到找到目标或遍历结束。线性查找的时间复杂度为O(n),其中n是查找表的长度。查找过程的效率可以通过计算平均查找长度(Average Search Length, ASL)来评估,ASL是查找过程中期望的关键字比较次数。
6.2 节可能涉及到了静态索引结构,这种结构适用于只读取数据的情况,不支持频繁的插入和删除操作。静态查找结构如数组,虽然查找效率较低,但结构简单且易于实现。
6.3.4 节可能提到了动态查找结构,如二叉查找树、B树、AVL树等,它们不仅能进行查找,还支持高效的插入和删除操作,适应数据集的变化。
6.6 和 6.7 节可能涵盖了更高级的查找技术,如图的表示、最小生成树和最短路径算法。这些内容在解决网络优化问题、路由选择和数据分发等方面有广泛应用。
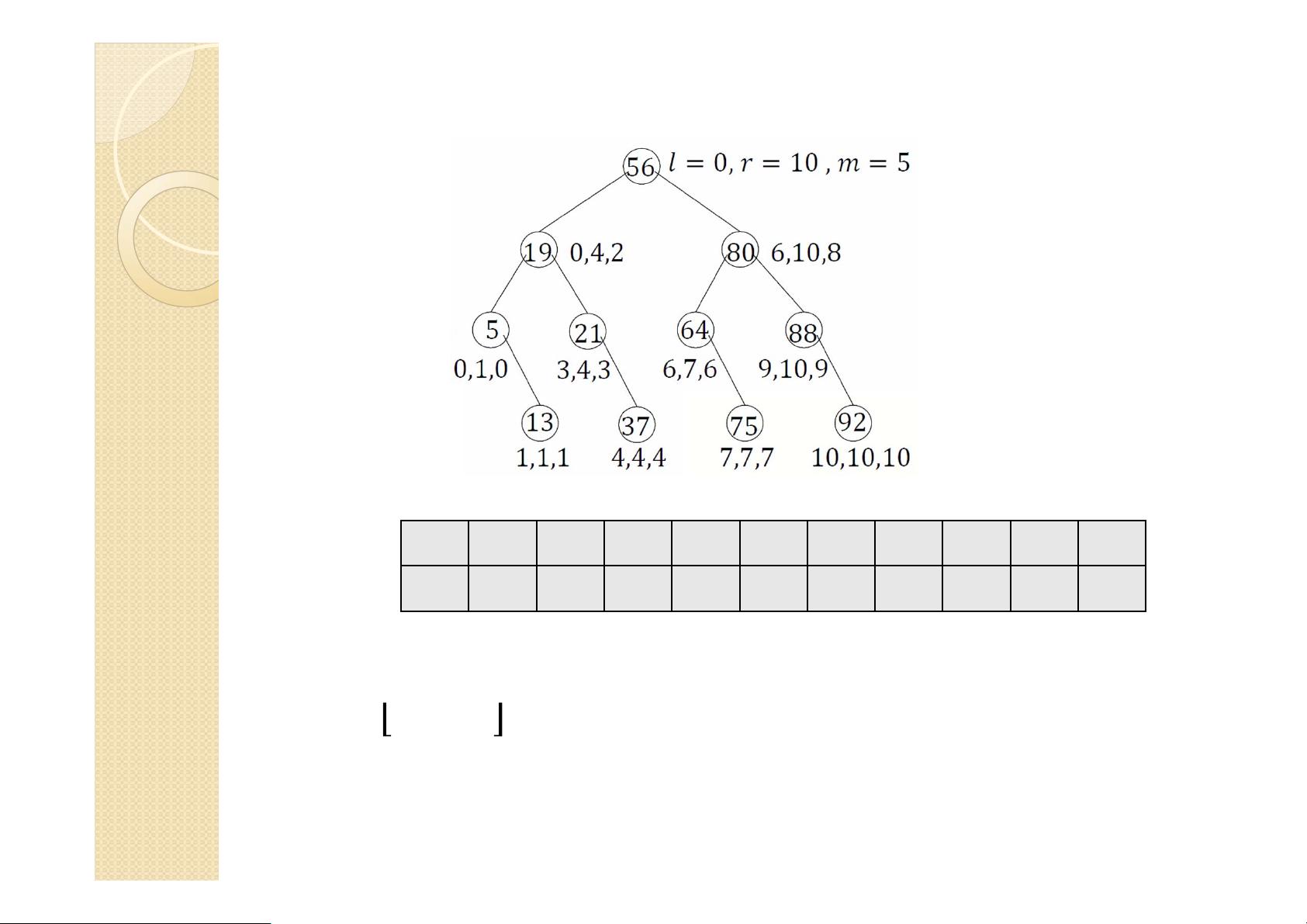
线性查找表的特点在于其简单性,但效率相对较低。例如,当在一个无序的线性查找表中查找目标时,平均需要比较n/2次关键字。如果表是有序的,可以使用折半查找(Binary Search)来提高效率,其时间复杂度为O(log n)。折半查找通过将查找范围不断减半来快速定位目标。
除此之外,哈希表(Hash Table)提供了另一种高效的查找方法,通过哈希函数将关键字映射到固定大小的存储空间,实现常数时间O(1)的查找、插入和删除操作,前提是哈希冲突较少。然而,解决哈希冲突会增加额外的复杂性。
查找技术在数据与算法的学习中占有重要地位,不同的查找方法各有优缺点,适用于不同的应用场景。理解并掌握这些查找算法,能够帮助我们设计出更高效的数据处理解决方案。
2022-06-26 上传
2022-06-26 上传
2022-06-26 上传
2022-06-26 上传
2022-06-26 上传
111 浏览量
2022-06-26 上传
131 浏览量
2022-06-26 上传
wxg520cxl
- 粉丝: 25
- 资源: 3万+
最新资源
- C语言实现对象编程之多态代码.rar
- HTML+Javascript轮播效果
- todolist-app
- dickinson:文本生成语言
- Kubernetes设置
- sourceloopup.zip
- 上海无纸记录仪 SPR90系列.zip
- bootstrap企业网站模板
- HyperNerd:用于监视和不和谐的全面监视自动禁止机
- onlineQuizGameWebsite:在线问答游戏网站
- simonx.github.io
- kettle(学习手册、中文手册、Kettle使用培训文档)
- 个人网站
- 自动泊车代码Matlab-499-dataset-analysis:499-数据集分析
- goodies
- lintcode:解决lintcode问题的方法