LINGO优化建模指南：从基础到应用

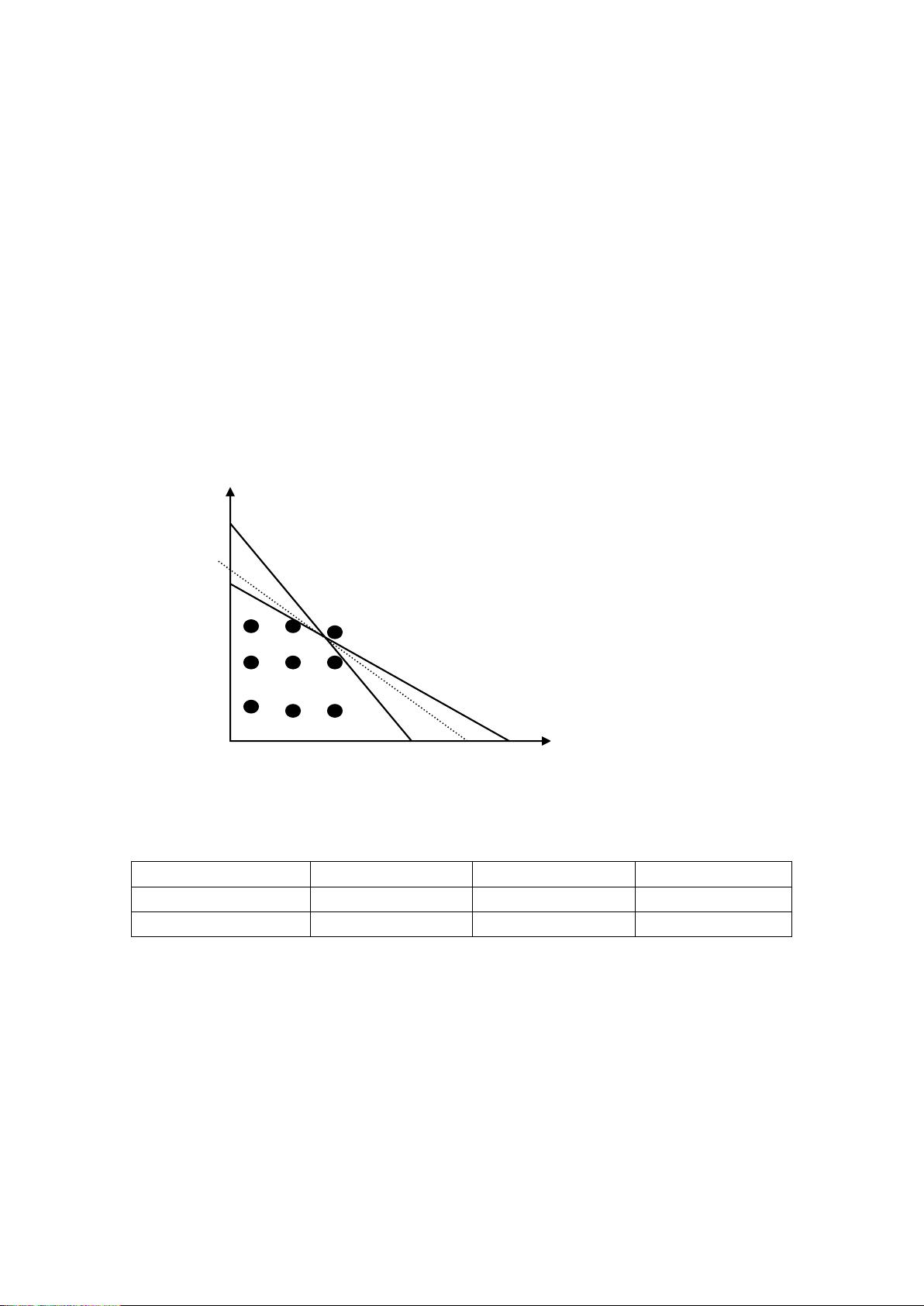
"LINGO教程大全" LINGO（Linear Interactive and General Optimization）是一款强大的数学建模软件，主要用于解决各种类型的优化问题，包括线性、非线性、整数和二次规划等。通过学习LINGO，你可以掌握如何用简洁的语法来构建复杂的数学模型，并将其转化为可求解的计算机程序。 在"第一章引言"中，教程首先介绍了优化模型的基本概念。这部分内容可能会涵盖以下几个关键点： 1. 优化模型的一般形式：优化模型通常涉及到寻找一个目标函数的最优值，这个目标函数在一组约束条件下被最大化或最小化。例如，目标函数可以是利润、成本、效率等，而约束条件可能涉及资源限制、生产量上限、市场需求等。 1.1.1 可行解与最优解：可行解是指满足所有约束条件的解，而最优解是所有可行解中使目标函数达到最好（最大或最小）的解。理解这一点是进行优化建模的基础。 1.1.2 优化模型的基本类型：LINGO支持多种类型的优化模型，包括： - 线性规划：目标函数和约束都是线性的，是最基础的优化模型。 - 二次规划：目标函数是二次函数，约束可以是线性的也可以是非线性的。 - 非线性规划：目标函数或约束包含非线性项，处理起来相对复杂。 - 整数规划：变量必须取整数值，常用于决策问题，如生产计划、资源分配等。 1.2 优化问题的建模实例：这部分将通过具体案例解释如何使用LINGO构建各种类型的优化模型。 1.2.1 线性规划模型：线性规划模型通常用于解决资源分配、生产调度等问题。通过定义决策变量、目标函数和线性约束，可以找到使总效益最大或最小的解决方案。 1.2.2 二次规划模型：二次规划在工程设计、投资组合优化等领域有广泛应用。模型的目标函数为二次函数，可以处理具有平方项的优化问题。 1.2.3 非线性规划模型：非线性模型处理含有非线性函数的目标函数或约束，如指数、对数、绝对值等。这些模型通常出现在物理、化学反应、经济学等领域。 1.2.4 整数规划模型：整数规划增加了变量只能取整数的限制，使得问题更加复杂。它在制造业、物流、项目管理等需要精确决策的场景中非常常见。 1.2.5 其他优化模型：除了上述模型，LINGO还支持其他类型的优化问题，如动态规划、随机规划、多目标优化等，这些模型分别适用于处理时间序列问题、不确定性环境和多目标冲突的情况。 通过学习LINGO教程大全，你将能够掌握优化理论的基本概念，学会如何使用LINGO工具进行模型构建、求解和分析，从而解决实际工作中的各种优化问题。教程可能还会涉及模型的求解方法、结果解读以及如何利用LINGO的高级特性来处理复杂问题。通过深入学习，你可以提升在数学建模和决策分析方面的能力。