信号处理仿真分析：学习曲线与权值演化

"该资源是何子述的《现代数字信号处理及其运用》第四章的仿真练习，由田改生完成。主要涉及信号处理中的学习算法，通过MATLAB代码展示了不同步长对最小均方误差（MSE）及权重更新的影响。" 在本资源中，我们看到的是一个关于信号处理的基础仿真案例，特别是针对学习算法的学习曲线和权重更新过程的分析。这里使用了LMST（Levenberg-Marquardt Steepest Descent，勒让德-马夸特最陡下降法）算法，这是一种结合了梯度下降法和牛顿法的优化方法，常用于非线性最小二乘问题。 1. **LMST算法**： LMST算法是一种迭代优化技术，主要用于求解最小化非线性函数的问题，特别是在数据拟合和参数估计中。在这个例子中，它被用来调整权重以减小均方误差（MSE）。 2. **步长参数**： 仿真中涉及到三个不同的步长参数，分别是0.015、0.025和0.05。步长决定了在每次迭代时权重更新的幅度。较大的步长可能会导致更快的收敛速度，但可能不稳定；较小的步长则可能导致更慢的收敛，但可能更稳定。 3. 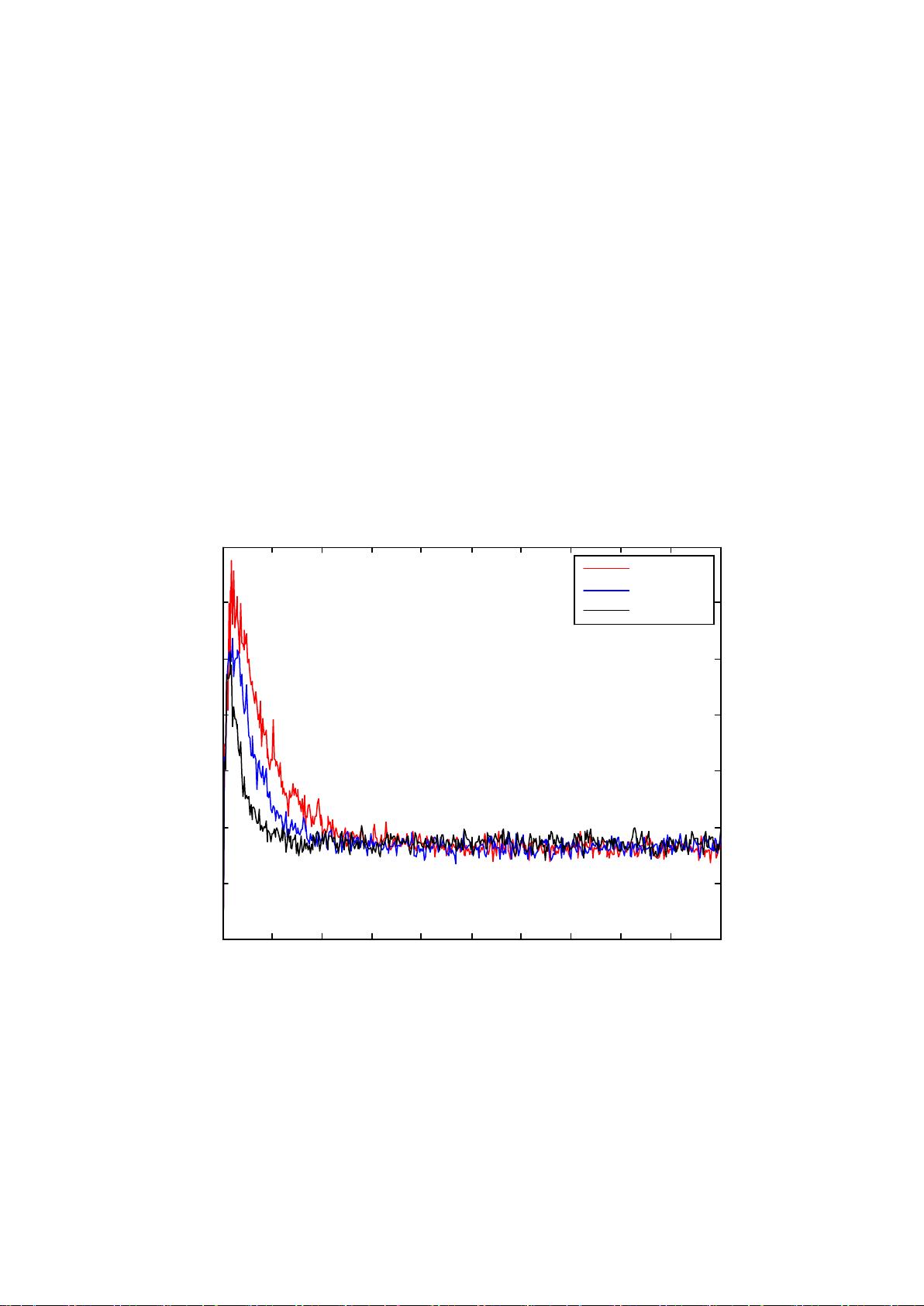**学习曲线**： 图1显示了不同步长下的学习曲线，即随着迭代次数增加，MSE的变化情况。这可以帮助理解不同步长如何影响算法的收敛性能。曲线的斜率反映了MSE下降的速度，可以看出，步长0.015的曲线下降最为平缓，步长0.025次之，而步长0.05的MSE下降最快。 4. **权重更新**： 图2、图3和图4分别展示了每个步长对应的权重（W）随迭代次数的更新路径，以及对应的最终权重向量（WA）。这些图直观地展示了权重如何在迭代过程中变化，以及不同步长下权重更新的快慢和稳定性。 5. **MATLAB实现**： 代码部分使用MATLAB进行实现，调用`lmst`函数执行优化过程，并绘制了结果图。`holdon`命令用于在同一图形窗口中叠加多条曲线，便于比较。`xlabel`、`ylabel`和`title`用于设置图形的标签和标题，而`legend`则给出了不同曲线的标识。 通过这个仿真，我们可以观察到步长选择对信号处理算法性能的影响，这对于优化算法的参数配置和理解其内在工作原理至关重要。在实际应用中，选择合适的步长能有效平衡算法的收敛速度和稳定性，从而提高信号处理的效率和精度。