图论基础:术语、表示与算法详解
需积分: 5 18 浏览量
更新于2024-06-28
收藏 2.89MB PPT 举报
第6章主要探讨了图论在数据结构中的应用,这是计算机科学中一个重要的概念,用于模型化各种现实世界中的关系网络。章节内容涵盖了图的定义和基础术语,包括:
1. **图的定义**:
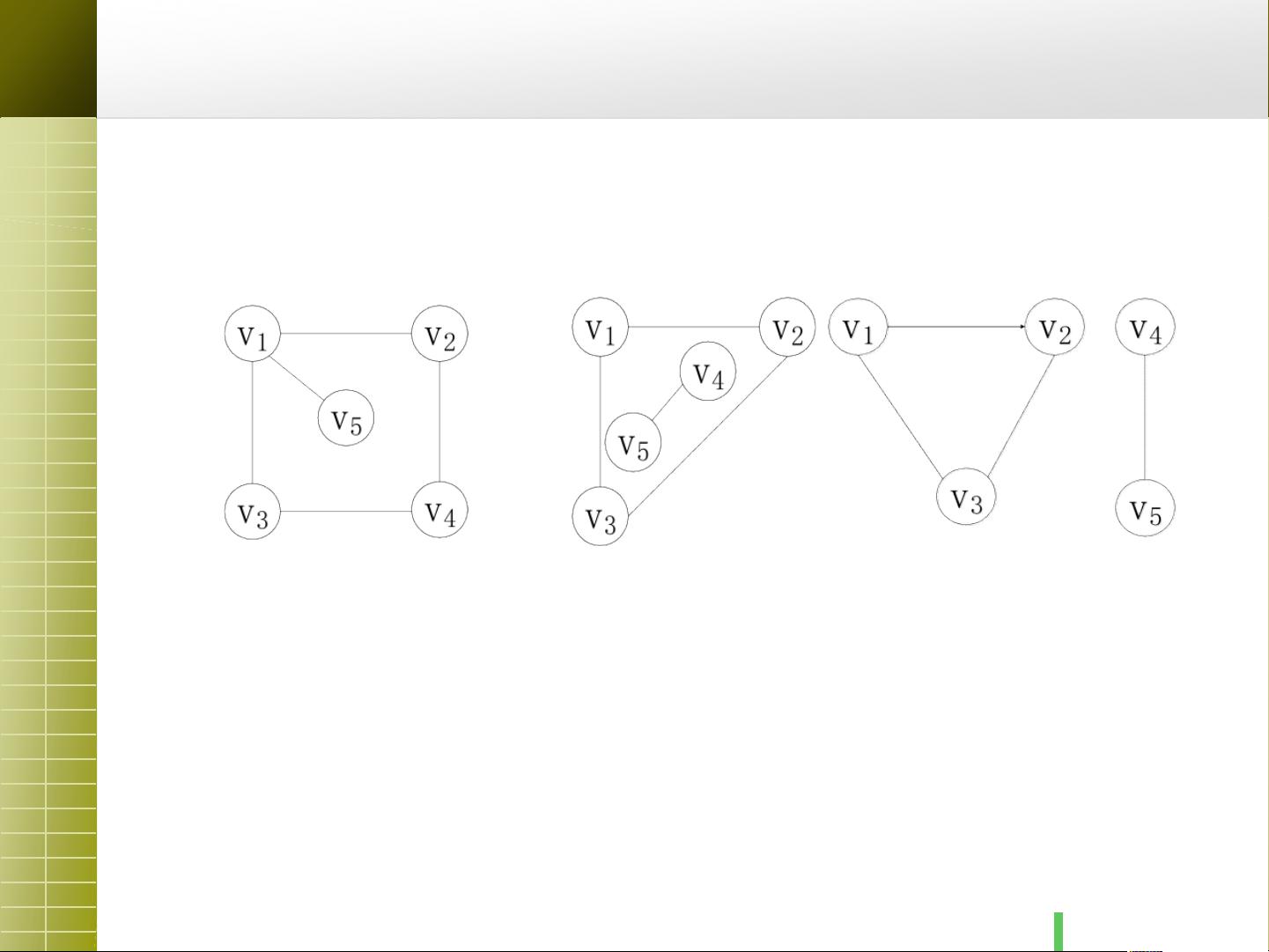
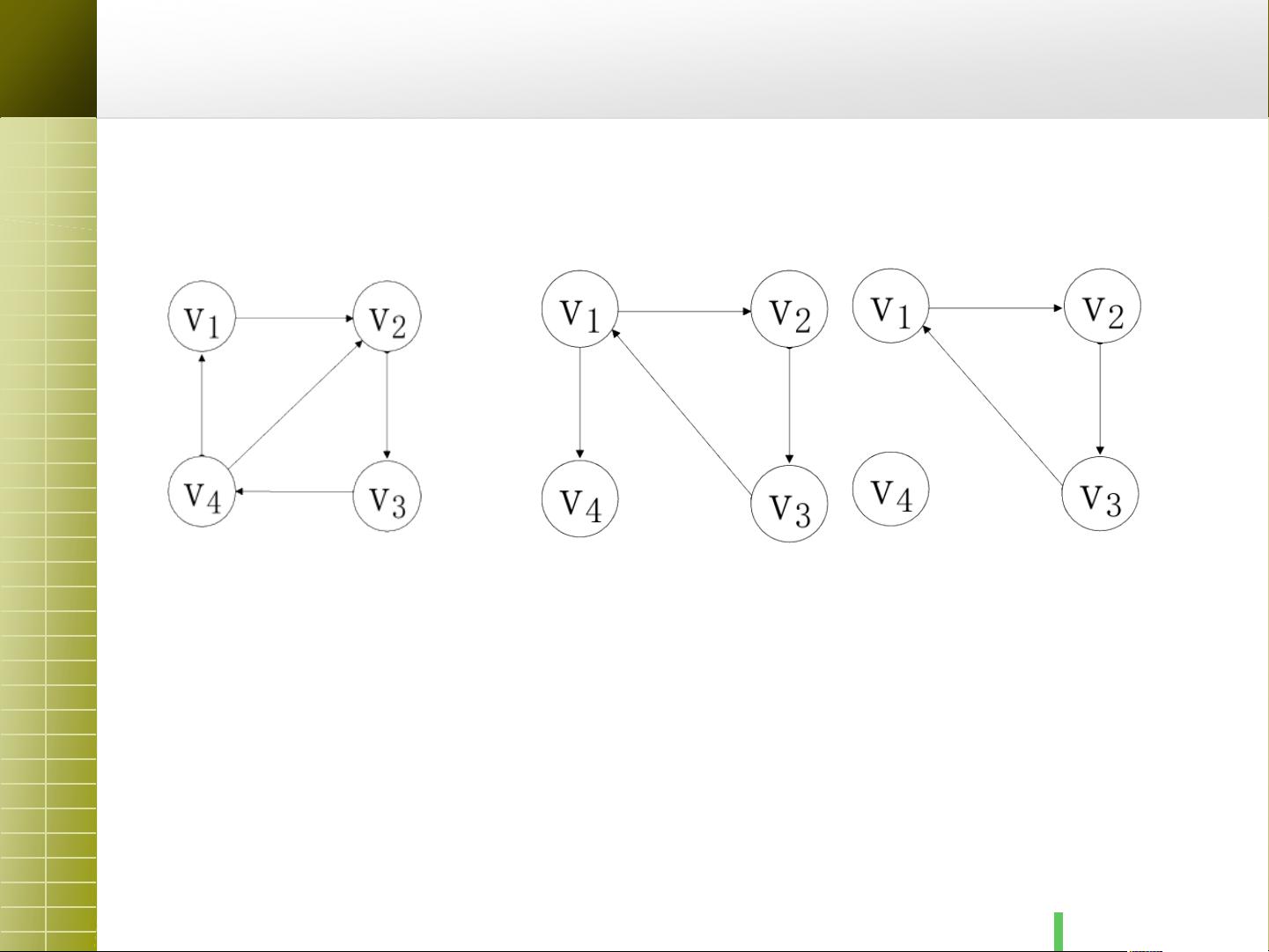
- 图G由两个集合组成:顶点集V(代表数据元素,如城市或网络节点)和边集E(表示顶点之间的连接关系)。对于无向图,边是无方向的,用无序偶对表示;而对于有向图,边有方向,用有序偶对表示。
2. **图的基本术语**:
- **无向边/有向边**:无向边是两点间无方向的连接,如 (vi, vj),而有向边则指定方向,如 <vi, vj>。
- **无向图/有向图**:无向图中的边是双向的,如G1,而有向图如G2中边的方向明确,如<v1, v2>表示从v1到v2的连接。
3. **图的表示方法**:
- **邻接矩阵**:一种以二维数组形式存储图的结构,用0和1表示顶点之间是否存在边。
- **邻接表**:更节省空间的方法,每个顶点有一个链表,包含与其相邻的所有顶点。
4. **图的遍历算法**:
- **深度优先搜索(DFS)**:从某个起点开始,尽可能深地探索分支,直到到达无法继续为止,然后回溯。
- **广度优先搜索(BFS)**:按照距离顺序逐层遍历,先访问离起点最近的节点。
5. **图的应用问题**:
- **最小生成树**:在图中找到一棵包含所有顶点且边权之和最小的树。
- **拓扑排序**:对于有向无环图(AOV网),确定一个线性序列,使得对于每条有向边(u, v),节点u总是在序列中出现在节点v之前。
- **关键路径**:在AOE网中,最长的任务完成时间路径,影响整个项目的最早完成时间。
- **最短路径**:寻找两个顶点之间的最短路径,如Dijkstra算法或Floyd-Warshall算法。
**学习重点**在于理解图的存储方式,掌握图的遍历算法,以及如何解决实际问题,如找到最小生成树和最短路径。这些概念不仅在理论研究中有重要意义,也在网络编程、算法设计、社交网络分析等领域有着广泛的应用。
2021-11-05 上传
係恆
- 粉丝: 0
- 资源: 8
最新资源
- 正整数数组验证库:确保值符合正整数规则
- 系统移植工具集:镜像、工具链及其他必备软件包
- 掌握JavaScript加密技术:客户端加密核心要点
- AWS环境下Java应用的构建与优化指南
- Grav插件动态调整上传图像大小提高性能
- InversifyJS示例应用:演示OOP与依赖注入
- Laravel与Workerman构建PHP WebSocket即时通讯解决方案
- 前端开发利器:SPRjs快速粘合JavaScript文件脚本
- Windows平台RNNoise演示及编译方法说明
- GitHub Action实现站点自动化部署到网格环境
- Delphi实现磁盘容量检测与柱状图展示
- 亲测可用的简易微信抽奖小程序源码分享
- 如何利用JD抢单助手提升秒杀成功率
- 快速部署WordPress:使用Docker和generator-docker-wordpress
- 探索多功能计算器:日志记录与数据转换能力
- WearableSensing: 使用Java连接Zephyr Bioharness数据到服务器