决策树实战：熵与划分

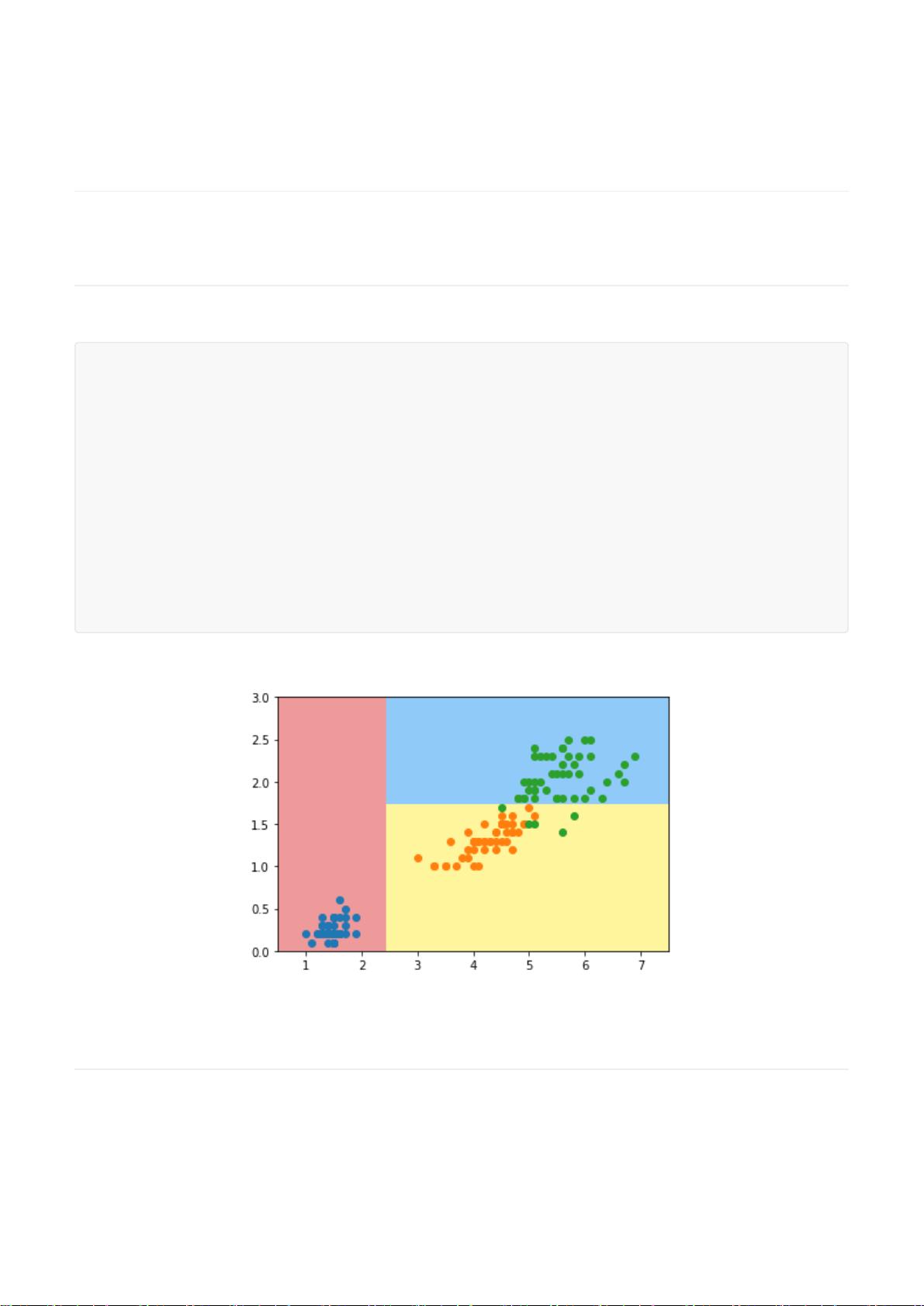
"决策树实战1" 在这篇关于决策树实战的文章中，我们将深入理解决策树这一机器学习模型，并通过实际代码示例进行演示。决策树是一种广泛应用的分类算法，它以树状结构来表示可能的决定过程，其中内部节点表示特征测试，分支代表测试结果，而叶节点则给出类别决策。 在"01WhatisDecisionTree"部分，作者展示了如何使用Python的scikit-learn库创建一个简单的决策树模型。`DecisionTreeClassifier`是scikit-learn提供的决策树分类器，可以通过调用其`fit`方法训练模型，用`predict`方法进行预测。为了更好地理解决策树的工作原理，可以运行对应的notebook文件，查看决策树如何根据数据划分样本。 "02Entropy"章节探讨了决策树划分数据的基础——熵。熵是信息论中的一个概念，用来衡量随机变量的不确定性。在决策树中，熵用于度量数据集的纯度，即数据集中各类别的均匀程度。如果熵值高，表示数据集的类别分布不均匀，不确定性大；反之，熵值低，表示数据集的类别分布较为集中。在构建决策树时，我们希望选择能最大程度降低熵（增加数据纯度）的特征进行划分。决策树通常采用基尼不纯度或熵作为划分标准，这里使用的是熵。 熵的数学公式定义为： \[ H(Y) = -\sum_{i=1}^{n} p_i \log_2 p_i \] 其中，\( H(Y) \) 表示熵，\( n \) 是类别数量，\( p_i \) 是第 \( i \) 类别的概率。熵的取值范围在0到1之间，当所有类别概率相等时，熵最大，等于1；当只有一种类别时，熵最小，等于0。 "03EntropySplitSimulation"部分介绍了如何利用熵来寻找最佳的特征划分。通过计算不同特征和特征值划分后子集的熵，我们可以找到使熵减少最多的划分方式，这种方法类似于ID3算法。ID3算法基于信息增益（信息熵的减少）选择最优特征进行划分，以达到数据的最大纯度。 在实际的代码段中，`entropy`函数计算给定类别列表的熵，而`try_split`函数尝试所有特征和特征值的组合，寻找熵减少最大的划分。这些函数的实现可以帮助我们理解决策树在构建过程中如何做出决策。 这篇实战文章提供了决策树的基本概念和Python实现，帮助读者从理论和实践两方面掌握决策树的工作原理和应用。通过运行提供的notebook文件，读者可以动手操作，加深对决策树的理解。