数据结构：平均时间复杂度与分摊时间复杂度解析

本资源主要讨论了数据结构中的向量，并着重分析了向量操作的时间复杂度，包括平均时间复杂度和分摊时间复杂度。同时，提到了这两个概念的区别和应用场景，以及如何通过分摊分析来更准确地评估算法性能。另外，还涉及了在数组复制操作中，如何处理目标数组与源数组可能存在的空间重叠问题。 在数据结构中，向量是一种基础且常用的数据结构，它以线性方式存储元素，支持动态扩展和收缩。本章节的讨论聚焦于向量操作的时间复杂度分析，特别是算法分析的两个重要概念：平均时间复杂度和分摊时间复杂度。 平均时间复杂度是根据各种输入实例可能出现的概率分布来计算的加权平均运行时间。它在评估算法性能时，假设输入实例遵循一定的概率模型。例如，对于快速排序，如果假定待排序元素是独立且均匀随机分布的，可以计算其平均时间复杂度。 分摊时间复杂度则更注重算法的全局行为，考虑连续多次操作的整体时间，并将这个时间平摊到每一步操作上。这种方法适用于那些操作之间有因果关系的算法，如伸展树的插入和删除操作。分摊分析可以揭示单次操作的实际成本，即使这些操作在实际应用中并不独立。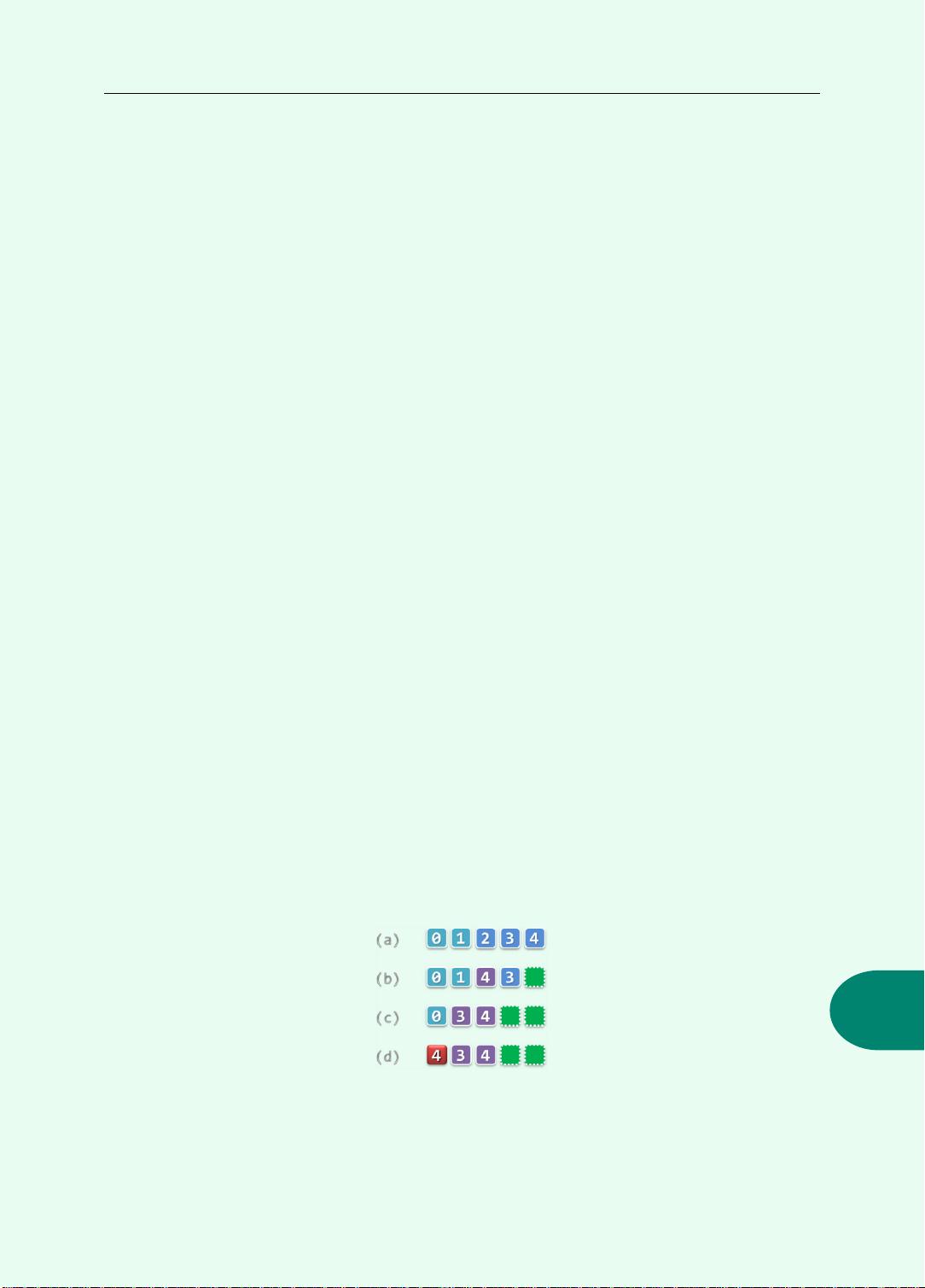 以可扩充向量为例，如果简单地用平均分析方法，可能会因不准确的概率分布假设（如扩容与不扩容事件概率相等）而得出错误的性能评估。而通过分摊分析，我们可以看到采用容量加倍策略的向量在实际运行中，随着容量增加，扩容事件的概率会迅速降低，从而更准确地理解其性能。 在实际编程中，数组复制操作必须确保目标数组与源数组的物理独立性，以避免数据污染。如果无法保证这种独立性，算法需要进行调整，例如使用临时数组或者采取其他避免空间重叠的策略。教材中的`copyFrom()`算法即是一个例子，如果目标数组不是独立分配的，那么在复制过程中可能需要额外的检查和处理，以确保数据的正确性。 本章节深入探讨了向量操作的复杂度分析，强调了平均时间复杂度和分摊时间复杂度在算法评估中的差异和应用，并通过实例讲解了如何处理可能的空间重叠问题，这些都是理解和优化数据结构与算法设计的关键点。