提升常规网络t/k诊断性算法与复杂度分析

44 浏览量更新于2024-08-26 收藏 818KB PDF 举报

本文主要探讨了"常规网络的t=k可诊断性"这一主题，该研究聚焦于多处理器系统中的诊断策略。t=k诊断策略是一种旨在增强系统自我诊断能力的方法，其核心思想是在概率模型（PMC模型）下，允许最多有k个非故障处理器被误判为故障，同时仍能检测到总共不超过k个实际故障处理器。这可以看作是精确和悲观诊断策略的扩展，特别适用于具有高可靠性的网络系统。在常规网络（如环形、星形或网格网络）中，当k=1时，目前尚未发现有效的t=k诊断算法。然而，本研究填补了这一空白，作者Lieming Lin、Li Xu（IEEE成员）、Shuming Zhou和Sun-Yuan Hsieh（IEEE高级成员）首先提出了针对某些特定m-正规网络的t=k诊断(k>1)算法。这些m-正规网络满足一定的条件，使得可以建立一种被称为t=k-G-DIAG的诊断方法，用于判断网络是否具备t=k可诊断性。这个算法的关键贡献在于其高效性。当网络的处理器数量N大于2m时，其复杂度为O(N log N)，而当N小于2m时，复杂度降为O(Nm)。这样的复杂度表明，算法能够在合理的时间内处理大规模网络，提高了诊断的实时性和实用性。此外，文章还全面介绍了该算法的工作原理、适用条件以及如何确保其正确执行。通过这种方法，研究人员希望能够提高常规网络在面临故障时的快速定位和恢复能力，从而提升系统的整体健壮性和可靠性。这对于设计和维护现代通信网络、分布式系统和其他关键基础设施具有重要意义。这篇研究论文不仅为常规网络的t=k可诊断性提供了一种新的理论框架，还为实际应用中的故障检测与隔离提供了实用工具。

empirical analysis of some known networks. Section 5 gives

some concluding remarks.

2PRELIMINARIES

In this section, we ﬁrst propose some terms and notations

about the combinatorial graph theory. These terms and

notations could play a basis role, which are necessary. Sec-

ond, we give the deﬁnition of t=k-diagnosis and t=k-diag-

nosability under the PMC model. These deﬁnitions will

welly help us to complete our goals.

2.1 Terms and Notations

In a parallel computing system, processors are connected

based on a speciﬁc interconnection network. An intercon-

nection network is conveniently represented by an undi-

rected graph. Throughout this paper, we use the terms

vertex, edge and graph to replace the terms processor, link

and network, respectively. For other fundamental graph-

theoretic and interconnection network terminologies not

deﬁned here we follow [38].

Let G be a simple undirected graph. We use V ðGÞ and

EðGÞ to denote the sets of vertices and edges of G, respec-

tively. Here, a vertex u 2 V ðGÞ represents a processor and an

edge uv 2 E ðGÞ represents a link between vertices u and v.

Also, jV ðGÞj and jEðGÞj denote the numbers of vertices and

edges of G, respectively. For any two graphs G

ðV ðG

Þ;EðG

ÞÞ and G

¼ðV ðG

Þ;EðG

ÞÞ, we denote G

[ G

(resp., G

\ G

) as a graph with vertex-set V ðG

Þ[ V ðG

(resp., V ðG

Þ\V ðG

Þ)andedge-setEðG

Þ[EðG

Þ (resp.,

EðG

Þ\EðG

Þ). For a vertex v 2 V ðGÞ, N

ðvÞ denotes the set

of vertices adjacent to v,calledtheneighborhood of v. The cardi-

nality of jN

ðvÞj is called the degree of v,denotedbyd

ðvÞ.If

X, Z  V ðGÞ and v 2 V ðGÞ, the neighborhood of v in X is

denoted by N

ðvÞ :¼ N

ðvÞ\X,andN

ðZÞ :¼

u2Z

ðuÞ.

The subscript “G” can be removed from the notation if there is

no ambiguity. For any graph G ¼ðV ðGÞ;EðGÞÞ with one sub-

set V

 V ðGÞ,theprivate neighbors of one vertex v 2 V

denoted by PNðvÞ, are those neighbors of v which are not

shared by other vertices in V

and are not themselves in V

i.e., PNðvÞ¼NðvÞðNðV

fvgÞ [ V

Þ.

The subgraph of G induced by S,denotedbyG½S,isthe

graph with the vertex-set S and the edge-set fuv j

uv 2 EðGÞ;u;v2 Sg. For any two subsets A and B of V ðGÞ,

the notation A  B denotes as a set obtained by removing all

vertices in B from A. For any subset F  V ,thenotation

G  F denotes as a graph obtained by removing all vertices in

F from G and deleting those edges with at least one end-

vertex in F, simultaneously, i.e., V ðG  FÞ¼V  F , EðG 

F Þ¼fuv 2 E j u; v 2 V  Fg. The maximal connected sub-

graphs of G  F are called components.LetmcðGÞ

denote the

number of vertices in the largest component of G. S is called a

vertex-cut of a graph G if and only if G  S is disconnected or a

single-vertex. The connectivity of a graph G, denoted kðGÞ,is

deﬁned as the minimum cardinality of a vertex cut of G.A

k-connected graph is a graph G with kðGÞk.Ak-regular

graph is maximally connected if it is k-connected.

2.2 t=k-Diagnosis under the PMC Model

We introduce some notations ﬁrst. Consider a multiproces-

sor system G ¼ðV ðGÞ;EðGÞÞ. The fault-set of G is the set of

all faulty vertices of G. This paper adopts the PMC model.

Under the classical PMC model [30], any two adjacent verti-

ces are capable of performing tests on each other. For any

two adjacent vertices u; v 2 V ðGÞ, the ordered pair ðu; vÞ rep-

resents a test that the vertex u tests the vertex v. In this case, u

is called the tester and v is called the tested vertex. Thus, the

self-testing capability of G can be described by its bi-direc-

tionally oriented digraph DðGÞ¼ðV ðGÞ;AðGÞÞ. A test

assignment on G can be a sub-digraph of DðGÞ. To make the

full use of the self-diagnosing capability of G, this paper will

take DðGÞ itself as the test assignment, i.e., all nodes test all

neighboring vertices. Consider two adjacent vertices, u and

v, of a graph G. The outcome of the test conducted by u on v,

denoted by sðu; vÞ, assumes the value 0 or 1 depending on

whether u evaluates v as “fault-free” or as “faulty”, respec-

tively. We also use sðu; vÞ$

sðv; uÞ to denote the syndrome

that u and v test each other. The whole collection of the test

outcomes, denoted by s, is referred to as a syndrome on G.

The PMC model assumes that a fault-free vertex can cor-

rectly evaluate all of its neighbors, whereas the outcome of a

test conducted by a faulty vertex is completely unreliable.

The basic idea behind the t=k-diagnosis is to enhance the

self-diagnosing capability of multiprocessor at the expense

of lower diagnosis demand [15], [32], [33]. Speciﬁcally, the

t=k-diagnosable deﬁnition of a system is given as follows.

Deﬁnition 1. [33] A multiprocessor system G of n units is

t=k-diagnosable if, given any test syndrome produced by the

system under the presence of a faulty set F , all the faulty pro-

cessors can be isolated to within a set of processors F

, out of

which at most k processors can possibly be fault-free

ðincorrectly diagnosedÞ, jF

jjF jþk, provided the number

of faulty processors does not exceed t.

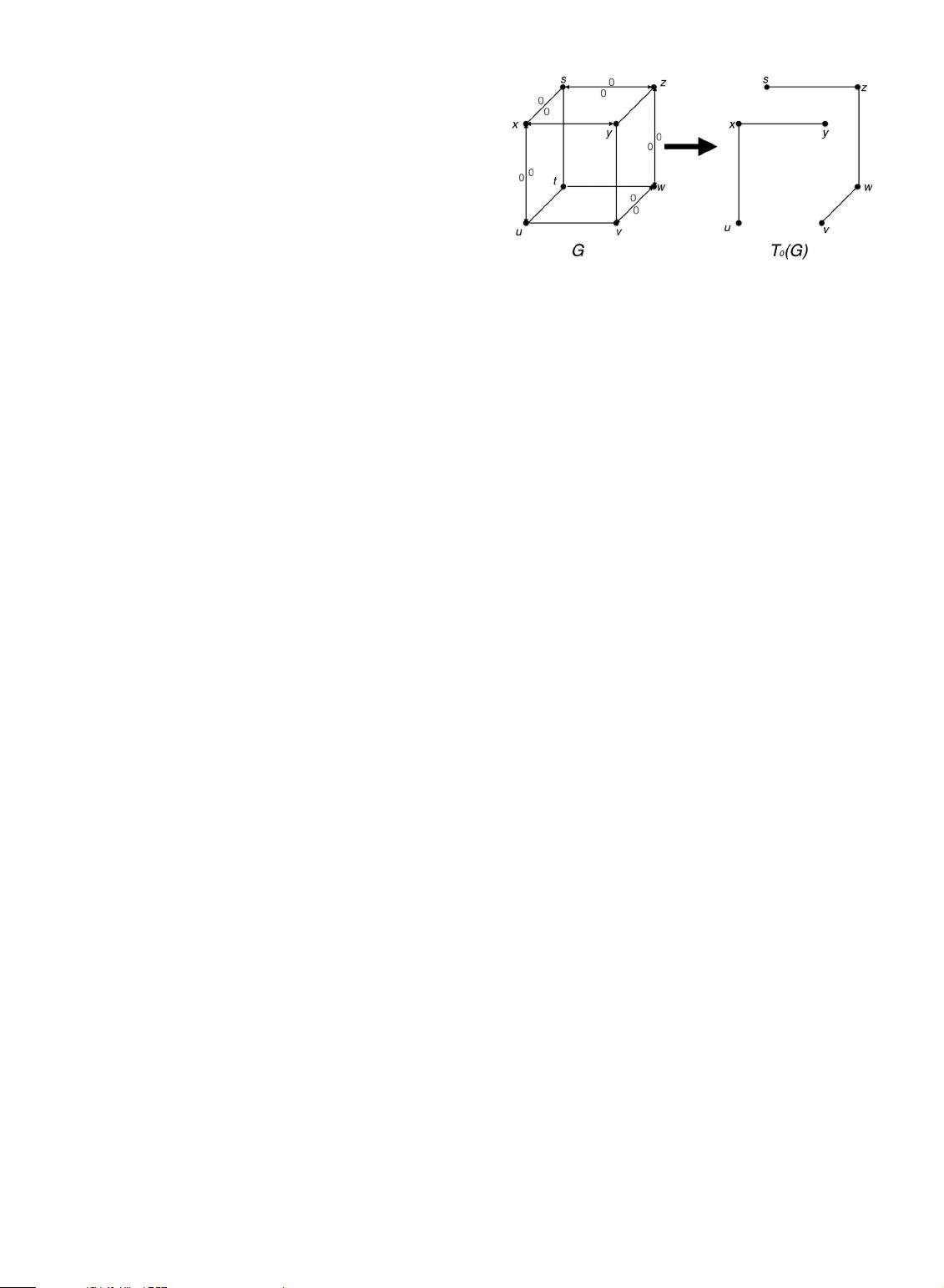
Next, we introduce the 0-test subgraph, say T

ðGÞ,ofG,

which plays a very important role in our t=k-diagnosis

algorithm.

Deﬁnition 2. [42] Given a graph G ¼ðV ðGÞ;EðGÞÞ and a syn-

drome s on G produced by a faulty set. The 0-test subgraph of

G,denotedT

ðGÞ, is a subgraph of G deﬁned by V ðT

ðGÞÞ  V

and EðT

ðGÞÞ ¼ fuv 2 E j sðu; vÞ¼sðv; uÞ¼0g (see Fig. 1).

3AGENERAL ALGORITHM OF t=k-DIAGNOSIS

ANALYSIS FOR SOME REGULAR NETWORKS

In this section, we will propose a general t=k-diagnosability

analysis for some regular networks to establish the t=k -diag-

nosability. First, we give some available results when the net-

work G satisﬁes some conditions. When a regular network G

Fig. 1. The illustration of the 0-test subgraph T

ðGÞ.

LIN ET AL.: THE t=k-DIAGNOSABILITY FOR REGULAR NETWORKS 3159

剩余13页未读，继续阅读

weixin_38693753

粉丝: 9
资源: 993

提升常规网络t/k诊断性算法与复杂度分析

DeviceNet 网络故障诊断指导

华为ONT维修使能(国内版本)

常规仪表基础知识.pdf

康佳T2528H型彩电上拉电阻开路导致CPU死机的检修.pdf

PID控制器失效检测与故障诊断方法研究

【NodeManager日志分析】：解读NodeManager日志与故障诊断的全面教程

【算法故障诊断与解决】：快速定位与修复排序过程中的错误

Ubuntu服务器版高级配置技巧：网络、存储与虚拟化优化方法

RNN注意力机制：提升性能的突破性策略

httpx的SSL_TLS配置：提升安全性的最佳实践

最新资源