MATLAB实现傅立叶变换详解

"该PDF文档主要介绍了傅立叶变换在MATLAB中的实现方法，包括了傅立叶分析的基础知识，如各种常用函数的定义与性质，以及傅立叶变换的相关概念和性质。文档详细讲解了阶跃函数、符号函数、矩形函数等函数的定义和MATLAB实现，同时提到了卷积的概念及其在MATLAB中的应用。此外，还讨论了傅立叶变换的存在条件、周期函数的变换、数值实现等内容，并给出了几种常见图形的傅里叶变换实例。" 傅立叶变换是一种重要的数学工具，广泛应用于信号处理、图像分析、工程计算等多个领域。在MATLAB中，傅立叶变换的实现通常利用内置函数`fft`来进行。这个文档详细介绍了傅立叶变换的理论基础和实际应用。 首先，文档列举了几种常用的函数，如阶跃函数（Step Function），在MATLAB中可以通过`step(x)`函数来实现，它在x小于0时返回0，等于0时返回1/2，大于0时返回1。符号函数（Signum Function）`sgn(x)`则返回x的符号，当x大于0时返回1，等于0时返回0，小于0时返回-1。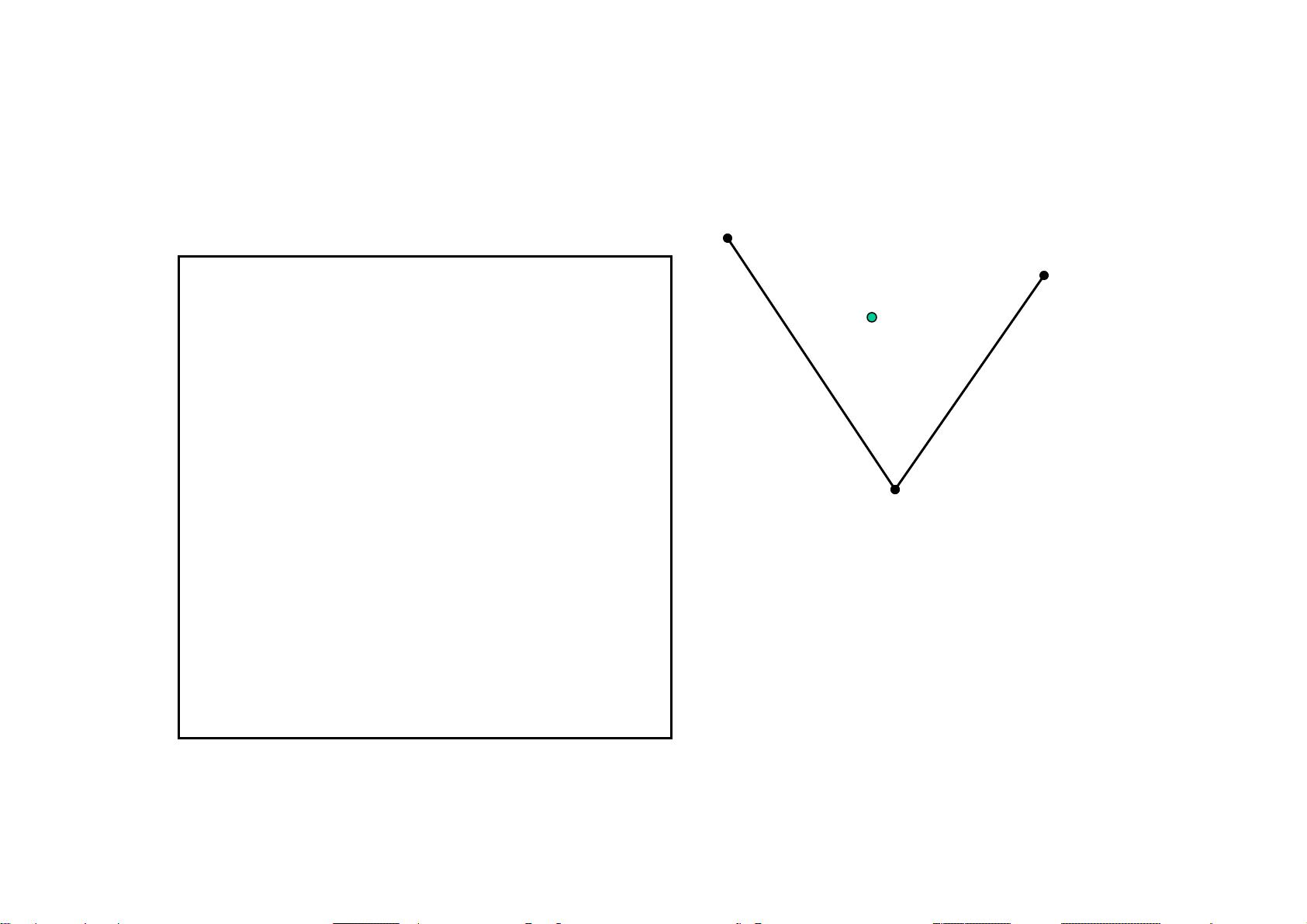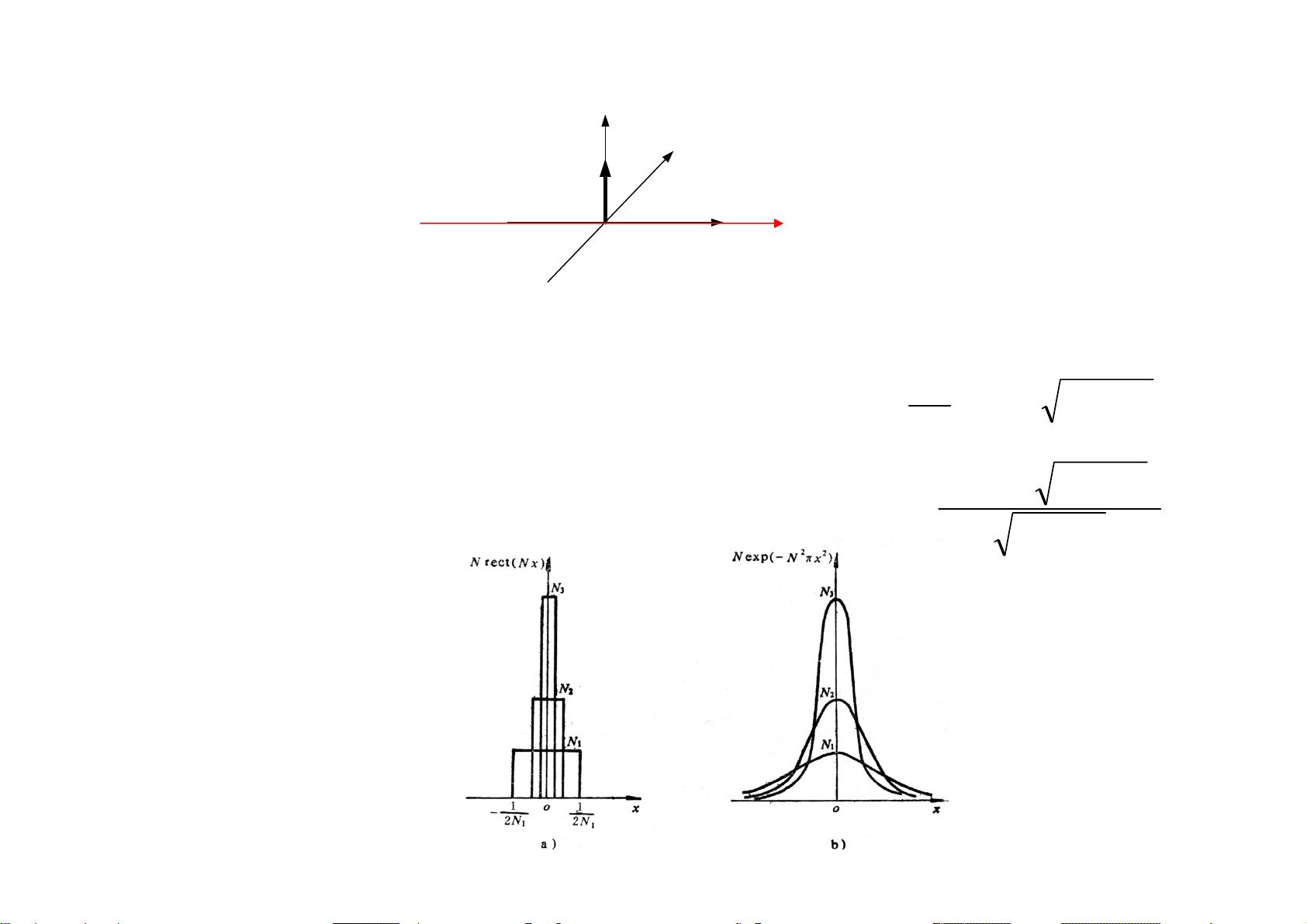 接着，文档提到了矩形函数（Rectangular Function），也称为单位脉冲函数，它在一定区间内为1，其余地方为0。在MATLAB中，虽然没有直接的内置函数表示矩形函数，但可以通过逻辑运算或自定义函数实现。 卷积是傅立叶变换的一个关键概念，它在信号处理中用于描述两个函数的相互作用。卷积的MATLAB实现可以使用`conv`函数。卷积在物理意义上代表了一个系统对输入信号的响应，具有一定的线性特性。 傅立叶变换定义了一个函数在频域的表示，它是原函数在时域的傅立叶积分。在MATLAB中，`fft`函数用于计算离散傅立叶变换（DFT），而`ifft`则用于计算反变换。对于不同类型的函数，例如实数、虚数、奇函数、偶函数，傅立叶变换有不同的性质。文档还讨论了可分离函数的傅立叶变换以及周期函数的傅里叶级数。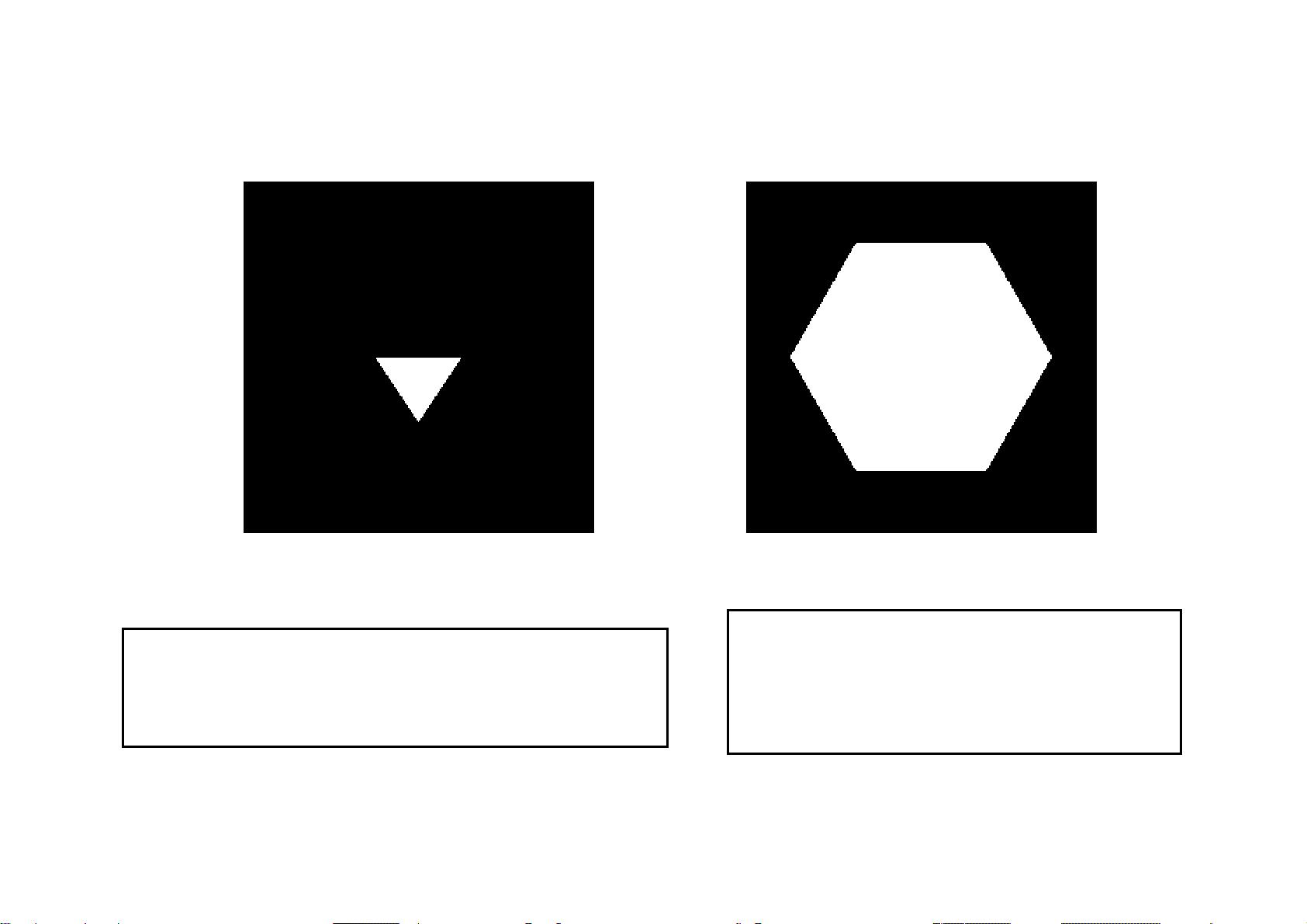 最后，文档介绍了如何通过MATLAB进行傅立叶变换的数值实现，这对于理解和应用傅立叶变换在实际问题中至关重要。通过学习这些内容，读者可以更好地掌握傅立叶变换的理论知识，并在MATLAB环境中进行实际操作，解决相关问题。