"2021春图的深度优先搜索与广度优先搜索算法"

本文主要讨论了图相关的算法和数据结构，其中第四章主要介绍了图的路径问题和图的遍历。图的遍历包括了深度优先搜索DFS和广度优先搜索BFS两种方法。在深度优先搜索中，首先访问起点，然后依次访问与该起点相关联的每一个顶点，并以该关联顶点为新的起点，继续深度优先遍历。若图中还有未被访问的顶点，则换一个起点，继续深度优先遍历，直到所有的顶点都被访问。而在广度优先搜索中，则是先访问起点的所有邻接顶点，再访问这些顶点的相邻顶点，依此类推，直到所有顶点都被访问。 此外，对于图的遍历，还需注意确定遍历起点、保证非连通图的每一顶点都能被访问到、避免顶点的重复访问等问题。图的遍历是图算法中的基础部分，是解决许多图相关问题的关键步骤。在实际应用中，图的遍历可以用来寻找路径、查找连通分支、计算连通分支的数量等。 在进行图的遍历时，深度优先搜索和广度优先搜索各有其特点和适用场景。深度优先搜索适用于查找连通分支、寻找路径等问题，而广度优先搜索适用于计算连通分支的数量、检测环路、计算最短路径等问题。同时，这两种搜索算法也可以相互转化，即可以用深度优先搜索来找到所有可能的路径，再用广度优先搜索来求解最优路径。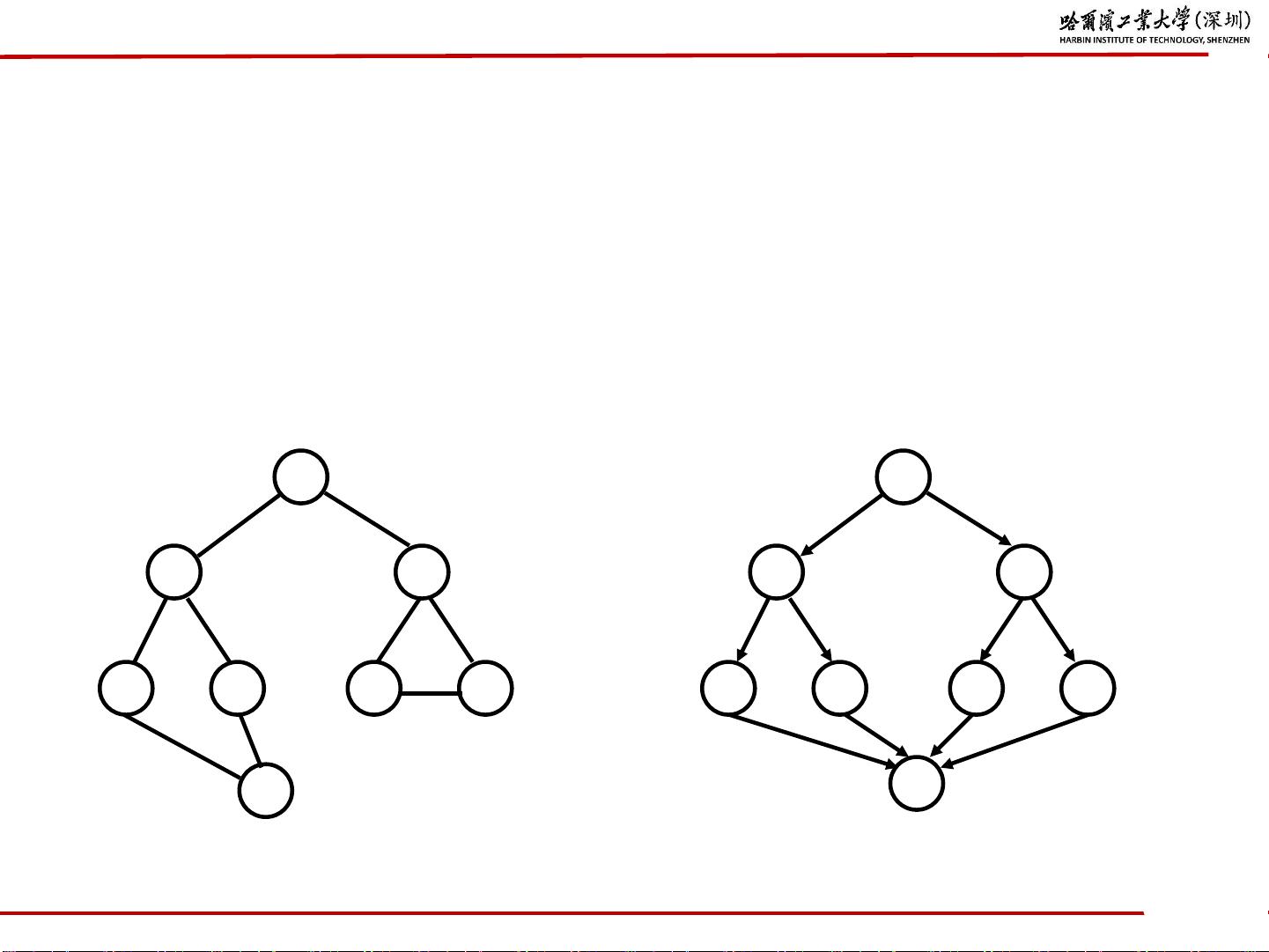 在图的搜索算法中，还需要考虑图的类型，包括有向图和无向图。有向图中的边是有方向的，而无向图中的边是没有方向的。对于有向图和无向图的搜索算法，也有着一些差异。比如在无向图中，深度优先搜索和广度优先搜索的应用更为广泛，而在有向图中，可以通过拓扑排序解决一些特殊的问题。 总的来说，图的搜索算法是图算法中的重要内容，对于解决各种图相关问题具有重要的作用。通过深度优先搜索和广度优先搜索，可以更好地理解图的结构和特点，解决实际应用中的各种问题。对于计算机科学与技术学院的学生来说，深入理解和掌握图的搜索算法对于提高算法设计和分析的能力，具有重要的意义。因此，建议学生在学习数据结构与算法的过程中，加强对图相关知识的学习和掌握，提高对图搜索算法的理解和应用能力。