优化Hilbert八叉树邻近计算：算法与效率提升

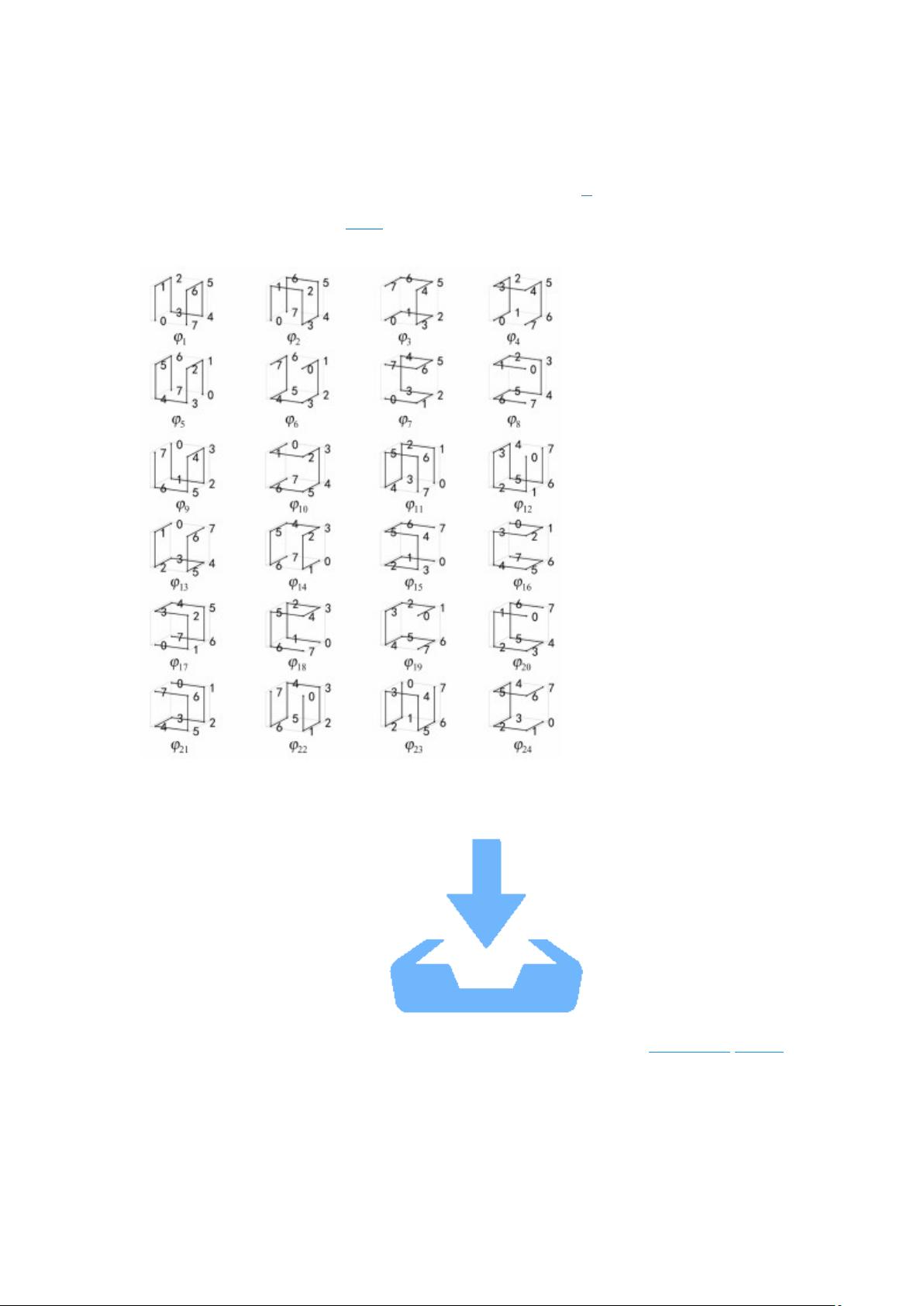
"该文档涉及的是面向Hilbert八叉树的邻近格元计算算法，主要探讨了Hilbert曲线在三维空间数据组织和邻域查找中的应用。Hilbert八叉树因其节省存储空间和包含层次信息的特性而被广泛采用。其中，Hilbert码的聚簇效果使得空间数据的分布更为紧凑。邻近格元的Hilbert码计算是高效八叉树邻域计算的核心，通常通过Morton码转换来实现，但这种方法存在计算复杂度高的问题。" 本文档详细介绍了三维Hilbert曲线的概念，它将三维空间分割成规则的格元，并通过不遗漏、不交叉的路径遍历所有格元。线性八叉树的叶节点Hilbert码代表了节点在Hilbert曲线上的顺序，这对于空间操作如聚类、索引和查询至关重要。八叉树的邻域计算通常包括两步骤：计算中心格元的邻近Hilbert码，然后在八叉树中查找对应叶节点。 在邻近格元Hilbert码的计算中，常见的方法是利用Morton码（Z-Order码）与Hilbert码之间的转换。首先将Hilbert码转化为Morton码，再通过位操作找出邻近的Morton码，最后转换回Hilbert码。然而，这种转换方法存在计算复杂度较高的问题，特别是在处理高层数的格元时，效率会显著下降。 为了解决这一问题，文献提出了无需转换到其他编码形式，直接利用Hilbert曲线自身特性来计算邻近格元Hilbert码的新方法。这种方法可能通过记录中心格元在各级别的相对位置和Hilbert曲线的性质，提高了计算效率，降低了计算时间复杂度，尤其对于大规模、高分辨率的空间数据处理，能显著提升性能。 面向Hilbert八叉树的邻近格元计算算法是空间数据管理和查询的关键技术，优化这种算法对于提高空间索引和查询的速度具有重要意义。文献中提到的直接使用Hilbert曲线性质的方法，旨在克服现有转换方法的效率瓶颈，为高效的空间数据操作提供新的解决方案。