超低功耗13位6.4 MS/s SAR ADC：背景不匹配与偏置校准技术

需积分: 23 53 浏览量更新于2024-09-10 收藏 3.85MB PDF 举报

"A 46 μW 13 b 6.4 MS/s SAR ADC With Background Mismatch and Offset Calibration" 这篇论文介绍了一种低功耗、高分辨率的模数转换器（ADC），具体来说，是一种采用逐次逼近寄存器（SAR）架构的ADC。该ADC具有出色的性能参数，其电源消耗仅为46微瓦（μW），能够实现13位的分辨率，并以6.4兆样本每秒（MS/s）的速度进行采样。这些特性使得它非常适合于能源受限的应用，例如无线传感器网络、物联网设备以及便携式电子设备。在ADC设计中，失调和不匹配问题通常会影响转换精度。该论文提出的SAR ADC引入了背景校准技术来解决这些问题。背景校准是在不影响正常采样操作的同时，对电路中的失调电压和不匹配误差进行动态补偿，从而提高了ADC的线性度和整体性能。这种方法的关键在于能够在运行时自动调整，无需额外的外部控制信号或复杂的校准序列，降低了系统的复杂性和功耗。论文中提到的几位作者，如M. Ding、Yao-Hong Liu、Benjamin Busze和K. Philips，他们在Imec Netherlands和Holst Centre等研究机构工作，这些机构在微电子和射频技术领域有着深厚的积累。他们的研究项目包括可植入RF收发器设计和生命体征检测雷达，这进一步证明了这款SAR ADC对于生物医学和健康监测应用的潜力。此外，文章中提到的DOI（数字对象唯一标识符）10.1109/JSSC.2016.2609849表明，该研究成果已发表在《IEEE Journal of Solid-State Circuits》上，这是一个在集成电路领域非常权威的学术期刊。这意味着论文经过了同行评审，其科学性和技术价值得到了业界的认可。这个46 μW 13位6.4 MS/s的SAR ADC展示了高效率与高精度的结合，其背景失调和不匹配校准技术是提高ADC性能的关键创新。这一技术在低功耗系统和高分辨率传感器应用中具有广泛的应用前景。

This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination.

2 IEEE JOURNAL OF SOLID-STATE CIRCUITS

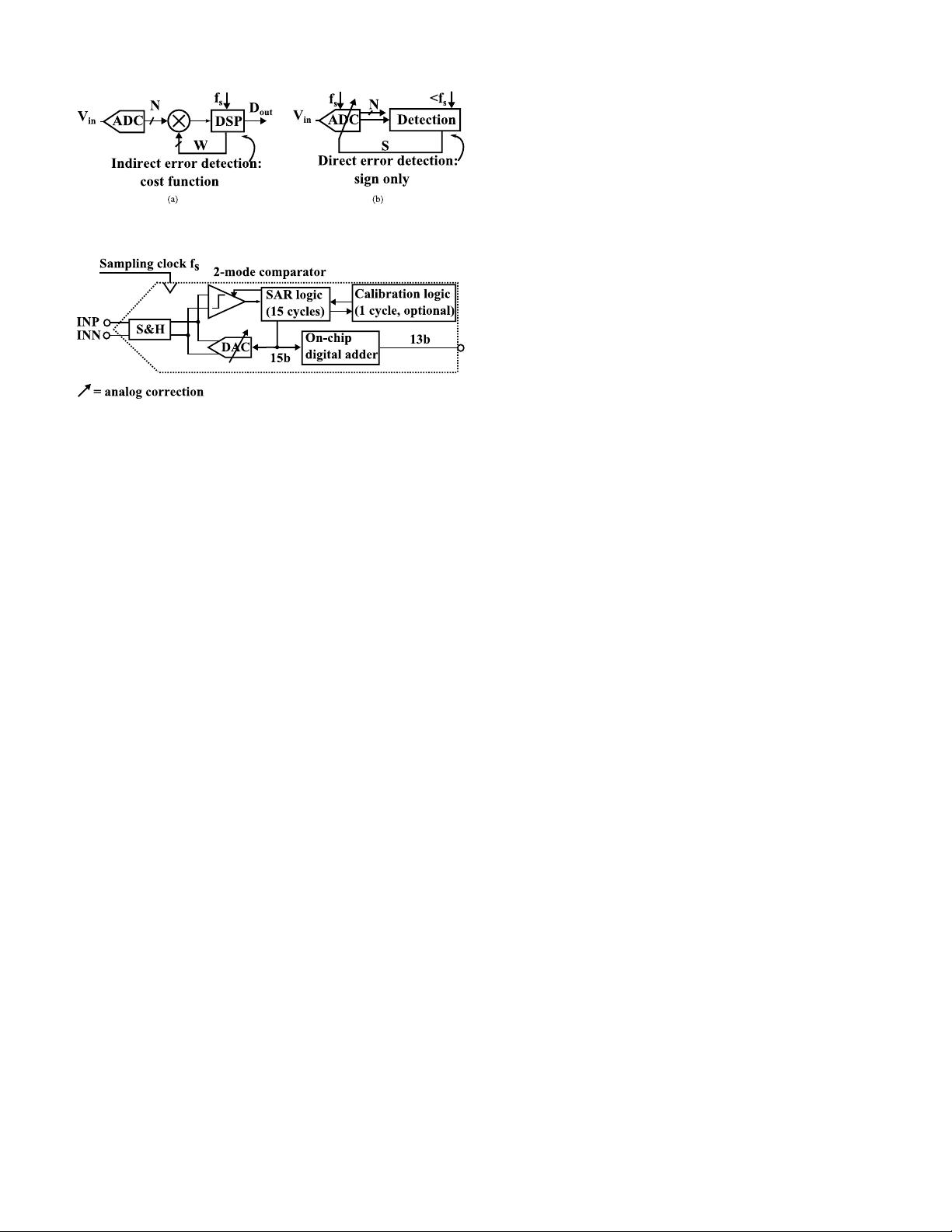
Fig. 1. (a) Block diagram of the prior arts’ calibration method and

(b) proposed calibration method for a N bit ADC.

Fig. 2. Block diagram of a 13 b SAR ADC.

In prior art, without knowing any information of the error,

often the circuit errors are corrected indirectly in a digital

fashion [2], [3], [10] via postprocessing. Fig. 1(a) shows the

block diagram of the calibration method in [2], [3], and [10].

Based on the ADC output data, a DSP engine can deﬁne a

cost function, which reﬂects the error. Through an adaptive

algorithm, e.g., LMS, the value of the cost function will

be tuned toward zero once the coefﬁcients W are correctly

trained. To guarantee the precision of the coefﬁcient training,

redundancy is usually introduced in the DSP engine. On the

other hand, a direct error detection and correction scheme is

proposed as shown in Fig. 1(b). The sign of error can be

detected as shown later. Thanks to the feedback loop and the

analog correction circuit, it is very convenient to stepwise

tune the error toward zero based on its sign. In this way,

only the sign needs to be processed compared with the whole

ADC output in Fig. 1(a). Besides, power-hungry operations

[e.g., multiplying in Fig. 1(a)] are avoided and only much

simpler calculations (e.g., accumulation) are needed. Further-

more, instead of a blind algorithm requiring many iterations,

the sign of the individual errors can be directly detected to

compensate these errors, reducing the convergence time and

required energy. Moreover, the actual correction is in analog

domain instead of digital signal processing as shown later,

consuming far less power. Overall, the proposed calibration

method has very little overhead in circuit complexity, area,

speed, and power.

A. ADC Architecture

Fig. 2 shows the architecture of the 13 b SAR ADC.

In each SAR conversion, ﬁrst, the S&H samples the differ-

ential analog input voltage on the capacitor arrays inside the

DAC. Using the comparator and the logic, the DAC output

will approximate the sampled input voltage in several com-

parisons through a successive-approximation algorithm using

a monotonic switching scheme [16]. In this design, a total of

15 cycles is used to perform a 13 b conversion, where two of

them are redundant cycles to overcome various errors during

the conversion (e.g., DAC settling and noise), similar to [14].

The 13 b output is calculated from the 15 b raw code by an

on-chip digital adder. A two-mode comparator is introduced

to save power while still maintaining accuracy. Optionally, an

additional (16

) cycle can be activated for DAC mismatch

calibration or comparator offset calibration as shown later. All

the operations including the calibrations are asynchronously

controlled. Thus, only one relatively low-frequency sampling

clock f

is needed for both normal operation and calibration.

Fig. 3 shows the conversion scheme as well as the DAC of

the 13 b ADC. The 15 cycles include ten coarse cycles and

ﬁve ﬁne cycles, where the 7

and 11

cycle are the redundant

cycles. The ﬁrst redundant bit (7

cycle) relaxes DAC settling

time and facilitates the DAC mismatch calibration, which will

be explained later. Considering that the worst mismatch errors

happen for the largest capacitors, only the ﬁrst ﬁve DAC

capacitors are calibrated in this paper. The capacitors lower

than the redundant bit are not calibrated; thus, they need to be

sufﬁciently linear intrinsically. Thanks to the second redundant

bit (11

cycle), a two-mode comparator can be employed [14].

This redundancy allows, ﬁrst of all, the decision errors during

the coarse comparisons due to the comparator noise, thus

allowing a low-power mode comparator. Furthermore, since

the redundancy can tolerate the residual comparator offset

error after calibration as shown later, the comparator offset

calibration accuracy can be relaxed. The combination of

postcalibration comparator offset and coarse comparator noise

should remain within the redundancy range of the 11

bit,

which can tolerate errors up to ±8LSB.

B. Comparator Offset Error Detection

As mentioned earlier, the comparator works in the low-

power mode for the ﬁrst cycles (coarse cycles), and it

only switches to the low-noise mode with higher power for

the last few cycles (ﬁne cycles). In this way, the overall

power consumption of the comparator is reduced while it

still satisﬁes the noise requirement of the ADC. However,

the two-mode comparator will have two different offsets for

the corresponding two modes. Once this dynamic offset is

beyond the redundancy range (±8LSB), the ADC performance

cannot be recovered. Therefore, calibration of the dynamic

offset becomes necessary. The goal of the comparator offset

calibration is to minimize the offset difference V

delta

,which

equals V

off1

–V

off2

. Since a feedback loop [Fig. 1(b)] is used

to minimize V

delta

stepwise, rather than post processing, it is

sufﬁcient to detect the sign of V

delta

only in order to minimize

its value.

The comparator dynamic offset detection is shown in Fig. 4.

The equivalent voltage at the comparator input V

can be

viewed as a summation of the sampled input signal V

, DAC

reference voltage (V

DAC

), and the input-referred comparator

offset [V

off1(2)

]. The optional additional (16

) cycle is per-

formed on top of the 15-cycle comparison for a 13 b ADC.

The same comparison as the last (15

) cycle is repeated in

the additional (16

) cycle. The DAC code remains unchanged,

but the comparator switches from mode2 to mode1.Ideally,if

the two offsets are the same, the comparison result of the

last cycle (D

) and the additional cycle (D

) would be the

same. However, if the offsets are different, then the equivalent

剩余10页未读，继续阅读

nearbyboy

粉丝: 2
资源: 7

超低功耗13位6.4 MS/s SAR ADC：背景不匹配与偏置校准技术

0.6V低功耗10位1MS/s单调开关SAR ADC：0.13μmCMOS中的共模稳定器技术

节能型10位100 MS/s Flash-SAR混合ADC设计与优势

55nm CMOS异步SAR ADC：9.1ENOB 200MS/s图像传感器解决方案

具有基于梯形时域比较器的0.9V 2.72μW200 kS / s SAR ADC

具有背景失调校准的两路交错式7-b 2.4-GS / s 1-Then-2 b /周期SAR ADC

基于Flash-SAR架构的10位100-MS / s混合ADC

A 7b 2 GS/s Time-Interleaved SAR ADC with Time Skew Calibration Based on Current Integrating Sampler

具有55nm CMOS的混合单端/差分DAC的9.1ENOB 200MS / s异步SAR ADC，用于图像传感信号

采用0.18μmCMOS的10位20 kS / s 17.7 nW 9.1ENOB基准不敏感SAR ADC

SAR_ADC_SARADC-matlab_sar数据_SARADC_saradcmatlab_SARADC建模

最新资源