Two image encryption methods with hiding effect based on moiré pattern 3
Table 1 Superposing table for I
R
(x, y) and I
D
(x, y)
I
D
(x, y) = 0 I
D
(x, y) = 1
I
R
(x, y) = 0 0 1
I
R
(x, y) = 1 1 1
M
P
(x, y) = I
R
(x, y) ⊕ I
d
(x, y)
Example 1: Compute I
R
, I
D
and M
P
with the following S
according to formula (1) (λ = 2).
123456
000000
000000
111111
111111
010101
010101
010101
010101
010101
010101
101010
101010
010101
010101
111111
111111
R
D
P
s
I
I
M
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
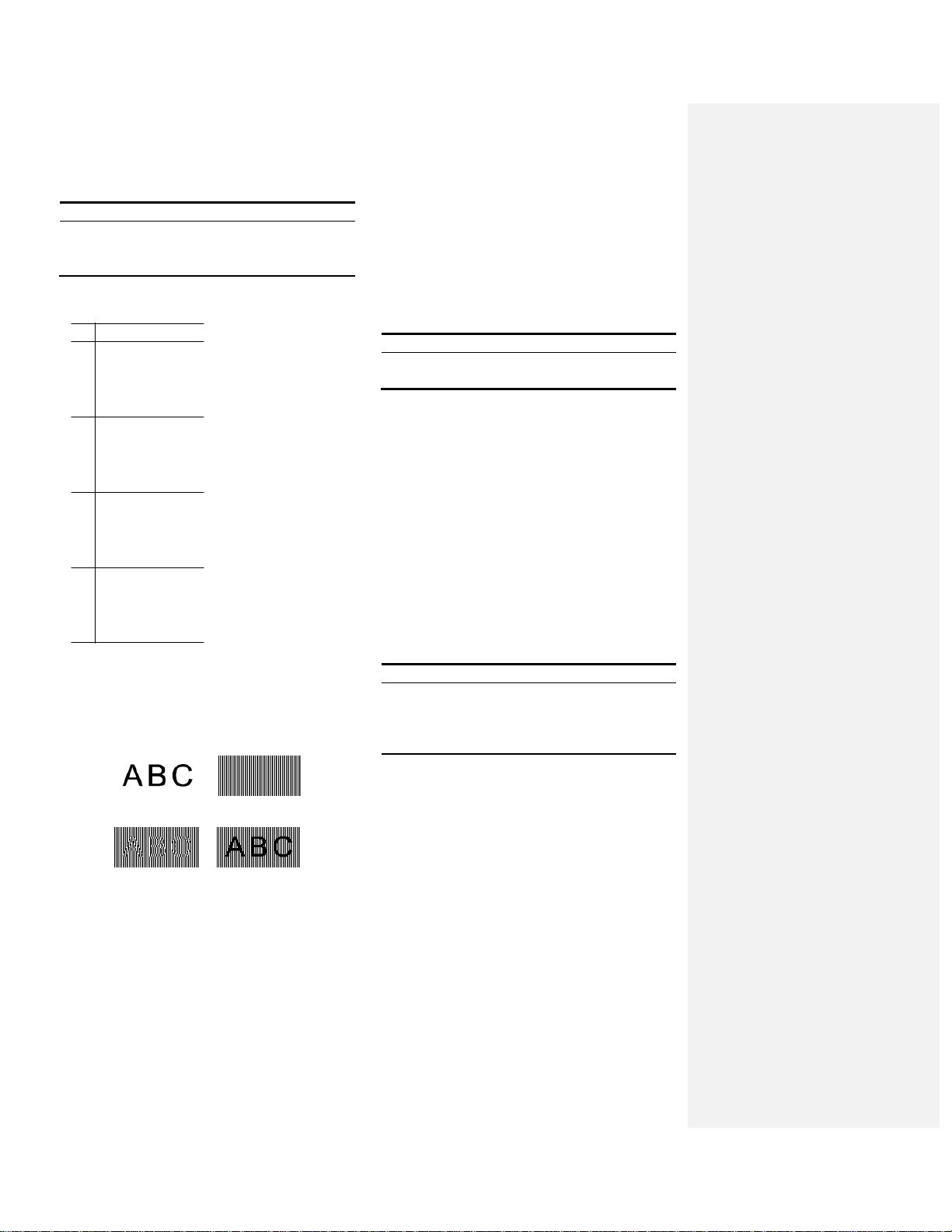
Figure 1 shows the procedures of image encryption method
based on formula (1) (λ = 2).
Figure 1 The procedures of image encryption method based on
formula (1) (λ = 2), (a) secret image S (size 128 × 64)
(b) reference layer I
R
(c) deformed layer I
D
(d) moiré
pattern, the superposition of I
R
and I
D
(a) (b)
(c) (d)
2.2 Motivation
The profile of the secret image can be observed in deformed
layer even with naked eyes [refer to Figure 1(c)]. Now we
analyse the root cause of leaking secret information in
deformed layer. Suppose S(x, y) ∈ {0, 1} and λ = 2. I
D
is
generated by deforming I
R
thus I
D
(x, y) can be represented
by I
R
(u, v). With different values of S(x, y), different
representations are listed in Table 2.
I
D
’s pixels, around the edge which corresponds to the
connection of black and white in S, have different phase
modulations. If an edge is approximately horizontal, the
lines above it mismatch with the lines below it. If an edge is
approximately vertical, the distance between the grating
lines will be closer or further compared with the normal
ones.
Thus, the secret image is leaked.
Table 2 Representations of I
D
(x, y) by I
R
(u, v)
S(x, y) I
D
(x, y)
0 I
R
(x, y)
1 I
R
(x–1, y)
In order to cover the leaking problem, we should scramble
the deformed layer while keeping the quality of moiré
pattern. Thus, the relationship between I
D
(x, y) and M
P
(x, y)
is provided in the following.
Let I
R
(1) (respectively, I
R
(0)) be the area which consists
of all black (respectively, white) pixels in I
R
; let I
D
[I
R
(1)]
(respectively, I
D
[I
R
(0)]) be the area in I
D
whose pixels have
the same positions with pixels in area I
R
(1) (respectively,
I
R
(0)).
Hence, I
D
can be divided into two separate sub-areas
I
D
[I
R
(0)] and I
D
[I
R
(1)].
In the two sub-areas, the values of I
R
(x, y), I
D
(x, y) and
M
P
(x, y) are shown in Table 3. Scrambling I
D
[I
R
(0)]
influences M
P
(x, y) and causes random noise in M
P
.
Scrambling I
D
[I
R
(1)] will not influence M
P
(x, y).
Table 3 Values of I
R
(x, y), I
D
(x, y) and M
P
(x, y) in sub-areas
of I
D
Area I
R
(x, y) I
D
(x, y) M
P
(x, y)
I
D
[I
R
(0)] 0 0 0
0 1 1
I
D
[I
R
(1)] 1 0 1
1 1 1
To make sure there is no random noise in M
P
, we scramble
area I
D
[I
R
(1)] to cover the leaking problem in this paper.
A straightforward attempt is to scramble I
D
[I
R
(1)]
directly, which utilises randomness to gain hiding effect.
Scrambling element, scrambling ratio and adjustment after
scrambling are considered together. Then, the first method
is proposed in Section 3.
An alternative attempt is rendering uniform distribution
in deformed layer, which can hide the secret image in
uniformity. Basic periodic structure and manners to get
uniform distribution are considered together. Furthermore,
meaningful image is shown in deformed layer. Then, the
second method is proposed in Section 4.



















