核技巧在支持向量机中的关键作用：解决非线性问题

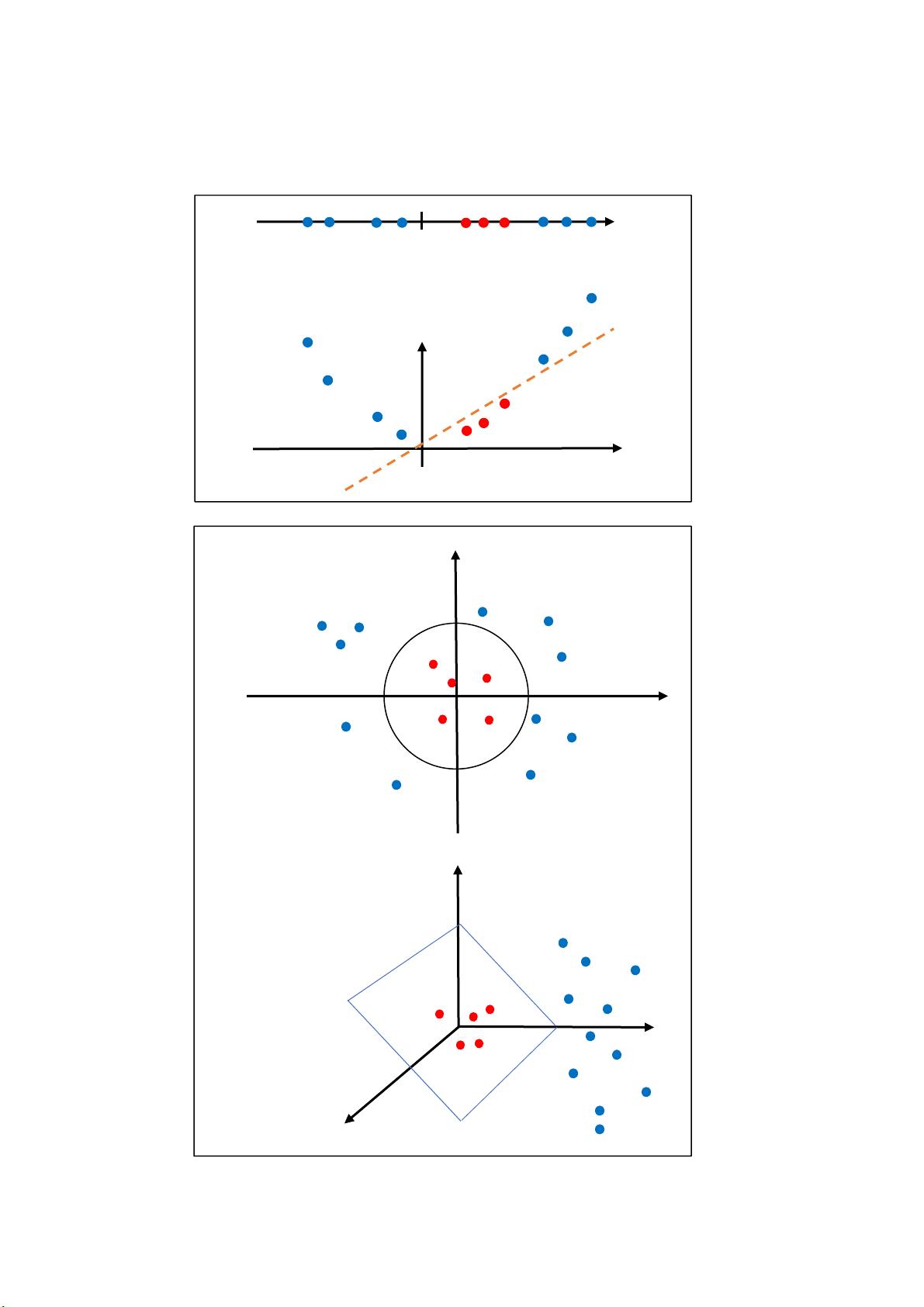
支持向量机（Support Vector Machine, SVM）是一种强大的监督学习算法，特别适用于处理非线性可分数据。在传统的SVM中，当输入特征无法通过线性超平面进行有效分类时，会遇到难题。这就是引入核函数（Kernel Trick）的原因，它使得SVM能够在高维空间中找到非线性决策边界。 核函数的核心思想是利用内积的性质，将原始低维空间的数据映射到一个更高维度的特征空间，使得原本线性不可分的数据在新的空间中变得线性可分。具体来说，给定一组输入变量$x_0, x_1, ..., x_n$，它们可能不是线性可分的，我们可以定义一个映射$φ(x)$，将原始特征$x$映射到特征空间$F$，其中$φ$通常是非线性的。在这个映射后的空间中，我们可以找到一个线性超平面来分割数据。 核函数$K(x_i, x_j) = φ(x_i)·φ(x_j)$充当了特征空间中的内积，我们并不需要知道实际的映射$φ$，只需要知道核函数值即可，这称为“核方法”。例如，常用的核函数包括线性核（$K(x_i, x_j) = x_i·x_j$）、多项式核（$K(x_i, x_j) = (γx_i·x_j + r)^d$）和径向基函数（RBF）核（$K(x_i, x_j) = \exp(-\gamma||x_i - x_j||^2)$），它们分别对应不同的数据拟合复杂度。 在核函数的帮助下，优化问题的形式发生了变化。原始的SVM目标函数变为在高维空间求解，但形式上保持不变，即最小化间隔$\frac{1}{2}\sum_{i=1}^{n}\alpha_i$，同时最大化软间隔$\sum_{i=1}^{n}\alpha_i - \sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jK(x_i, x_j)$，同时满足约束条件$\alpha_i \geq 0$和$\sum_{i=1}^{n}\alpha_iy_i = 0$。这里的$\alpha$是权重参数，$y_i$是类别标签。 通过求解拉格朗日函数的对偶问题，可以避免直接处理高维数据，简化计算。得到的最优解是支持向量（$\alpha_i > 0$对应的样本点），它们决定了决策边界的构建。最终，预测新样本$x$的类别是通过计算$x$在所有支持向量对应的超平面上的投影，并根据$K(x_i, x)$的值加权平均得到。 总结来说，核函数是支持向量机中的关键技术，它巧妙地解决了线性不可分问题，使SVM能够在复杂的非线性数据分布中建立有效的分类模型。通过对数据进行隐式高维变换，SVM能够在没有显式了解映射函数的情况下找到最佳决策边界，这使得SVM成为机器学习领域中的重要工具。