MATLAB求解偏微分方程:差分方法解析
需积分: 33 26 浏览量
更新于2024-09-12
收藏 1.28MB PDF 举报
本文主要介绍了如何使用MATLAB来求解偏微分方程,特别是针对热传导方程的差分方法,包括显式和隐式差分格式。
在MATLAB中解偏微分方程,通常采用数值方法,因为解析解往往难以获得,尤其是对于复杂的偏微分方程。这里重点讨论了差分法,它是一种常见的数值解法。差分法是通过将连续函数在空间和时间上离散化,将其转化为代数方程组来近似求解的方法。
1. 显式差分法:
显式差分法适用于时间步长满足稳定条件的情况。对于热传导方程 \(u_t = a^2 u_{xx}\),可以转化为以下差分形式:
\[ u(x,t+\Delta t) \approx u(x,t) + \Delta t \frac{a^2}{(\Delta x)^2} [u(x+\Delta x,t) - 2u(x,t) + u(x-\Delta x,t)] \]
这个公式表明,当前时刻的值可以通过上一时刻的值来计算。稳定条件要求 \(\Delta t \leq \frac{(\Delta x)^2}{2a^2}\),截断误差为 \(O((\Delta x)^2, \Delta t)\)。
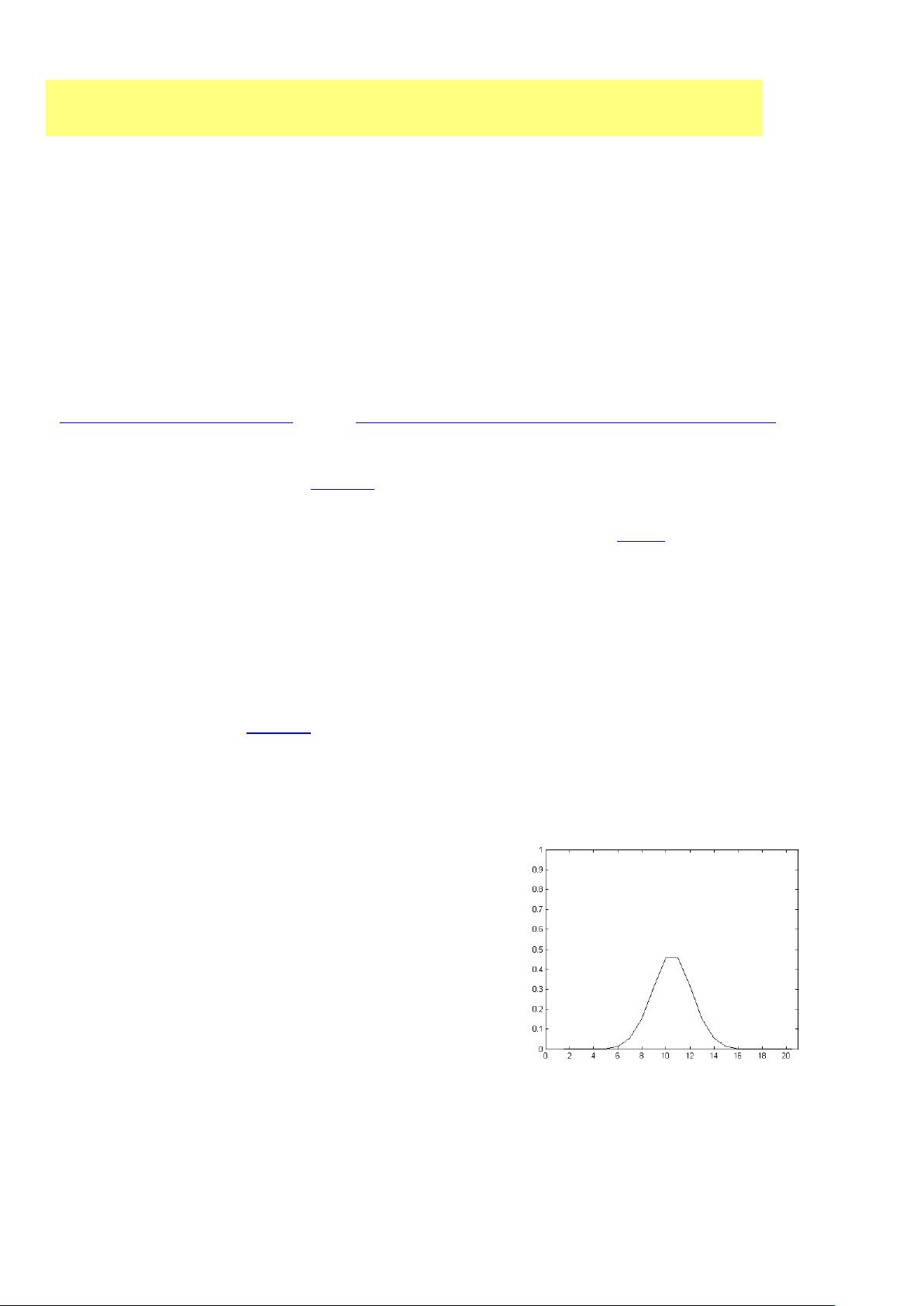
例如,对于一个长度为20单位、初始温度分布由函数 \(\phi(x)\) 给定的细杆传热问题,可以设定边界条件和时间步长,然后用循环结构进行迭代,计算每一时刻的温度分布。
2. 隐式差分法:
隐式差分法适用于更稳定的时间步长,但需要解决线性代数系统。对于热传导方程,可以得到如下差分形式:
\[ \frac{u(x,t+\Delta t) - u(x,t)}{\Delta t} \approx \frac{a^2}{(\Delta x)^2} [u(x+\Delta x,t+\Delta t) - 2u(x,t+\Delta t) + u(x-\Delta x,t+\Delta t)] \]
引入辅助变量 \(H\) 并重新排列,可以得到一个关于 \(u_{i,j+1}\) 的线性方程,然后通过求解线性系统找到 \(u_{i,j+1}\) 的值。
在MATLAB程序中,可以利用循环结构实现显式或隐式差分法,并通过`plot`函数实时显示温度分布的变化,或者使用`surf`函数生成三维表面图以直观地展示结果。这种编程方式对初学者来说既简单又直观,有助于理解偏微分方程的数值解法。
通过学习上述内容,读者将能够运用MATLAB进行偏微分方程的数值模拟,特别是在热传导问题中的应用。需要注意的是,选择适当的步长 \(\Delta t\) 和 \(\Delta x\) 对于保持数值稳定性至关重要,而隐式方法虽然增加了计算复杂性,但在允许更大的时间步长方面更具优势。
2013-05-31 上传
2024-07-20 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
2024-09-16 上传
2023-08-25 上传
magadlike
- 粉丝: 0
- 资源: 1
最新资源
- PureMVC AS3在Flash中的实践与演示:HelloFlash案例分析
- 掌握Makefile多目标编译与清理操作
- STM32-407芯片定时器控制与系统时钟管理
- 用Appwrite和React开发待办事项应用教程
- 利用深度强化学习开发股票交易代理策略
- 7小时快速入门HTML/CSS及JavaScript基础教程
- CentOS 7上通过Yum安装Percona Server 8.0.21教程
- C语言编程:锻炼计划设计与实现
- Python框架基准线创建与性能测试工具
- 6小时掌握JavaScript基础:深入解析与实例教程
- 专业技能工厂,培养数据科学家的摇篮
- 如何使用pg-dump创建PostgreSQL数据库备份
- 基于信任的移动人群感知招聘机制研究
- 掌握Hadoop:Linux下分布式数据平台的应用教程
- Vue购物中心开发与部署全流程指南
- 在Ubuntu环境下使用NDK-14编译libpng-1.6.40-android静态及动态库