斯坦福CS229机器学习课程：线性代数与概率论笔记

本文档是关于机器学习的学习笔记，涵盖了斯坦福大学CS229课程的复习材料，包括线性代数和概率论的基础知识。资料包含文档和PPT，适合学习者共同学习讨论。 在机器学习领域，线性代数和概率论是不可或缺的数学基础。线性代数主要涉及向量、矩阵以及它们之间的运算，而概率论则提供了处理不确定性事件的理论框架。以下是这些主题的详细阐述： 1. 线性代数基础 - 线性方程组的表示：线性代数通过矩阵形式简化了多变量方程组的表示，便于计算和分析。例如，矩阵乘法可以紧凑地表示线性方程组，使得操作更为便捷。 - 基本符号：矩阵用大写字母表示，如；向量用小写字母表示，如。向量的第i个元素记作；矩阵的元素记作或。 - 矩阵乘法：两个矩阵相乘时，需满足内宽外长的规则，即第一个矩阵的列数必须等于第二个矩阵的行数。 2. 向量和矩阵的运算 - 内积（点积）：两个向量的内积给出一个标量结果，表示向量在特定方向上的投影。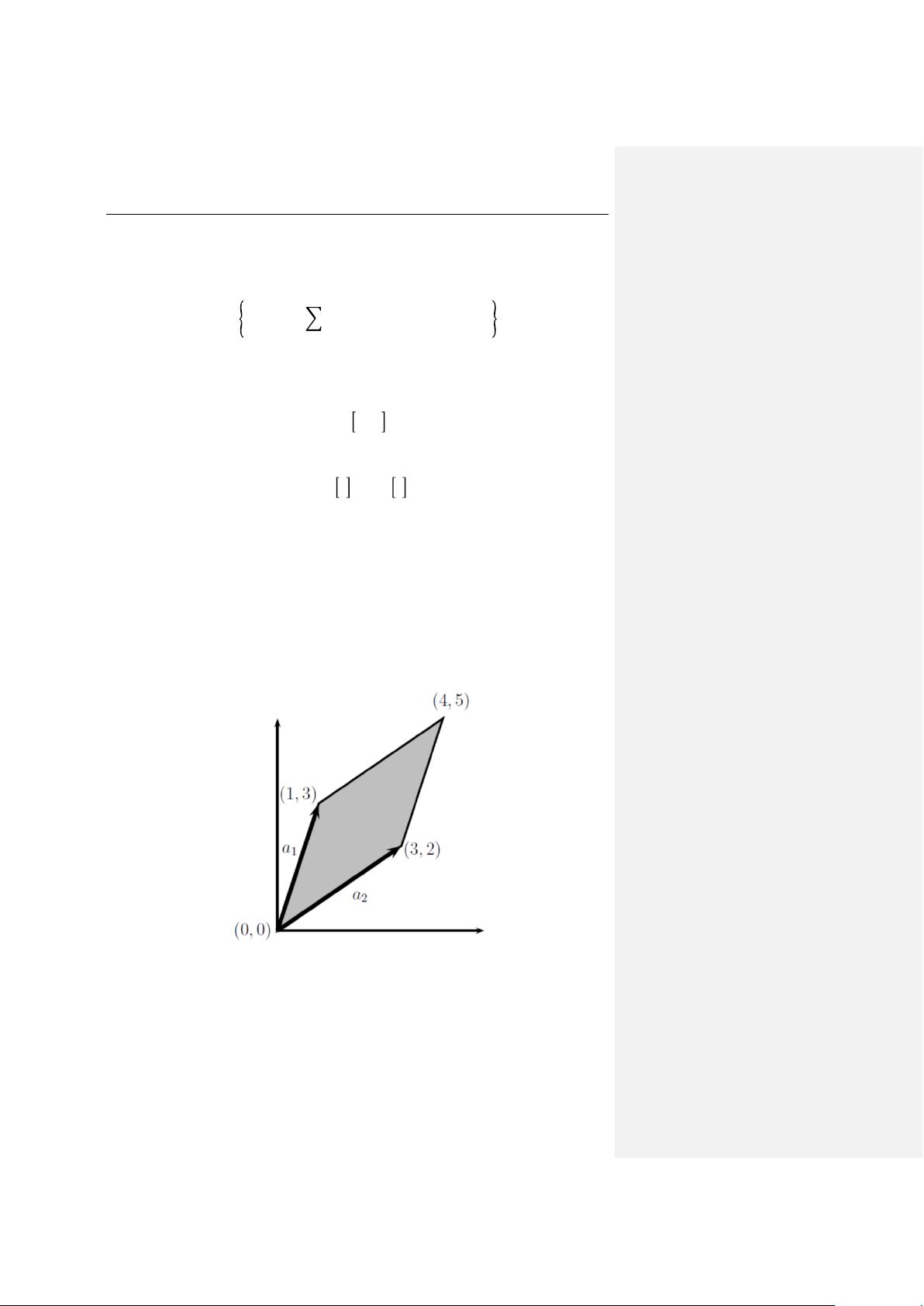 - 外积：向量的外积生成一个新的矩阵，当两个向量同维时，结果是一个二维矩阵，即它们的外积构成的张量。 - 矩阵-向量乘法：矩阵乘以向量得到一个新的向量，这是线性变换的一种表达方式，常用于机器学习模型的参数更新。 3. 概率论基础 - 基本要素：概率论涵盖事件、样本空间、概率分布等概念，用于量化不确定性。 - 随机变量：随机变量是可能取不同值的量，其概率分布描述了每种取值的可能性。 - 两个及以上随机变量：联合分布描述两个或多个随机变量同时出现的概率，边缘分布和条件分布分别描述单个变量的概率和在已知其他变量情况下的概率。 这些基础知识对理解机器学习算法至关重要。例如，线性代数在支持向量机（SVM）、主成分分析（PCA）等算法中起到关键作用，而概率论则是贝叶斯网络、马尔科夫随机场（Markov Random Field）等模型的基础。深入掌握这些概念和运算，有助于更有效地理解和实现各种机器学习算法。