四元数与三维旋转的直观解析与MATLAB实现

本篇文章深入探讨了四元数（Quaternion）在三维旋转中的应用，作者试图提供一种基于几何学和线性代数的直观理解，以便于计算机图形学和相关领域的读者。不同于网上的许多代数化讲解，文章强调的是四元数与3D旋转的几何关联，而不是抽象的数学理论。 首先，文章从复数（Complex Number）的概念和性质入手，指出四元数与复数有许多相似之处，了解复数的基本概念如实部和虚部、复数的线性表示形式（即复平面上的向量表示），有助于更好地理解四元数。作者提到了复数可以表示为 \( z = a + bi \)，其中 \( a \) 是实部，\( b \) 是虚部，且 \( i^2 = -1 \)。 接下来，文章通过将复数看作是向量 \( \begin{pmatrix} a \\ b \end{pmatrix} \) 的形式，展示了复数如何与2D旋转关联，这为后续讨论三维空间中的旋转奠定了基础。作者提到，由于四元数与复数类似，这些基本的几何思想可以被扩展到三维，特别是通过引入额外的分量来表示旋转。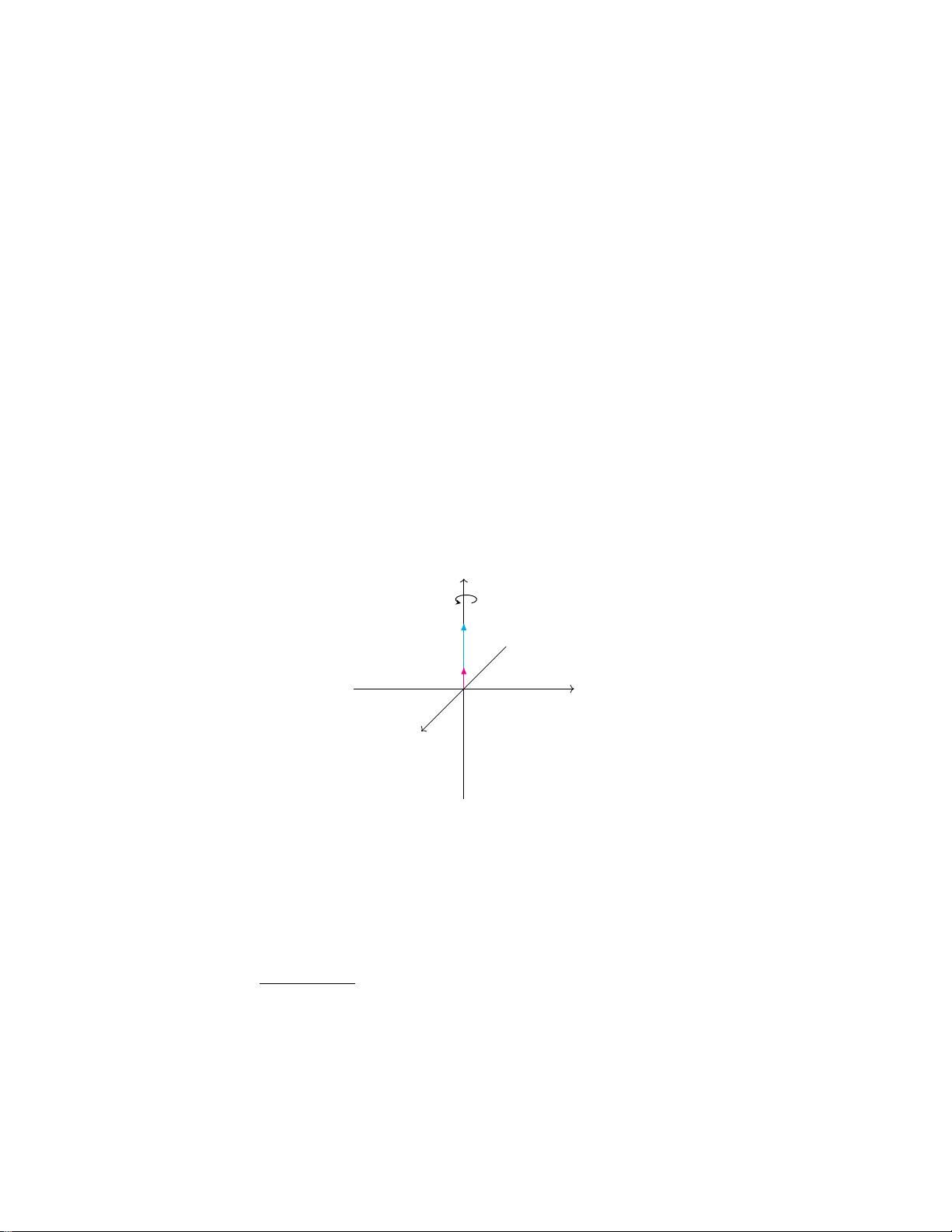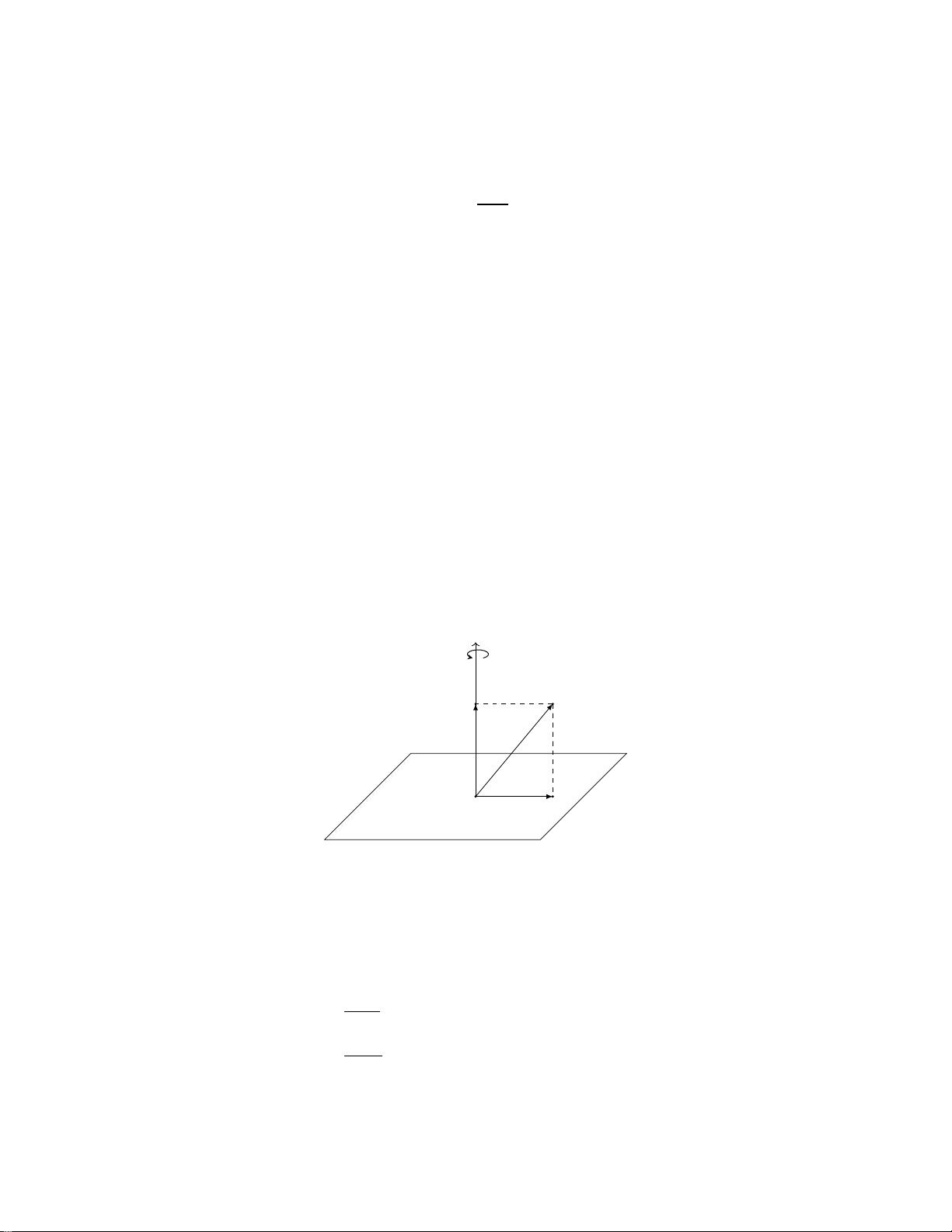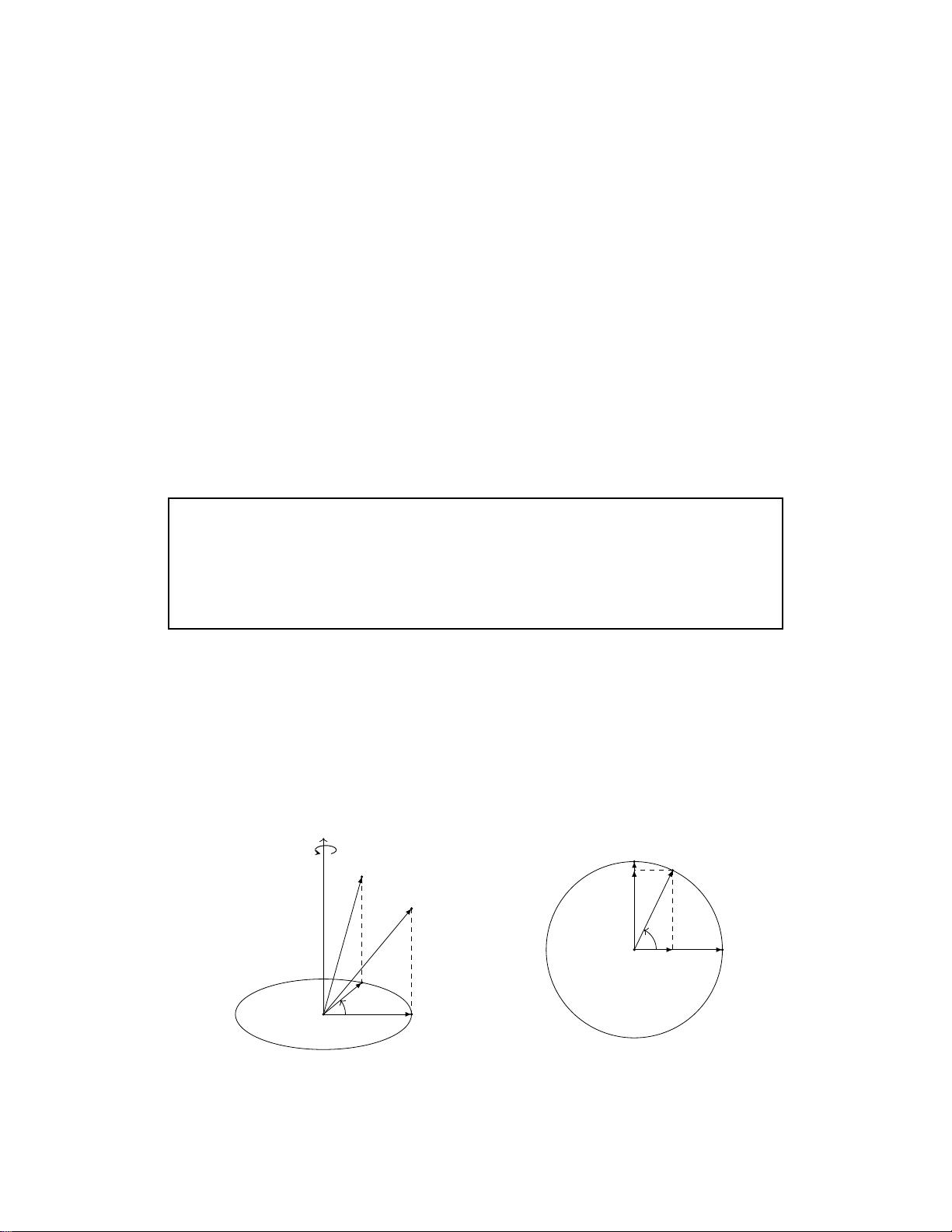 在主体部分，作者重点阐述了四元数的构造和与三维旋转的关系。四元数通常表示为 \( q = w + xi + yj + zk \)，其中 \( w \) 代表实部，而 \( x, y, z \) 分别对应三维空间中的三个正交轴。四元数不仅能够紧凑地表示旋转角度，还能同时处理旋转中心和旋转轴，这是标准三维旋转矩阵无法做到的。通过分解四元数，可以方便地进行旋转的加法和复合，这对于计算机图形学中的旋转变换操作至关重要。 尽管文章针对的是计算机图形学的应用背景，但对于物理学家或抽象代数研究者，部分内容可能不够深入。然而，文章结尾推荐了一些拓展阅读材料，可以帮助他们从不同角度理解四元数。作者还分享了MATLAB/Octave代码示例和动画，以及关于版权的规定，鼓励读者在遵循协议的前提下进行交流和学习。 这篇文档提供了四元数在三维旋转中的实用性和直观解释，通过与复数的类比，使读者能更好地掌握这种重要的数学工具在计算机图形学领域的实际应用。