三角函数图形与性质全览：公式与图解

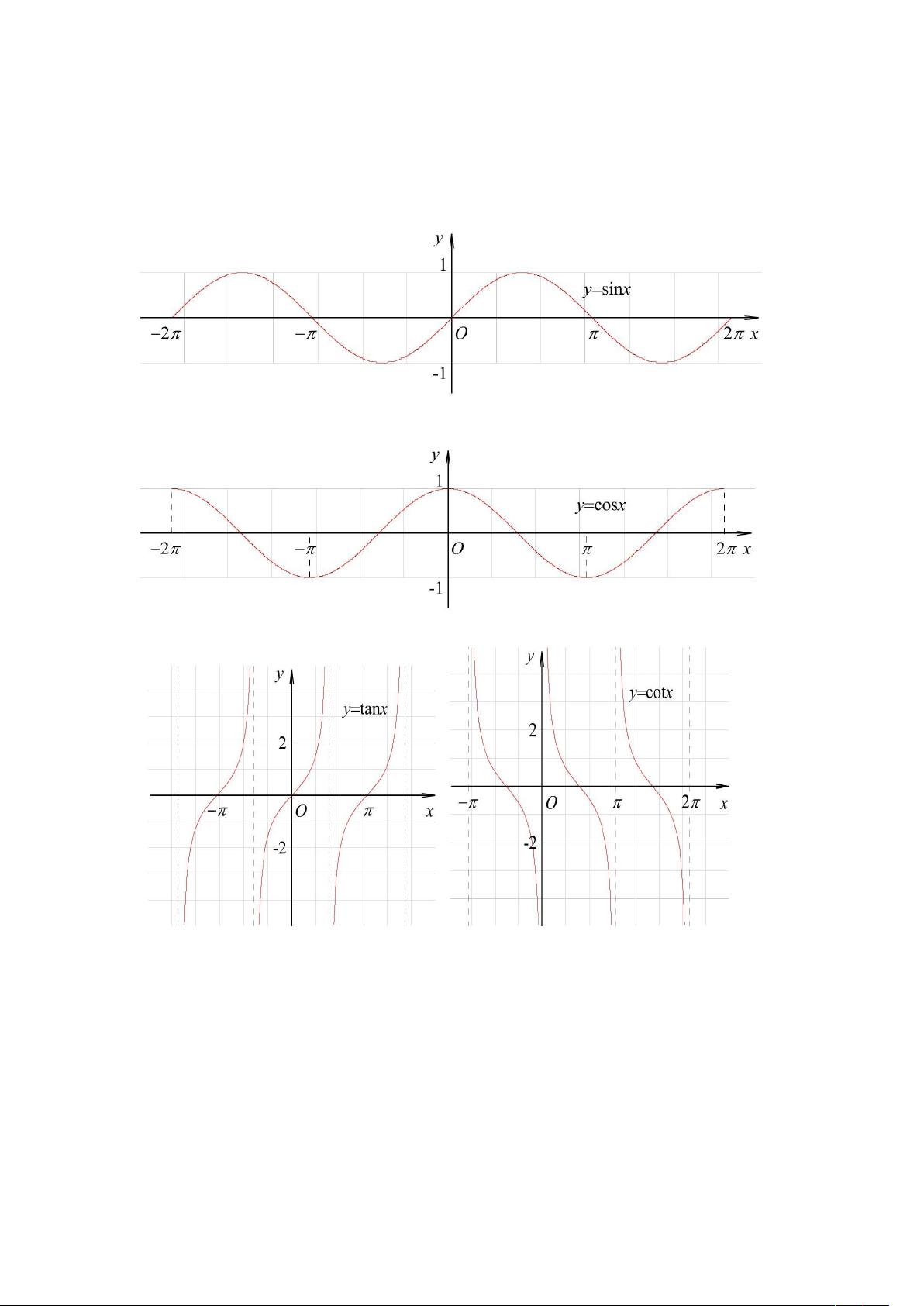
本资源提供了一套全面的三角函数公式、图像和特性概述，旨在帮助学习者深入理解和掌握数学中的三角函数概念。以下是主要知识点的详细解析： 1. **三角函数图形**： - **幂函数**: 提供了幂函数的图形示例，包括正指数和负指数函数的图像，展示了不同幂次函数的变化趋势和零点分布。 - **指数函数**: 包括了指数函数的基本图形，重点展示了函数的增减性和周期性。 - **对数函数**: 对数函数的图像通常与指数函数相对应，展示对数函数的定义域、值域和单调性。 - **三角函数**: 该部分集中于正弦、余弦、正切和余切函数的图形，包括它们在各个象限内的符号变化以及函数的周期性和奇偶性。 - **各三角函数值的符号**: 详细列出了每个函数在各个象限内函数值的符号规则。 2. **三角函数性质**： - **定义域**: 说明了每种三角函数的定义域，例如正弦函数在整个实数集R上定义，但除了一些特殊点外。 - **值域**: 指出函数的最大值和最小值，如正弦函数的最大值和最小值分别为1和-1。 - **周期性**: 强调了三角函数的周期性，如正弦和余弦函数的周期为2π，而正切和余切函数的周期为π。 - **奇偶性**: 说明了各函数的奇偶性，如正弦是奇函数，余弦是偶函数。 - **单调性**: 描述了函数在特定区间内的单调性，如正弦函数在特定区间内的增减性。 3. **反三角函数**： - **反三角函数图形**: 提供了反正弦、反余弦、反正切和反余切函数的图像，这些是原三角函数的逆运算，用于求解特定角度的三角函数值。 - **反三角函数的性质**: 定义了反三角函数的名称和用途，比如反正弦函数（arcsin）表示求出某个角度的正弦值，反余切函数（arccot）表示求出某个比例的反正切值。 通过这份资料，学习者可以系统地掌握三角函数的基础理论，通过图形直观地理解其行为，并能够运用反三角函数进行实际问题的求解。无论是初学者还是进阶学生，这份资源都将是一个宝贵的参考资料。