1322 IEEE TRANSACTIONS ON COMPONENTS, PACKAGING AND MANUFACTURING TECHNOLOGY, VOL. 5, NO. 9, SEPTEMBER 2015
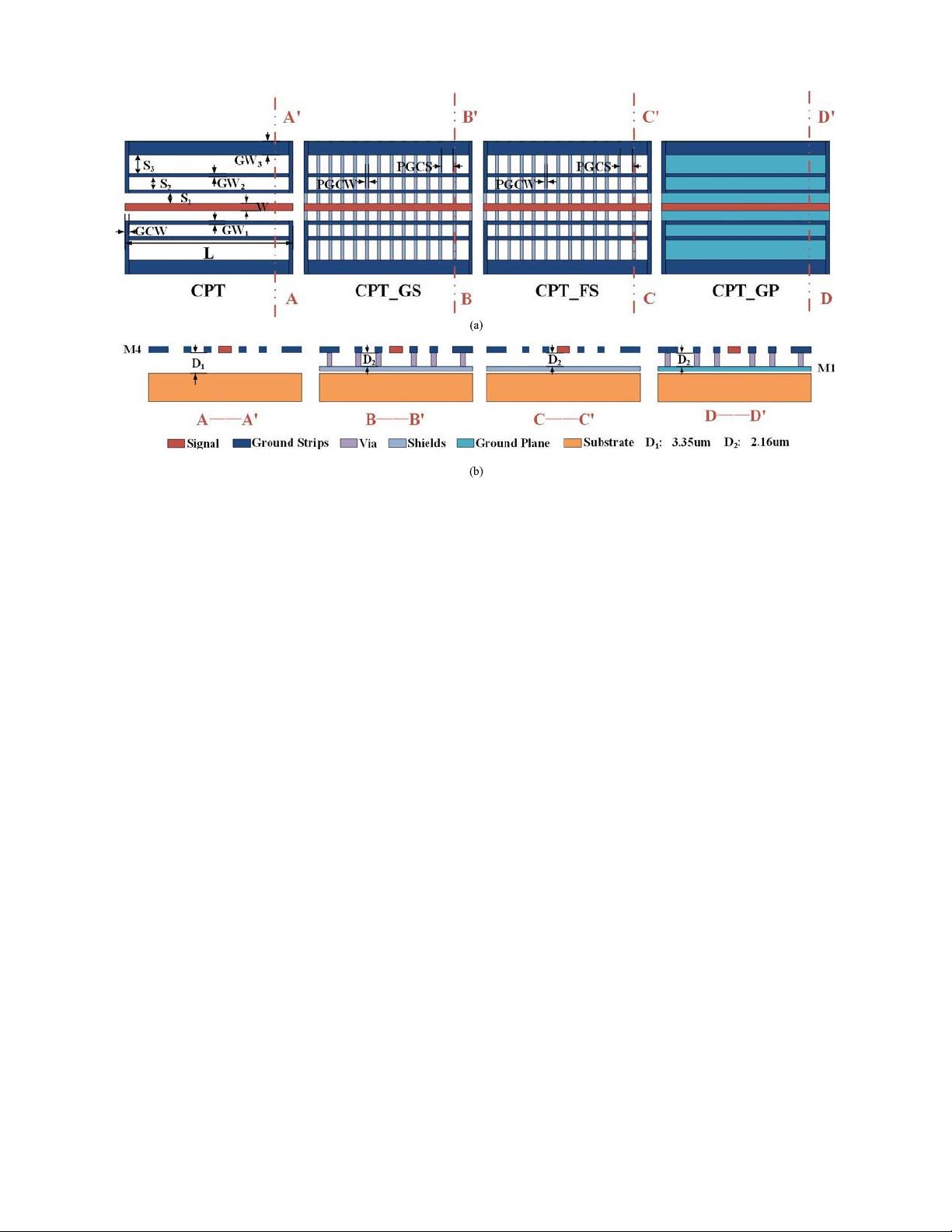
Fig. 2. Top views and cross sections of interconnects. (a) Top views. (b) Cross sections.
III. QUALITATIVE ANALYSIS OF CURRENT RETURN PATHS
The RLCG model consists of four distributed transmission
lines parameters, R, L, C,andG, which are shown to be
frequency dependent. Incorporated with the methods
introduced in [15], the four frequency-dependent parameters
can be directly extracted from telegrapher’s equations. The
RLCG distributed circuits model in the frequency domain can
precisely represent the frequency behavior of the transmission
lines. Moreover, the variations of these four parameters
with the increment of frequencies pretty much depend on
the distribution of current return paths. Hence, qualitative
analysis of the RLCG parameters will provide sufficient
intuitive insights of various current return path effects, which
are beneficial to the model setup of the interconnect.
On the basis of telegrapher’s equations, the RLCG parame-
ters can be obtained from measured S-parameters, as shown
in Fig. 3. By the way, the large variation of RLCG parameters
of CPT_GS is owing to the discontinuity of the spectrum
spread module. Since the Vector Network Analyzer (VNA)
can just measure the S-parameters directly up to 67 GHz, we
need the spectrum spread module to get the measurements
from dc to 100 GHz. In addition, the measurements from
dc to 67 GHz are still accurate and are able to describe the
practical behavior of CPT_GS.
A. Equivalent Resistance
At low frequencies, all of the equivalent resistances
are around 2 , but they gradually increase to about
10 at 60 GHz. As for the loss mechanisms described in [24],
the skin effects and proximity effects will be distinguished
at high frequencies, resulting in the reduction of the conduc-
tor’s effective transverse current. Thus, the ohmic loss will
be enlarged. Besides, all the equivalent resistance of these
interconnects are the same during the entire frequency range.
That is, the distribution of various current return paths has
minor effects on the equivalent resistances.
B. Equivalent Inductance
The changing trends of the four equivalent inductances are
in a similar manner as shown in Fig. 3(b). On one hand, the
inductance will dominate the impedance of the series branch
at high frequencies compared with the resistance. And smaller
the size of the current loop is, the smaller the inductance is.
As we all know, the current always prefer the paths with
least impedance. Therefore, more currents will take the ground
conductors that are close to the signal line as return paths,
reducing the size of current loops and, certainly, the equivalent
inductances. Similarly, the skin and proximity effects also
contribute to the above circumstance. On the other hand,
from the point of energy transformation, there is more energy
stored in electric fields due to the strengthened shunt parasitic
capacitances at high frequencies. Thus, the energy stored in
magnetic fields would be reduced, resulting in the decrement
of equivalent inductances.
In addition, compared with CPT, CPT_GS, and CPT_FS,
the equivalent inductance of CPT_GP is relatively smaller.
As shown in Fig. 2(b) and Table I, the distance between the
signal line and the ground metal plane is much smaller than
the one between the signal line and the coplanar grounded
metal strips. Therefore, electrical coupling is much stronger
between the signal line and the ground plane. Thus, the ground
plane serves the major current return path in CPT_GP. On the
other hand, the situation in the other three interconnect is quite
different. The shields in CPT_GS, CPT_FS are designed to
prevent electrical coupling from the signal line to the substrate.
Moreover, the return current in the shields is much smaller due
to the patterned structure. Thus, the coplanar metal ground









