EWT算法详解与EMD比较：实证小波变换的理论增强

需积分: 17 152 浏览量更新于2024-07-18 收藏 2.46MB PDF 举报

本文档主要关注Empirical Wavelet Transform (EWT)的相关研究，它是一种在信号处理领域备受关注的方法，特别是与Empirical Mode Decomposition (EMD)进行对比。EWT旨在根据信号中包含的信息来分解信号，其适应性强，适合于多种应用。然而，EWT的主要挑战在于缺乏坚实的理论基础，这限制了其在某些领域的广泛应用。文章标题《Empirical Wavelet Transform》发表于2013年8月的《IEEE Transactions on Signal Processing》，DOI为10.1109/TSP.2013.2265222，作者Jerome Gilles来自San Diego State University。该文的发表引起了266次引用和2,090次阅读，显示出其在学术界的影响力。Jerome Gilles还参与了其他相关的项目，如“Imaging Through Atmospheric Turbulence”和“Multicluster thresholding of unimodal histogram”。文章的核心内容集中在对EWT算法的详细介绍，强调了它如何通过非线性方式捕捉信号中的局部特征和趋势，不同于传统的滤波方法。与EMD相比，EWT的优势可能在于它的灵活性和对复杂信号的更好适应性，尽管EMD的理论基础相对薄弱。作者试图弥补这一不足，提出了一种新的构建适应性方法，这可能涉及到改进的分解策略或者理论框架的扩展。在文章中，作者可能会讨论EWT的具体步骤、分解过程中的关键参数选择、以及如何通过数学模型确保其有效性。此外，可能还包含了实证分析和案例研究，展示了EWT在实际信号处理任务中的性能和优势。总而言之，这篇文献对于理解EWT的原理、它与EMD的区别，以及如何在没有强大理论支撑的情况下发展这种技术具有重要的参考价值。对于那些在信号处理，尤其是适应性和细节分析方面寻求创新解决方案的研究人员和工程师来说，这篇文章是深入学习和进一步研究的重要资源。

2 IEEE TRANS. ON SIGNAL PROCESSING, VOL. XX, NO. XX, FEBRUARY 2013

0.2

0.4

0.6

0.8

1.0

-2

0.2

0.4

0.6

0.8

1.0

-1.0

-0.5

0.5

1.0

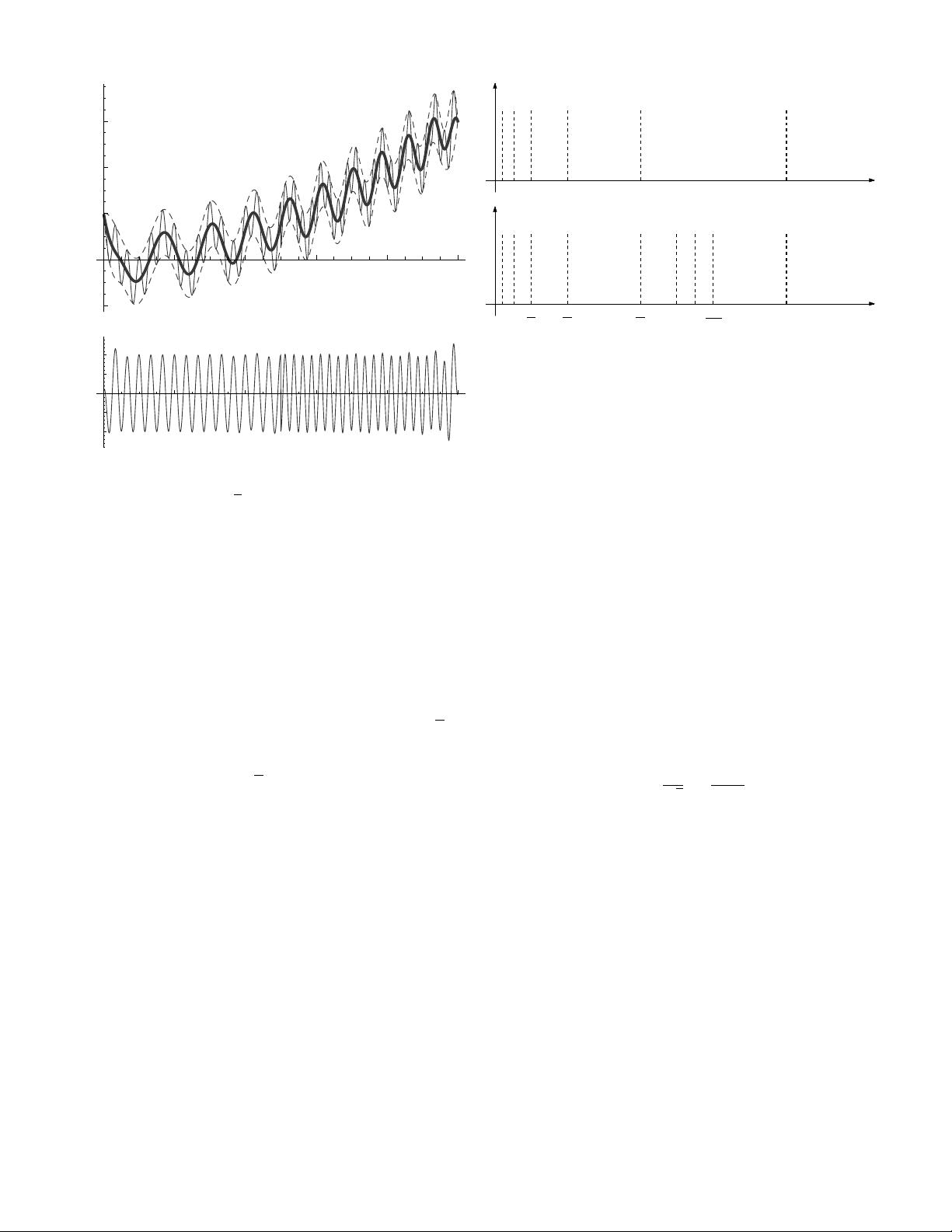
Fig. 1. EMD: basic IMF detection. Envelopes detection on top (thin

continuous: f , dashed:

f and f and thick continuous: m). On bottom: the

ﬁrst IMF candidate r

An IMF is an amplitude modulated-frequency modulated

function which can be written in the form

(t) = F

(t) cos (ϕ

(t)) where F

(t), ϕ

(t) > 0 ∀t.

(2)

The main assumption is that F

and ϕ

vary much slower

than ϕ

. The IMF f

behaves as a harmonic component.

Originally, the method of Huang et al. [9] to extract such

IMFs is a pure algorithmic method. Candidates for an IMF are

extracted by ﬁrst computing the upper,

f(t), and lower, f(t),

envelopes via a cubic spline interpolation from the maxima

and minima of f. Then the mean envelope is obtained by

computing m(t) = (

f(t) + f(t))/2 and ﬁnally the candidate

by r

(t) = f(t) − m(t) (see Fig. 1). Generally, r

(t) does

not fulﬁll the properties of an IMF. A good candidate can be

reached by iterating the same process to r

and the subsequent

. The ﬁnal retained IMF is f

(t) = r

(t). Then the next IMF

is obtained by the same algorithm applied on f(t)−f

(t). The

remaining IMFs can be computed by repeating this algorithm

on the successive residues.

The interesting fact about this algorithm is that it is highly

adaptable and is able to extract the non-stationary part of

the original function. However, its main problem is that it is

based on an ad-hoc process which is mathematically difﬁcult

to model. Consequently it is difﬁcult to really understand

what the EMD provides. For example, some problems appear

when some noise is present in the signal. To deal with this

problem, an Ensemble EMD (EEMD) was proposed in [17].

The authors propose to compute several EMD decompositions

of the original signal corrupted by different artiﬁcial noises.

Then the ﬁnal EEMD is the average of each EMD. This

approach seems to stabilize the obtained decomposition but

it increases the computational cost.

Another EMD approach is proposed in [8]. The authors

π/2

π/4

π/8

. . .

3π

. . .

Fig. 2. On top: dyadic wavelet tiling of the frequency line. On bottom: a

wavelet packet like tiling.

proposed to minimize a functional which looks for a sparse

representation of f in a dictionary of IMFs. This variational

method provides similar results as the original EMD algorithm.

However, this functional is based on a scheme which uses

higher order total variation terms, this makes the method

sensitive to the presence of noise and some ﬁltering must be

added to the method.

B. Wavelets approaches

Nowadays, wavelet analysis is one of the most used tool in

signal analysis. Let us ﬁx some notations and recall the very

basics about wavelet theory. For further details, we refer the

reader to the extensive literature about the wavelet theory, see

for example [3], [10], [12], [14]. The Fourier transform and

its inverse are denoted

f and

f, respectively. In the temporal

domain, a wavelet dictionary {ψ

u,s

} is deﬁned as the dilated,

with a parameter s > 0, and translated by u ∈ R of a mother

wavelet ψ (of zero-mean) as

u,s

(t) =

√



t − u



. (3)

Then the wavelet transform of f is obtained by computing

the inner products W

(u, s) = hf, ψ

u,s

i. If s is a continuous

variable then W

(u, s) is called the continuous wavelet trans-

form while if s = a

then W

(u, s) = W

(u, j) is called the

discrete wavelet transform. A useful property of the wavelet

transform is that it can be viewed as the application of a ﬁlter

bank (each ﬁlter corresponds to one scale). In practice, the

most used case is the dyadic case, s = 2

. It can be shown

that such a case corresponds to tile the time-frequency plane

like in top of Fig. 2.

As we are interested in developing adaptive representations,

we recall some existing tentatives of adaptive wavelets con-

struction. As far as we know there are a very few attempts in

the literature. Probably the most known method is the wavelet

packets in a basis pursuit framework based on successive scale

reﬁnements of the expansion. It provides an adaptive time-

frequency plane tiling like in bottom of Fig. 2. Even though

the wavelet packets are useful in many applications, they use

a constant prescribed ratio in the subdivision scheme, which

剩余14页未读，继续阅读

miracleso0h

粉丝: 1
资源: 1

EWT算法详解与EMD比较：实证小波变换的理论增强

利用EWT方法在Matlab中提取故障特征

基于LZW压缩的MATLAB EWT信号特征提取

EWT经验小波变换的Matlab源码实现

经验小波（Empirical wavelet transform）第四版的工具箱以及作者的三篇参考文献

EWT 经验小波变换matlab源程序

基于EWT的电力系统低频振荡参数辨识方法分析.pdf

MATLAB经验小波变换（EWT）工具箱的安装与使用

【数字信号分解】基于matlab经验小波变换EWT数字信号分解【含Matlab源码 期】.zip

Python实现经验小波变换：EWT包详细解析

基于Flask，mysql slope one的图书推荐系统全部资料+详细文档.zip

最新资源

【数字信号分解】基于matlab经验小波变换EWT数字信号分解【含Matlab源码期】.zip