组合逻辑电路分析：从BCD码到表决电路

"常见BCD码一览表-数字电子技术CH2（机电32学时）" 在数字电子技术中，BCD码（Binary-Coded Decimal，二进制编码的十进制）是一种用于将十进制数转换为二进制数的方法。这种编码方式允许我们用二进制系统来表示十进制数，使得数字处理和计算更加方便。本资源主要关注几种常见的BCD码类型。 首先，余3码是一种BCD码，它的特点是将8421BCD码加上0011来得到一个满足BCD规则的编码。8421BCD码是最基础的有权BCD码，其中每一位二进制码元都对应着一个确定的位权值，分别为8、4、2、1，这使得我们可以直接通过位权展开计算出它所代表的十进制数。例如，十进制数5的8421BCD码是0101。 有权BCD码的其他变种包括2421码和5121码，它们同样遵循每位二进制位对应一个位权的原则，只是位权值不同。2421码中，每一位的位权依次是2、4、2、1，而5121码则使用5、1、2、1作为位权。这些码型的设计目的是为了简化十进制数到二进制数的转换和计算过程。 第二章组合逻辑电路是数字电子技术的重要组成部分，主要探讨电路如何处理逻辑输入并产生逻辑输出，而不考虑之前的电路状态。组合逻辑电路有以下特点： 1. 任何时刻的输出仅取决于当前的输入信号，不依赖于电路的前一状态。 2. 组合逻辑电路没有反馈通路，即信号不会从输出端回流到输入端。 3. 电路中不含记忆单元，如触发器或寄存器。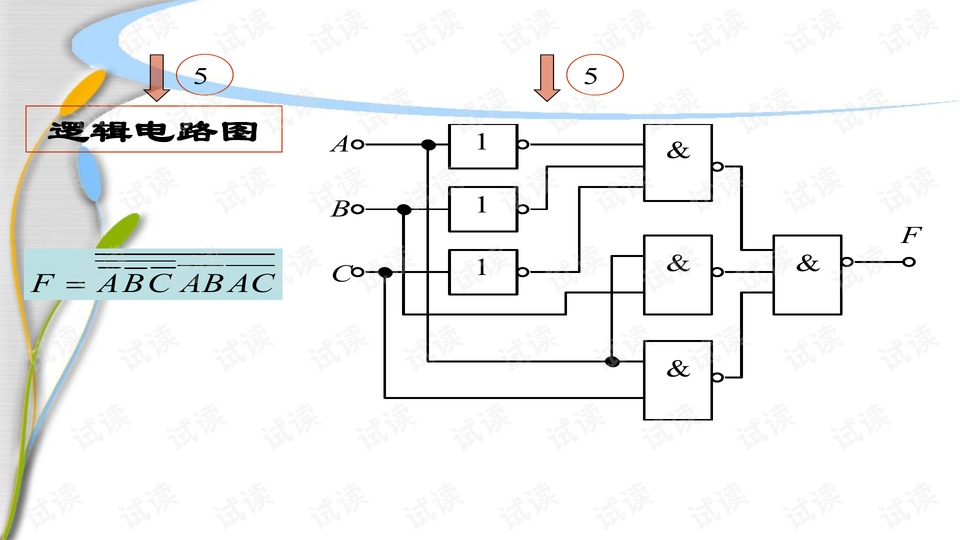 在组合逻辑电路的分析中，我们通常会通过以下步骤确定其逻辑功能： 1. 从逻辑图中写出输出的逻辑表达式，这通常涉及从输入端开始逐级推导。 2. 化简逻辑表达式，以获得最简的与或表达式，这有助于减少实现该功能所需的逻辑门数量。 3. 列出真值表，根据最简表达式来显示所有可能的输入/输出组合。 4. 描述逻辑功能，基于真值表总结电路的总体行为。 设计组合逻辑电路则涉及到根据特定的逻辑需求，反向推导出实现该功能的最简逻辑门网络。例如，可以通过分析问题，使用布尔代数和化简技巧，设计出实现特定逻辑运算（如加法、比较、表决等）的电路。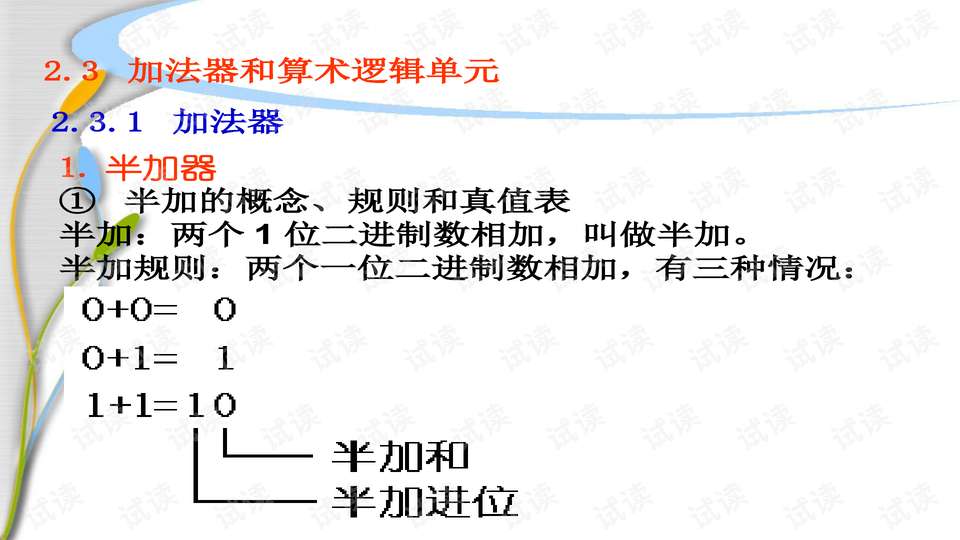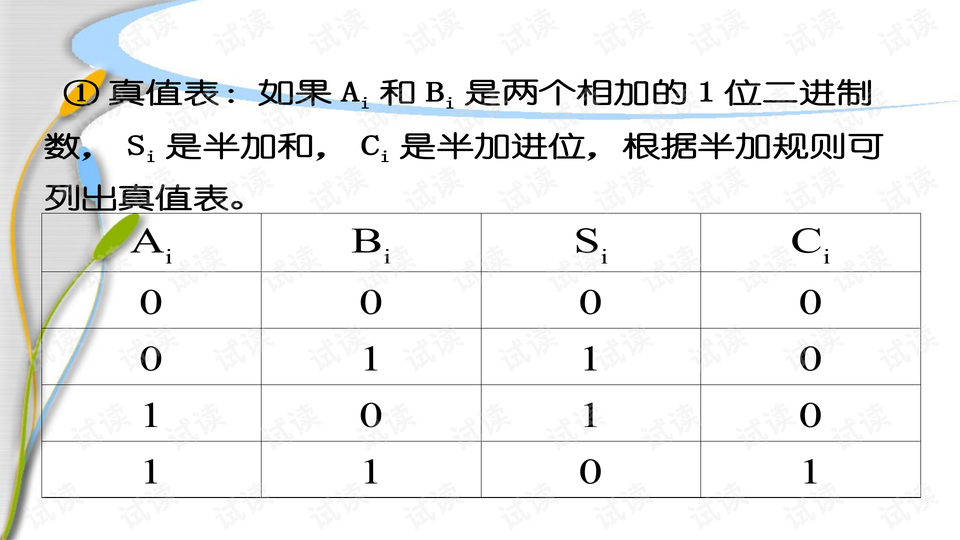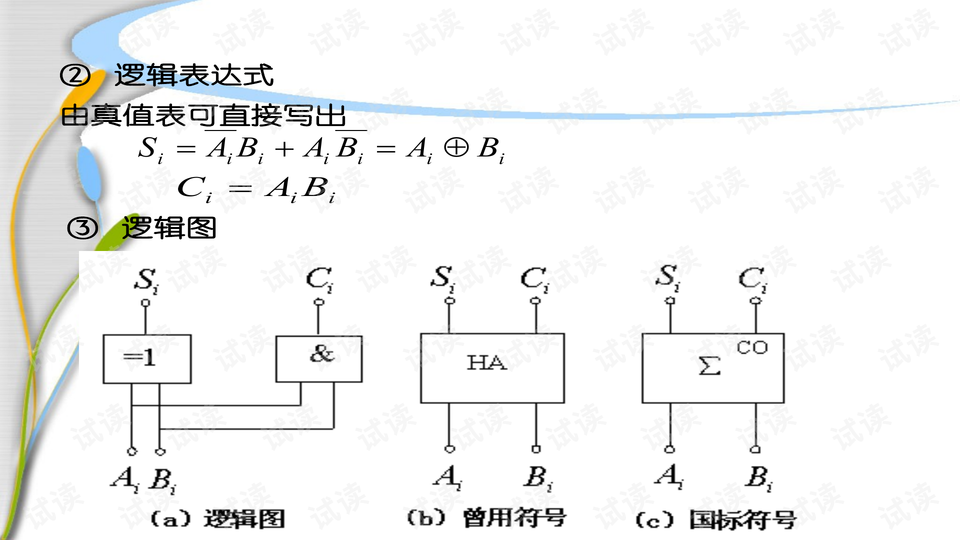 在实际应用中，中规模集成电路（MSI）常被用来构建组合逻辑电路，它们提供了预定义的功能，如加法器、算术逻辑单元（ALU）、数值比较器、译码器、数据选择器等。了解这些元件的功能和使用方法是进行数字系统设计的基础。 本资源涵盖了数字电子技术中的关键概念，包括BCD码和组合逻辑电路的分析与设计，对于学习和理解数字电路的工作原理至关重要。通过深入学习这部分内容，学生将能够设计和分析各种组合逻辑电路，以及有效地将十进制数转换为二进制数。