信息论实验指导：信源编码与信道容量计算

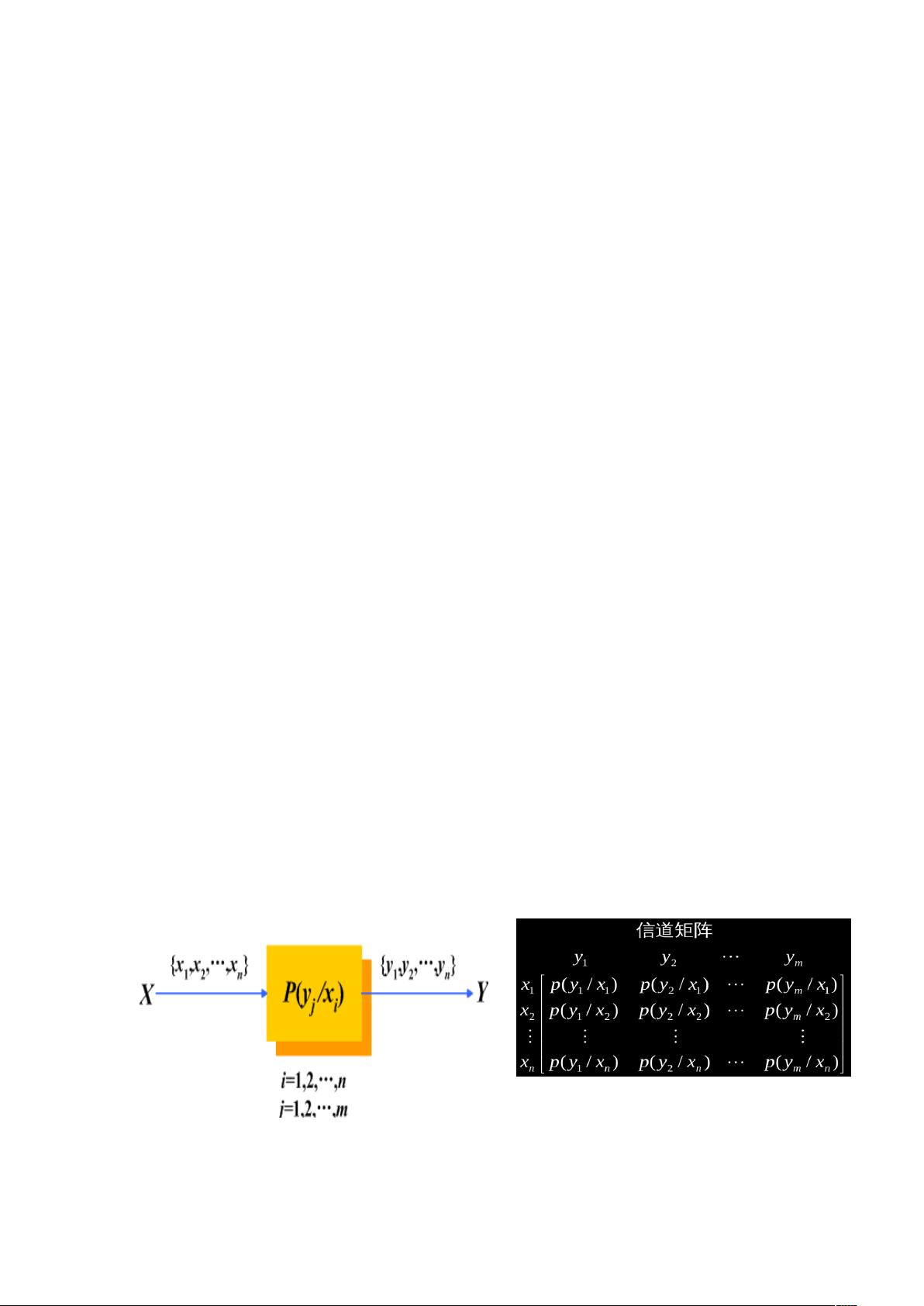
"信息论与信源编码实验" 本实验是针对信息论与信源编码领域的一个实践教学环节，旨在让学生深入理解和掌握信息量、信道容量、香农编码、费诺编码以及哈夫曼编码的基本概念和计算方法。通过计算机编程（C++语言）实现这些编码方式，学生将能够实际操作并分析编码效果。 实验一聚焦于信息量及信道容量的计算。信息量是衡量信息不确定性的度量，信源熵是描述信源输出不确定性的一个重要参数。实验要求学生计算离散无记忆信源的熵，同时考虑信道特性来计算信道容量。信道容量是指在保证一定误码率下，信道能传输的最大信息速率。实验过程中，学生需要熟悉信源熵、条件熵、联合熵、交互熵和信道容量的计算公式，并利用计算机程序进行模拟。 实验二介绍了香农编码，这是一种基于符号概率分布的前向编码方法。实验中，学生需要按照概率从大到小排序信源符号，计算自信息量，然后确定码字长度，最后将码字用二进制表示。香农编码确保了平均码长等于信源熵，从而达到最优编码效率。 实验三涉及费诺编码，这是一种构造固定码长的编码方式。实验要求学生根据信源概率分布将符号分组，使得各组概率和尽可能接近，然后为每个组分配唯一的码元。通过多级分组和编码，费诺编码可以实现接近信源熵的平均码长。 实验四则关注哈夫曼编码，这是一种自适应的前缀编码方法。哈夫曼编码通过构建哈夫曼树，将频率高的符号赋予较短的码字，频率低的符号赋予较长的码字。实验中，学生需要根据概率构建哈夫曼树，并生成相应的编码。 在每个实验中，学生都需要绘制程序流程图，编写程序代码，并记录调试过程中的问题。实验报告要求对结果进行分析，这有助于学生理解不同编码方法的优缺点，以及它们如何影响信息传输的效率和可靠性。 这些实验为学生提供了理论与实践相结合的学习机会，使他们能够运用信息论的理论知识解决实际编码问题，为未来在通信、数据压缩和信息传输等领域的工作打下坚实基础。