图的数据结构与算法解析

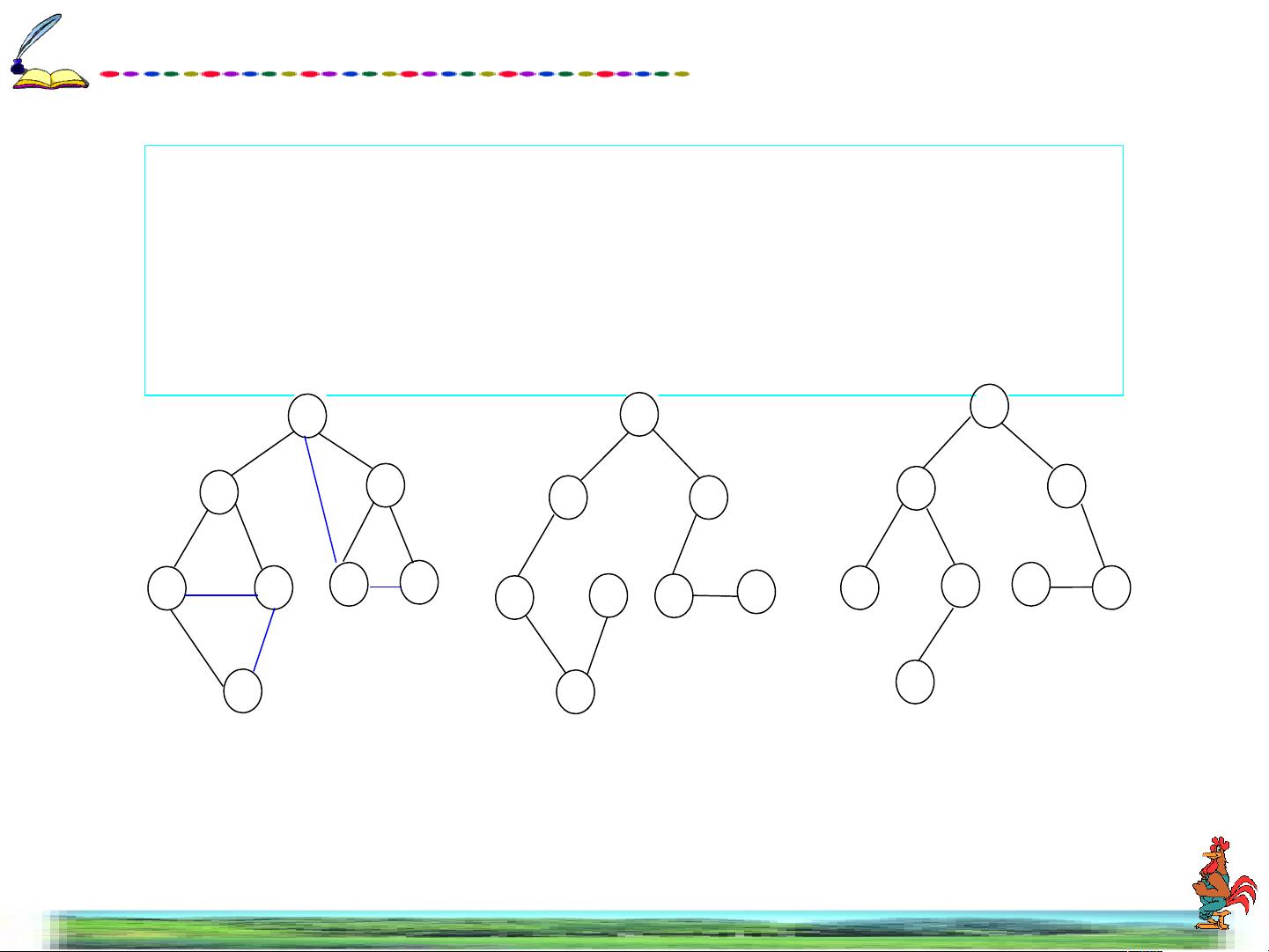
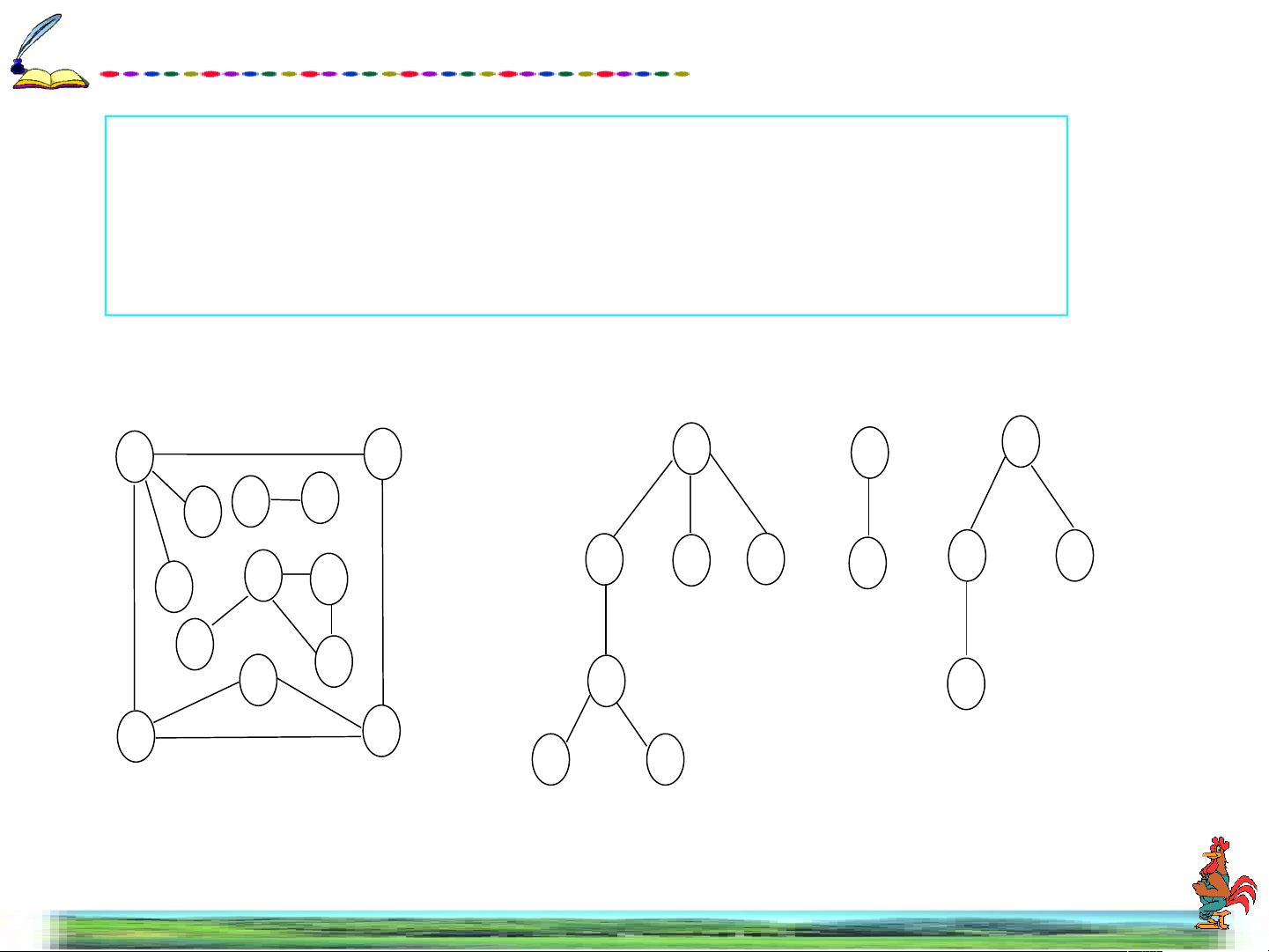
"数据结构-C语言版：DS07-图.ppt" 本文将深入探讨图这一重要的数据结构，它是计算机科学中处理复杂关系的基础。图由顶点（或节点）及其之间的关系（边）构成，可以用于表示各种实体间的联系，如网络中的设备连接、社交网络中的朋友关系等。 在图的定义中，一个图G=(V,E)，其中V是顶点的集合，E是边的集合。顶点通常代表数据对象，而边则表示它们之间的关系。图可以是有向的或无向的。有向图的边具有方向，即每条边从一个顶点指向另一个顶点，称为弧；无向图的边没有方向，任何两个顶点间可以互相连接。 完全图是一种特殊的图类型，无论是在无向还是有向情况下，任意两个顶点之间都存在边。对于无向完全图，边的数量为n(n-1)/2，而对于有向完全图，边的数量为n(n-1)。例如，一个有3个顶点的无向完全图将有3条边，而一个有3个顶点的有向完全图将有6条边，因为每对顶点之间都有两条方向相反的边。 在图的遍历中，我们通常有两种方法：深度优先搜索（DFS）和广度优先搜索（BFS）。深度优先搜索通过递归地访问每个顶点的邻居来探索图，而广度优先搜索则按层次顺序逐层访问顶点。 生成树是图的一个子集，它包含了图的所有顶点，且这些顶点由边连接成一棵树的结构，没有环。生成树在解决许多问题时非常有用，如最小生成树（如Prim算法或Kruskal算法）和最大流问题。 最短路径问题寻找的是在图中两个顶点之间路径的最小权重，例如Dijkstra算法和Floyd-Warshall算法常用于解决这类问题。这在路由计算、交通网络优化等领域具有实际应用。 拓扑排序是针对有向无环图(DAG)的操作，它将顶点排成线性序列，使得对于图中的每条有向边 (u, v)，顶点u都在顶点v之前。Kahn算法和拓扑排序是图处理中的重要工具。 总结来说，图数据结构在计算机科学中扮演着核心角色，它的理解和应用对于解决问题至关重要，特别是在网络分析、路径查找、算法设计等多个领域。掌握图的概念、存储结构、遍历方法以及生成树、最短路径和拓扑排序等操作，对于提升编程能力和解决实际问题的能力大有裨益。