"MATLAB实现可行方向法求极值问题"

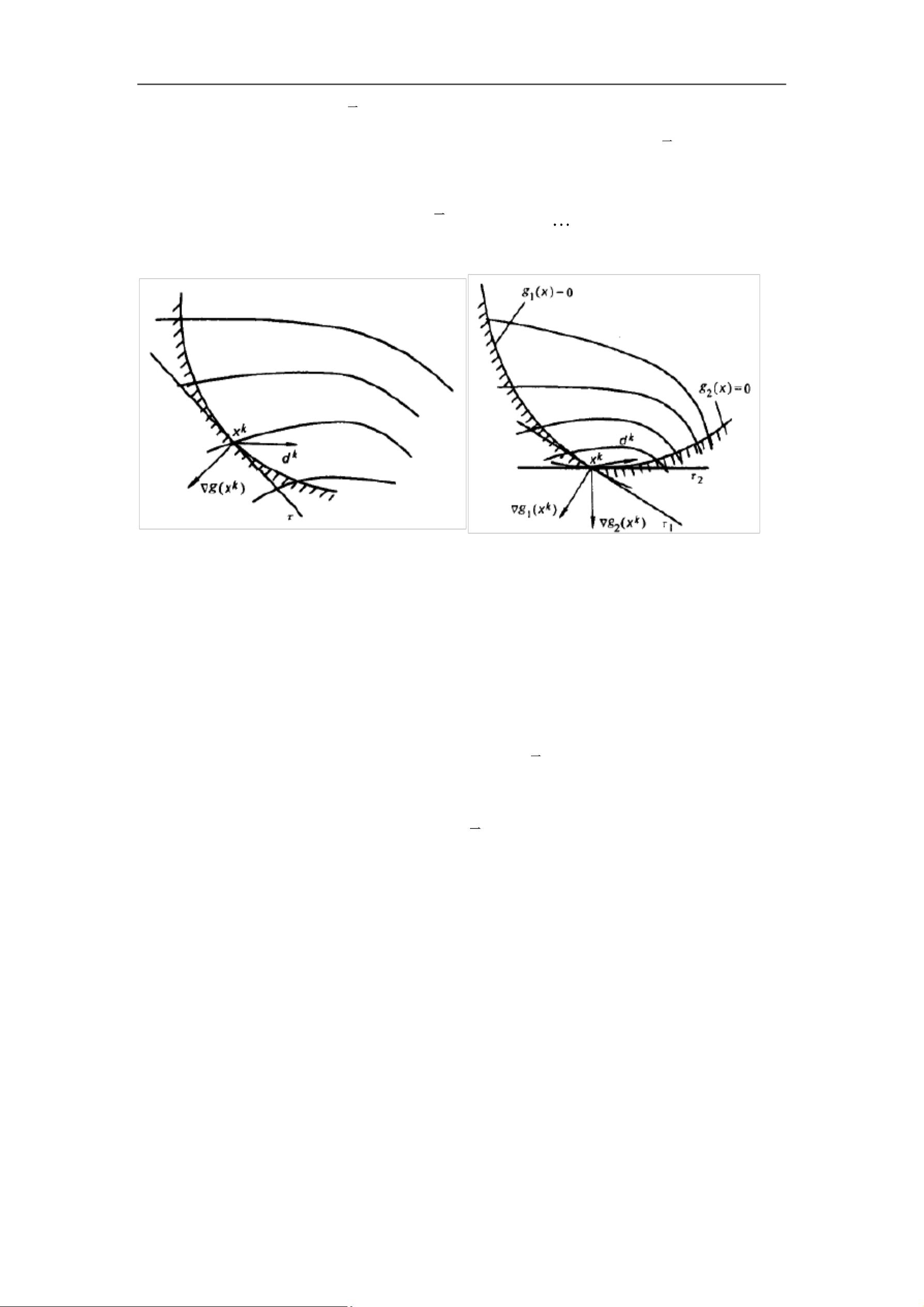
(k+1)仍为可行点，则停止迭代；否则，继续 2）由 X (k) 出发，沿可行方向移至某一个或 J 个起作用约束面的交集 X (k+1)，然后在交集上进行(Fletcher-Powell 1977)搜索； 3) 完全沿可行方向搜索，在可行域内继续移动以求得一个对 f (X) 的较大下降。可行方向法的搜索策略主要是在搜索时保持可行性，同时尽可能找到搜索到目标函数较小值的点。 1.2 可行方向法的数学描述 可行方向法的数学思想主要是在不断地沿着负梯度方向搜索，同时满足约束条件的情况下，逐步逼近极值点。首先，设优化问题为： 求 min f (X) s.t. g (X)  0 其中，f (X) 是目标函数，g (X) 是约束函数。 根据拉格朗日对偶性，可将原始的优化问题转化为如下的数学模型： 求 min f (X)  g (X) 其中， 是拉格朗日乘子。 可行方向法的基本思想是，先求得一个满足约束条件的初始点 X (0)，然后根据负梯度的方向和步长不断地更新当前点，直到满足终止条件为止。具体地，迭代的每一步可描述为： X (k+1)  X (k) kf (X (k)) 其中，f (X (k)) 是目标函数在点 X (k) 处的梯度；k 是在搜索方向上的步长。 在求解可行方向法的过程中，需要注意的是如何确定搜索方向和步长。通常可采用线性规划法确定搜索方向和约束最优步长法确定步长，详情将在后续章节中进行介绍。 2. MATLAB 中可行方向法的实现 在 MATLAB 中实现可行方向法求解极值问题可以分为以下几个步骤： （1）构建目标函数和约束条件函数。 （2）采用线性规划法确定搜索方向。 （3）采用约束最优步长法确定步长。 （4）根据步骤（2）和步骤（3）得到下一步的搜索点。 （5）判断终止条件是否满足，若满足则停止迭代，否则继续进行步骤（2）至步骤（4）直到满足终止条件。 3. 实例分析 为了验证可行方向法在 MATLAB 中的实现效果，我们选取了一个经典的优化问题作为算例进行分析。优化问题为： 求 min f (X)  (X1 1)2 (X2 1)2 s.t. g (X)  0 其中，g (X)  X1 X2 2（约束条件）。 利用 MATLAB 编写程序进行可行方向法求解，最终得到的最优解为 X opt = (1, 1)，f (X opt) = 0。从结果可以看出，可行方向法在 MATLAB 中的实现是正确并有效的。 4. 结论 本文介绶了可行方向法的基本数学思想和 MATLAB 中的实现方法，并通过算例验证了该方法的有效性。在工程实际的优化设计中，可行方向法作为一种有代表性的直接解法，能够快速高效地求解约束非线性问题，特别是对于大型约束优化问题具有一定的优势。因此，在实际工程中可行方向法有着广泛的应用前景。同时，通过本文的介绍和分析，读者可以更深入地了解可行方向法的原理和实现方法，在工程实践中能够更好地应用于优化设计中。