network of rectified linear units (ReLUs) given the concatenation of the previous latent layers as
input. This is analogous to the order-invariant encoding of set2set, but an output is produced at each
step, and processing is not gated [
65
]. The attentional mechanism is also effectively available to
property regressors that take the fixed-length latent representation as input, allowing them to aggregate
contributions from across the molecule. The output of the attentional mechanism is subject to batch
renormalization and a linear transformation to compute the conditional mean and log-variance of
the layer. The prior has a similar autoregressive structure, but uses neural networks of ReLUs in
place of Bahdanau-style attention, since it does not have access to the atom vectors. For molecular
optimization tasks, we usually scale up the term
KL [q(z|x)||p(z)]
in the ELBO by the number of
SMILES strings in the decoder, analogous to multiple single-SMILES VAEs in parallel; we leave this
KL term unscaled for property prediction.
GRU
1
GRU
2
h
T
1
h
T
2
Pool
Lin
z
1
Pool atoms
NN
Att
z
2
NN
Att
z
3
k
k
µ, σ
q
µ, σ
q
µ, σ
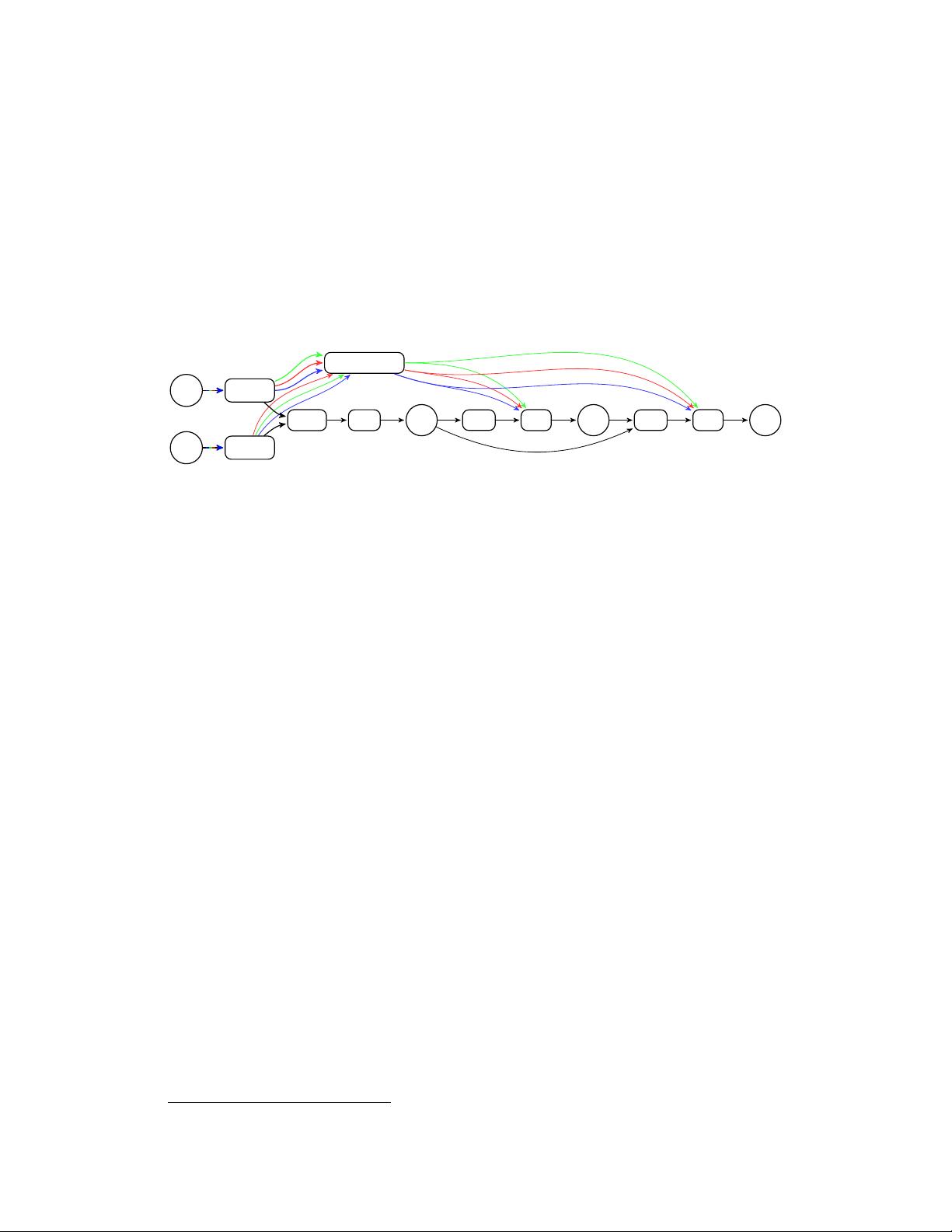
Figure 4: The approximating posterior is an autoregressive set of Gaussian distributions. The mean (
µ
)
and log-variance (
log σ
2
) of the first subset of latent variables
z
1
is a linear transformation of the
max-pooled final hidden state of GRUs fed the encoder outputs. Succeeding subsets
z
i
are produced
via Bahdanau-style attention with the pooled atom outputs of the GRUs as keys (
k
), and the query (
q
)
computed by a neural network on z
<i
.
The decoder is a single-layer LSTM, for which the initial cell state is computed from the latent repre-
sentation by a neural network, and a linear transformation of the latent representation is concatenated
onto each input. It is trained with teacher forcing to reconstruct a set of SMILES strings disjoint from
those provided to the encoder, but representing the same molecule. Grammatical constraints [
9
,
35
]
can naturally be enforced within this LSTM by parsing the unfolding character sequence with a
pushdown automaton, and constraining the final softmax of the LSTM output at each time step to
grammatically valid symbols. This is detailed in Appendix D, although we leave the exploration of
this technique to future work.
Since the SMILES inputs to the encoder are different from the targets of the decoder, the decoder
is effectively trained to assign equal probability to all SMILES strings of the encoded molecule.
The latent representation must capture the molecule as a whole, rather than any particular SMILES
input to the encoder. To accommodate this intentionally difficult reconstruction task, facilitate the
construction of a bijection between latent space and molecules, and following prior work [
28
,
67
], we
use a width-5 beam search decoder to map from the latent representation to the space of molecules at
test-time. Further architectural details are presented in Appendix B.
3.1 Latent space optimization
Unlike many models that apply a sparse Gaussian process to fixed latent representations to predict
molecular properties [
9
,
27
,
35
,
56
], the All SMILES VAE jointly trains property regressors with
the generative model [
42
].
2
We use linear regressors for the log octanol-water partition coefficient
(logP) and molecular weight (MW), which have unbounded values; and logistic regressors for the
quantitative estimate of drug-likeness (QED) [
4
] and twelve binary measures of toxicity [
22
,
45
],
which take values in
[0, 1]
. We then perform gradient-based optimization of the property of interest
with respect to the latent space, and decode the result to produce an optimized molecule.
Naively, we might either optimize the predicted property without constraints on the latent space, or
find the maximum a posteriori (MAP) latent point for a conditional likelihood over the property that
assigns greater probability to more desirable values. However, the property regressors and decoder are
only accurate within the domain in which they have been trained: the region assigned high probability
2
Gómez-Bombarelli et al. [16] jointly train a regressor, but still optimize using a Gaussian process.
5
剩余22页未读，继续阅读
狼You
- 粉丝: 26
- 资源: 324
我的内容管理
展开
最新资源
- 李兴华Java基础教程：从入门到精通
- U盘与硬盘启动安装教程：从菜鸟到专家
- C++面试宝典：动态内存管理与继承解析
- C++ STL源码深度解析：专家级剖析与关键技术
- C/C++调用DOS命令实战指南
- 神经网络补偿的多传感器航迹融合技术
- GIS中的大地坐标系与椭球体解析
- 海思Hi3515 H.264编解码处理器用户手册
- Oracle基础练习题与解答
- 谷歌地球3D建筑筛选新流程详解
- CFO与CIO携手：数据管理与企业增值的战略
- Eclipse IDE基础教程：从入门到精通
- Shell脚本专家宝典：全面学习与资源指南
- Tomcat安装指南：附带JDK配置步骤
- NA3003A电子水准仪数据格式解析与转换研究
- 自动化专业英语词汇精华：必备术语集锦
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
