数值计算中的导数估计：有限差分法详解

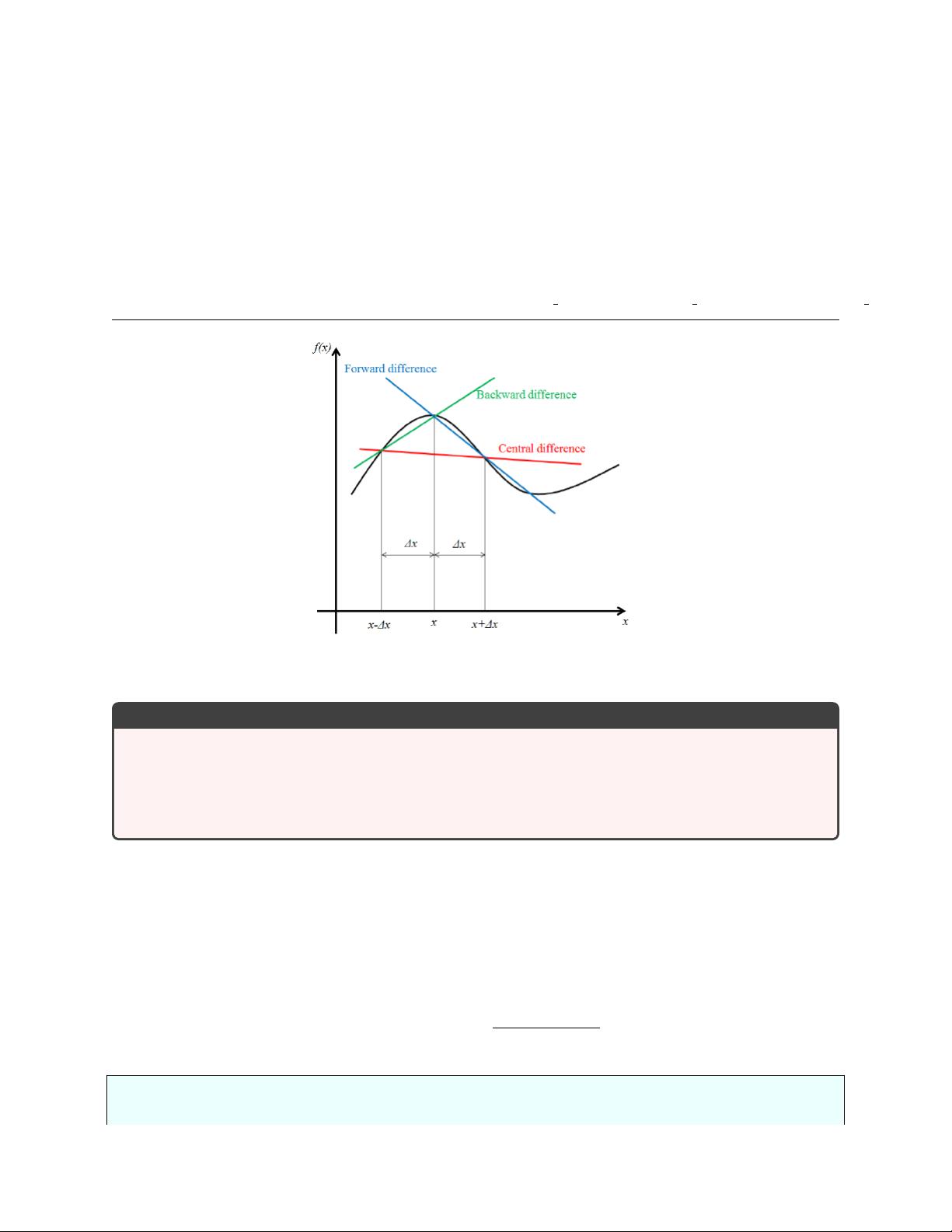
在IT行业的数值计算领域，特别是在科学计算中的数学方法课程MATH2070：数值方法I中，一个关键的主题是"Differentiation: The Finite Difference Method"。这个概念探讨了如何在没有解析微分工具的情况下估计函数的导数。当你需要计算函数f(x)的导数f'(x)，但缺乏解析表达式时，有限差分法是一个实用的数值技术。 核心的概念是使用有限差分，这是一种通过比较函数值在两个邻近点之间的变化来近似导数的方法。对于一个给定的函数值f(x)，如果想要估计f'(x)，可以采用前向差分法（forward difference），其基本思想是利用公式： \[ f'(x) \approx f_d(f, x, h) = \frac{f(x + h) - f(x)}{h} \] 这里，h表示差分步长或间隔，它直接影响估计的精度。较小的h通常会导致更精确的导数估计，因为误差会随着h的减小而减小。然而，这也带来了另一个挑战：随着h变小，计算次数增加，可能导致更大的浮点运算误差（round-off error）。 为了在MATLAB等编程环境中实现这一估计，可以编写一个函数，如所示： ```matlab function [fd] = forwardDifference(f, x, h) fd = (f(x + h) - f(x)) / h; end ``` 在这个函数中，输入函数f、参考点x以及步长h，函数返回相应的前向差分估计。实际应用中，需要谨慎选择h的值，以平衡精度和计算效率。同时，为了提高精度，可能还需要采用中心差分、复合差分等高级差分方法，或者使用数值稳定性的技巧来处理较大的h和浮点误差。 总结来说，有限差分方法是数值分析中一种基础且实用的工具，它在没有解析导数公式时提供了一种估计函数导数的有效途径。理解并掌握这一方法有助于在实际的科学计算和工程问题中进行准确的数值求解。