山东大学算法导论图论考试精华复习笔记

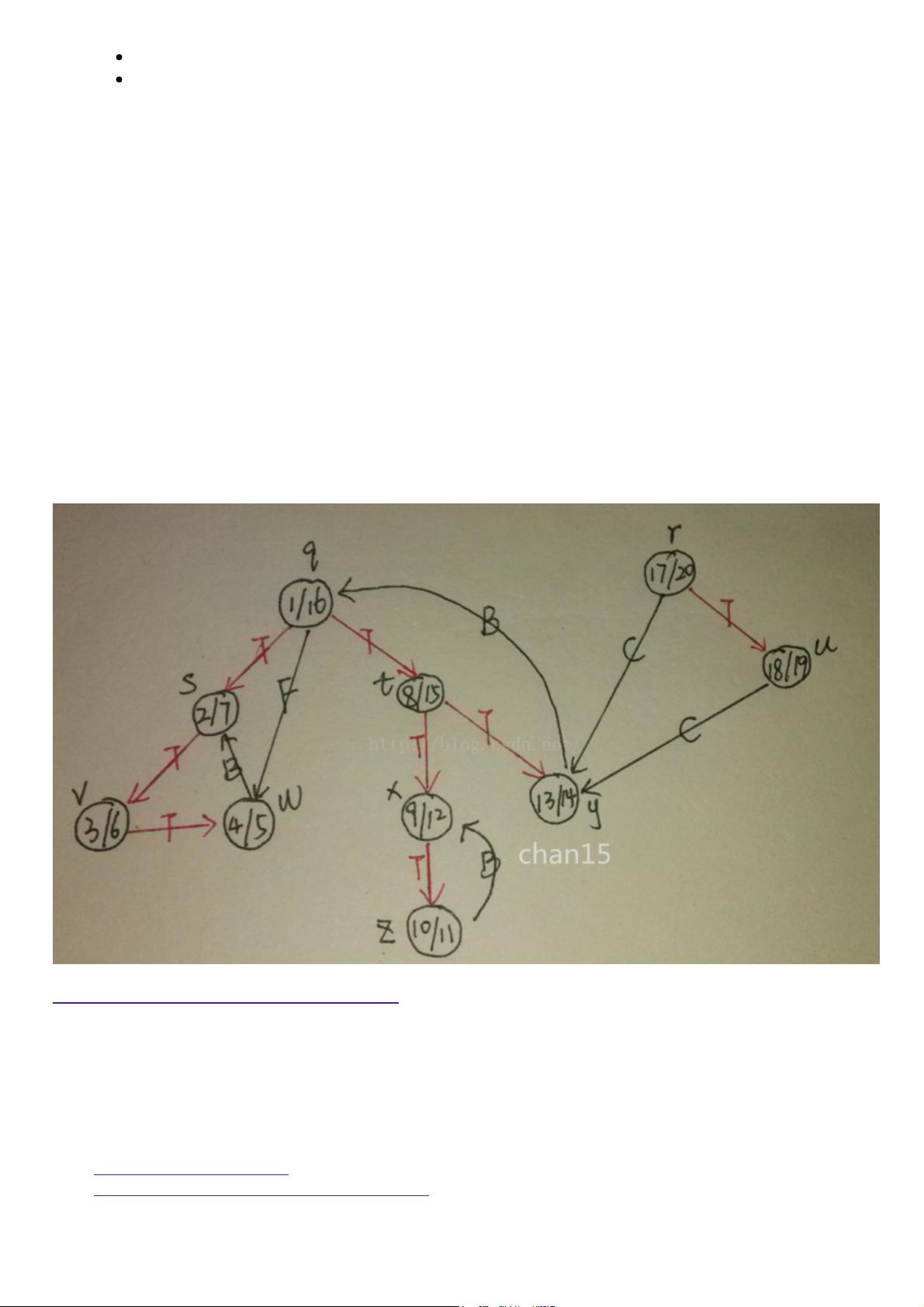
"这篇复习总结主要涵盖了山东大学2018年算法导论课程中关于图论的部分，包括图的基本算法、最小生成树、单源最短路径、所有节点对的最短路径问题以及最大流等核心概念和算法。这份资料详细介绍了各种算法的原理、实现方法以及相关性质，适合备考复习使用。" 在图论这个领域，图是数据结构中的重要组成部分，用于表示对象之间的关系。复习总结中提到了以下知识点： 1. **基本的图算法**： - **图的表示**：分为邻接链表（适用于稀疏图，即边的数量远小于顶点数量的平方）和邻接矩阵（适用于稠密图，即边的数量接近顶点数量的平方）。 - **BFS（广度优先搜索）**：基于队列的数据结构，时间复杂度为O(V+E)，其中V是顶点数量，E是边的数量。 - **DFS（深度优先搜索）**：可以递归实现或用栈，时间复杂度同样为O(V+E)，在搜索过程中会确定顶点的发现时间（d）和完成时间（f）。 2. **最小生成树**： - **最小生成树的形成**：连接图中所有顶点的边，使得树的总权重最小。 - **Kruskal算法**：按照边的权重从小到大选择边，避免形成环路。 - **Prim算法**：从一个顶点开始，每次添加一条连接当前树中顶点与树外顶点的最小权重边。 3. **单源最短路径**： - **Bellman-Ford算法**：适用于有权重的负边，可以检测负权环。 - **DAG图中的单源最短路径**：可以利用拓扑排序直接求解。 - **Dijkstra算法**：用于无负权边的图，采用贪心策略，找到源点到其他所有点的最短路径。 - **差分约束和最短路径**：在满足一定约束条件下，寻找满足条件的最短路径。 - **最短路径的性质证明**：如“三上无路收钱”是指不存在三条独立路径使得中间节点的费用比走两条路径的费用之和还要低。 4. **所有节点对的最短路径问题**： - **矩阵乘法**：在解决所有节点对最短路径时，可以考虑用矩阵快速幂算法进行优化。 - **Floyd-Warshall算法**：通过动态规划方法，逐步计算所有顶点之间的最短路径。 - **Johnson算法**：适用于稀疏图，通过调整权重来解决所有节点对的最短路径问题。 5. **最大流**： - **流网络**：包含容量限制和方向的图，目标是找到最大的流量从源点到汇点。 - **Ford-Fulkerson方法**：通过增广路径不断寻找并增加流，直到无法再增加为止。 - **最大二分匹配**：在二分图中找到最大数量的匹配边，是最大流问题的一个特例。 此外，复习资料还包括习题和附录中的运行时间表，对于深入理解和应用这些算法提供了实践基础。这份总结覆盖了图论中关键的算法和概念，对于学习和复习图论部分的知识非常有帮助。