微分方程基础：定义与几何解释

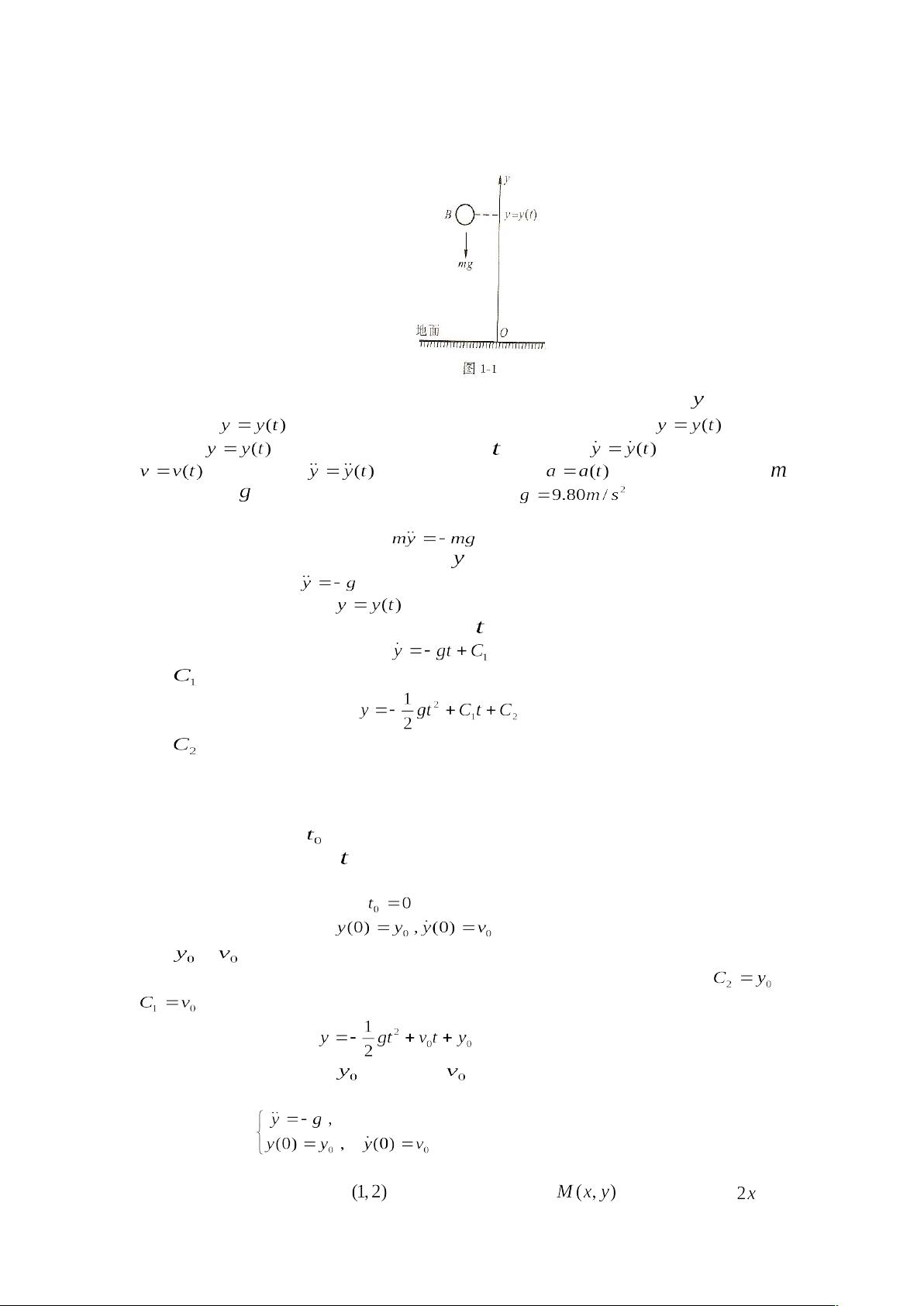
"常微分方程课件1/3 - 数学基础讲义" 常微分方程是数学的一个核心领域，它在自然科学、工程、经济学以及其他许多学科中都有着广泛的应用。这门学科关注的是通过解析或数值方法求解描述动态系统行为的微分方程。在本讲义中，我们将深入探讨常微分方程的基础理论和方法。 微分方程是用于描述物理、生物或其他系统动态变化的数学工具。例如，人口增长模型、生态系统中物种数量的变化、机械系统中的物体运动等都可以通过微分方程来建模。在这些模型中，未知函数代表系统的状态变量，其导数则表示这些状态变量的变化率。 第一章“基本概念”首先介绍了微分方程的定义。微分方程是一个包含了自变量、未知函数及其导数的方程。这里的自变量通常是时间，未知函数则是要找的解决方案，导数则反映了未知函数的变化率。例如，牛顿第二定律F=ma可以导出一个二阶常微分方程，用来描述质点在力的作用下的运动轨迹，其中未知函数代表质点的位置，一阶导数表示速度，二阶导数表示加速度。 定义1.1中指出，常微分方程是指涉及自变量、未知函数及其最高至n阶导数的方程，n即为该方程的阶数。方程中的已知函数通常与问题的具体情境有关，例如物理定律。值得注意的是，只有当方程中包含未知函数及其导数时，它才被称作常微分方程，不含导数的方程则不属于这一类别。 在后续章节中，我们将学习如何求解这些微分方程，包括初值问题和边值问题，以及解的性质，如存在性、唯一性和稳定性。此外，还会讨论线性微分方程、非线性微分方程、常系数微分方程和变系数微分方程等特殊类型，以及数值解法，如欧拉方法和龙格-库塔方法。 常微分方程的理论和方法不仅限于理论研究，它们在实际应用中同样重要。通过求解微分方程，我们可以预测系统的行为，设计控制系统，或者理解复杂现象背后的动态机制。因此，掌握常微分方程的理论和技能对于任何想要深入探索科学和技术领域的学者来说都是必不可少的。