概率理论驱动的H.264到H.265转码视频客观质量评估新法

需积分: 5 18 浏览量更新于2024-08-26 收藏 1.1MB PDF 举报

本文主要探讨了"基于概率理论的从H.264 / AVC到H.265 / HEVC转码视频的客观质量评估方法"。H.265 / HEVC作为继H.264 / AVC之后的最新视频编码标准，旨在提供更高的压缩效率和更好的图像质量。然而，由于大量的现有内容是采用H.264 / AVC编码的，为了兼容性和升级需求，视频转码从H.264 / AVC到H.265 / HEVC成为必要。传统的转码过程中，虽然可以容易地计算出转换后的视频相对于原始H.264 / AVC解码视频的失真度，但实际的原始视频往往不可用，这就导致了难以精确衡量转码视频与原始视频之间的质量差异。这一问题对于确保转码后视频的质量控制至关重要，尤其是在追求高质量的播放体验时。作者Xiwu Shang、Haiwu Zhao、Guozhong Wang、Xiaoli Zhao和Yifan Zuo针对这一挑战，提出了一个新颖且准确的转码视频质量评估方法。他们利用概率论原理，设计了一种能够预测转码视频客观质量的方法。这种方法通过数学建模和统计分析，试图捕捉视频编码过程中可能的不确定性，并以此来估计转码后视频的质量接近度。实验结果显示，该方法预测的转码视频质量与实际质量有良好的一致性，表明其在实际应用中的有效性。这对于视频服务提供商来说，是一个重要的改进，因为他们可以利用这个工具来优化转码过程，确保在提升编码效率的同时，保持或接近于原始视频的质量水平，从而提高用户满意度。这篇研究论文为视频转码领域的质量评估提供了一个创新的解决方案，有助于解决传统方法在评估H.264 / AVC到H.265 / HEVC转码质量时面临的难题。随着H.265 / HEVC的广泛应用，这项工作对于推动视频编码技术的发展以及优化多媒体内容的传输和处理具有重要意义。

IEEE TRANSACTIONS ON BROADCASTING, VOL. 65, NO. 4, DECEMBER 2019 777

A Novel Objective Quality Assessment Method for Transcoded Videos

From H.264/AVC to H.265/HEVC Utilizing Probability Theory

Xiwu Shang , Haiwu Zhao, Guozhong Wang, Xiaoli Zhao, and Yifan Zuo

Abstract—The latest video coding standard H.265/HEVC is developed

to succeed the previous coding standard H.264/AVC. However, a large

amount of legacy content was coded with H.246/AVC. Therefore,

transcoding from H.264/AVC to H.265/HEVC format is required. During

the process of transcoding, we can easily calculate the distortion of the

transcoded video with respect to the H.264/AVC-decoded video. However,

since the original video is usually unavailable, the distortion between the

original video and the transcoded video is unknown, which makes it dif-

ﬁcult to control the coding quality of the transcoded video compared to

the original video. In this paper, we propose a novel and accurate qual-

ity estimation method for transcoded videos utilizing probability theory.

Experimental results demonstrate that the predicted quality of transcoded

videos approximate the true value, with an average error of 0.28 dB,

0.41 dB, and 0.46 dB for Y, Cb, and Cr components, respectively.

Index Terms—

Video quality assessment, PSNR, probability

theory.

I. I

NTRODUCTION

HE H.264/AVC standard [1] has been a widely used video

coding standard in practical application such as online video

streaming, broadcast over satellite, applications over cable or wire-

less networks. However, with the popularity of high deﬁnition (HD)

or even ultra high deﬁnition (UHD), a more efﬁcient video coding

standard is urgently required. Therefore, in 2010, the joint collabora-

tive team on video coding (JCT-VC) was established to develop the

next coding standard. In January 2013, the high efﬁciency video cod-

ing standard H.265/HEVC was formally ﬁnalized roughly doubling

the compression performance compared with H.264/AVC [1], [2].

Therefore, it is expected that H.265/HEVC will gradually replace

H.264/AVC in the near future. Considering the existence of numerous

H.264/AVC-coded legacy contents and the high coding performance

of H.265/HEVC, a transcoder [3], [4] which can convert H.264/AVC

bitstreams into H.265/HEVC bitstreams is required in many applica-

tions.

Generally, transcoders can convert one compressed video for-

mat into another one, which includes encoding syntax, frame rate,

bitrate, and spatial resolution [4]. In this paper, we focus on the

research of the transcoder converting from H.264/AVC bitstream into

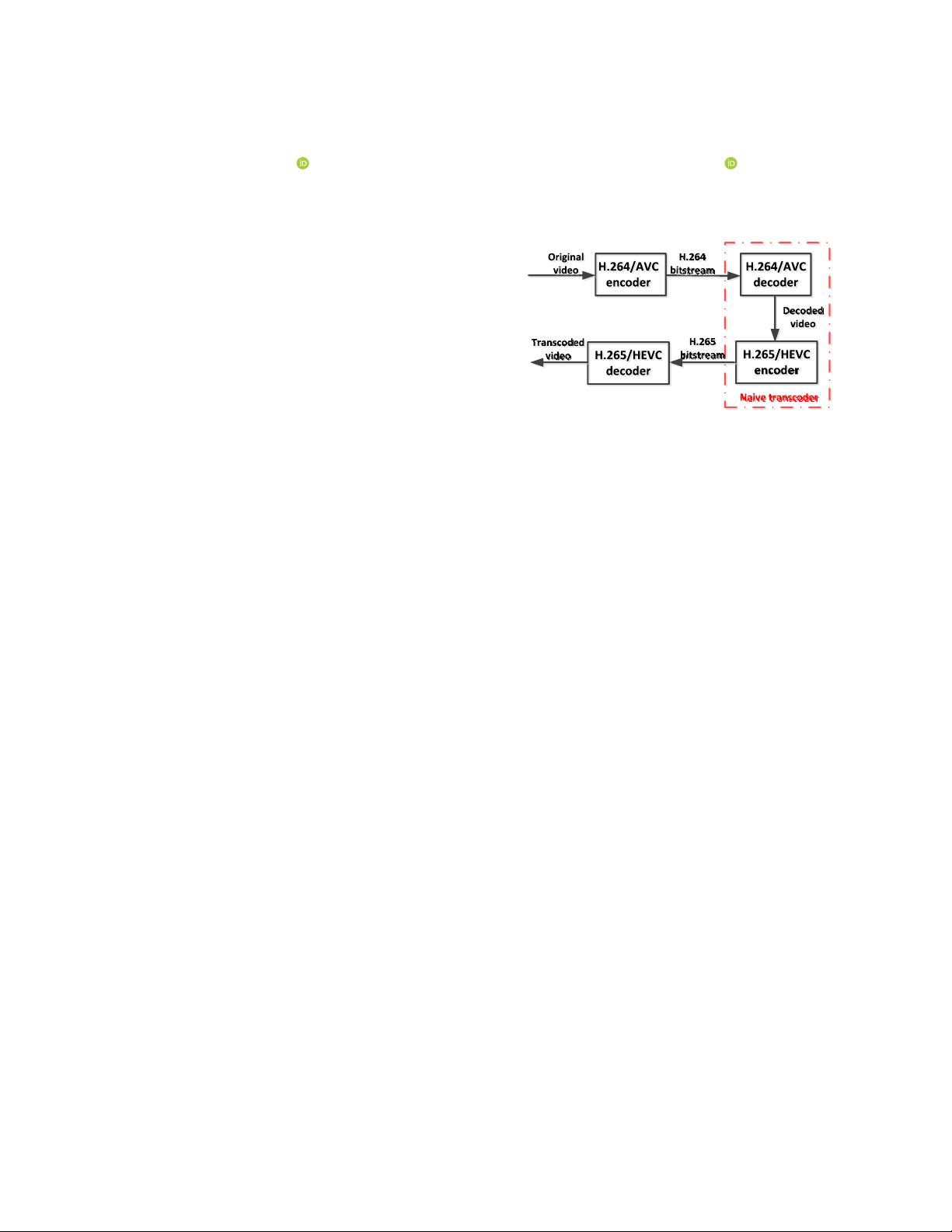
H.265/HEVC bitstream. A naive transcoder in the dashed box is

shown in Fig. 1, which is composed of a decoder and a cascaded

Manuscript received April 2, 2019; revised June 28, 2019; accepted July

29, 2019. Date of publication August 20, 2019; date of current version

December 10, 2019. This work was supported in part by the National

Science Foundation of China under Grant 61601296, and in part by the

Start-Up Research Project of SUES under Grant 0232-E3-0507-19-05106.

(Corresponding author: Guozhong Wang.)

X. Shang, G. Wang, and X. Zhao are with the School of Electronic

and Electrical Engineering, Shanghai University of Engineering Science,

Shanghai 201620, China (e-mail: dxsxw@126.com; wanggz@sues.edu.cn;

evawhy@163.com).

H. Zhao is with the School of Communication and Information

Engineering, Shanghai University, Shanghai 200444, China (e-mail:

zhaohaiwu@i.shu.edu.cn).

Y. Zuo is with the School of Information Technology, Jiangxi

University of Finance and Economics, Nanchang 330013, China (e-mail:

kenny0410@sina.com).

Color versions of one or more of the ﬁgures in this article are available

online at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/TBC.2019.2932286

Fig. 1. The process of transcoding.

encoder. The input bitstream is decoded by H.264/AVC decoder ﬁrst.

Then by H.265/HEVC encoder, the reconstructed video is coded into

H.265/HEVC bitstream. To provide a satisfactory video quality for

the transcoded video, models of video quality assessment are required

to monitor the quality of service (QoS).

Traditional video quality assessment schemes are classiﬁed into

three categories based on the availability of the original videos: full-

reference (FR) schemes, reduced-reference (RR) schemes, and no-

reference schemes (NR).

FR schemes assume that the original video is available by which

the impared video quality is measured. The peak signal to noise ratio

(PSNR) and structure similarity (SSIM) [5], [6] are examples of such

schemes. PSNR and SSIM only measure the distortion of one chan-

nel instead of the distortion of the three channels (YCbCr). In our

previous works [7], [8], we provide a color-sensitivity-based com-

bined PSNR (CSPSNR) method based on the sensitivity of the three

channels to measure the quality of the entire sequence.

RR scheme evaluates the video quality by referencing part of the

original data. In [9], a RR quality assessment algorithm is proposed

by reorganizing DCT coefﬁcients into three subbands, each of which

is modeled as generalized Gaussian density (GGD). The parameters

of the GGD of the original picture are sent to the decoder side to

analyze the distortion. Wang et al. [10] assume that the image qual-

ity is closely related to the amount of uncertainy [11] and primary

visual information [12] according to the internal generative mech-

anism (IGM). Then they develop a RR method for screen content

image by comparing the similarities of the two components.

NR schemes measure the quality blindly without using the original

videos, which is more practical in real application for the undis-

torted reference signal is always unavailable. Currently, several blind

video quality assessment algorithms are proposed. Mittal et al. [13]

proposed an algorithm of Blind/Referenceless Image Spatial QUality

Evaluator (BRISQUE) in spatial domain, which focuses on ana-

lyzing the statistical characteristics of locally normalized lumi-

nance coefﬁcients to quantify the distortion of natural images.

Shim et al. [14] estimate the PSNR value at the decoder side of

H.264/AVC by approximating the distribution of DCT coefﬁcients

as Cauthy distribution. To calculate PSNR is equivalent to calcu-

late the Mean Squared Error (MSE). Then the MSE in the spatial

domain is calculated in the transform domain according to Parseval’s

Theorem. Methods [15]–[18] are all developed in a similar way. The

previous methods focus on estimating the PSNR due to quantization

0018-9316

 2019 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.

See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

下载后可阅读完整内容，剩余4页未读，立即下载

weixin_38615591

粉丝: 5
资源: 977

概率理论驱动的H.264到H.265转码视频客观质量评估新法

H.265/HEVC：超越H.264/AVC的高清视频编码技术解析

H.264/AVC到HEVC高效转码：基于预测同质性的优化策略

H.264/AVC：视频编码标准概述与技术特性

基于Fisher判别分析的H.264 / AVC到HEVC转码的快速CU分区

H.264/AVC、H.265/HEVC、VP8、VP9、AV1的对比

Effective H.264/AVC to HEVC Transcoder based on Prediction Homogeneity

ITU-T-H.264.rar_H.264 解码_H.264/AVC_h 264 document_itu_itu-t h.2

H.264/avc经典教程

H.264/AVC视频编码标准详解

H.264/AVC视频编码标准概览

最新资源