高真实感流体模拟：基于SPH的多分辨率可视化方法

180 浏览量更新于2024-08-28 收藏 1.28MB PDF 举报

本文档探讨了流体模拟的可视化技术，特别是基于 smoothed particle hydrodynamics (SPH) 的多分辨率方法。SPH是一种在计算流体力学中广泛使用的数值模拟技术，它通过将连续介质分解为大量粒子来模拟流体行为，每个粒子代表一个体积元素，通过邻近粒子之间的相互作用来模拟流体动力学效应。文章首先强调了流体模拟在虚拟训练、教育、计算机游戏以及数字娱乐等领域的重要性，这些应用领域对视觉真实感有极高的需求。作者关注的问题是如何生成具有高度视觉逼真的流体模拟结果，这对于提升用户体验和沉浸式效果至关重要。针对这一挑战，研究者提出了一个基于SPH的多分辨率方法。这种方法的核心在于利用不同分辨率级别来处理流体模拟的不同部分。高分辨率区域用于模拟细节丰富的区域，如涡旋或喷射，而低分辨率区域则处理大规模的流动或背景环境，这样可以节省计算资源并提高效率。通过这种方式，研究人员能够平衡视觉质量与计算复杂度之间的关系。文中可能详细讨论了如何设计和实现这种多分辨率策略，包括粒子的细化和合并策略，以及如何在不同分辨率下保持物理一致性。此外，他们可能会探讨如何结合并行计算技术来加速处理大规模的SPH模拟，因为这在实际应用中是必不可少的。资金支持方面，该研究得到了中国国家自然科学基金（Nos. 61572299, 61402270, and 61472232）和山东省重点研发计划（Grant/AwardNumber: 2017GSF20105）的资助，显示出研究团队对于高性能流体模拟技术研发的重视和投入。这篇文章深入研究了如何通过SPH技术优化流体模拟的可视化，提出了一种创新的多分辨率方法，以满足日益增长的高真实感流体模拟需求。这对于提高仿真系统的性能和用户体验具有显著的意义，也为其他研究者提供了在复杂场景下进行高效流体模拟的新思路和技术参考。

ZHANG ET AL. 3of14

2.3 Surface construction with particles

Extracting the fluid surface from particles is an essential step in the Lagrangian approach. However, such extraction is challenging owing to sev-

eral limitations, such as increased memory consumption and computational cost. Given a particle set, general methods often build a scalar field

and extract surface mesh from the scalar field using the marching cubes algorithm.

To alleviate the bumpiness of the constructed surface mesh,

Zhu and Bridson

compute the scalar field with a signed distance function and extract the zero iso-surface to represent the liquid surface.

Onderik et al

and Solenthaler et al

improve the method to reduce artifacts in a concave region of the liquid surface. In the work of Williams,

smooth surface construction is regarded as an optimization problem. However, the ignorance of temporal continuity yields oscillation during sim-

ulation. Bargteil et al

combine the level set method with the Laplacian operation to smooth out the surface. The smoothing step may filter out

high-resolution details. Yu and Turk

obtain smooth fluid surface using anisotropic kernel function, which is costly in simulation. Akinci et al

17,32,33

execute surface extraction with two steps: surface decimation and surface subdivision; such extraction produces smooth surface with high effi-

ciency. However, expressing multi-resolution details computed from the adaptive SPH model is difficult. In addition, constructing highly accurate

fluid surface requires a smaller grid size and a larger influence radiusof each particle. As a result, the computational cost and memory consumption is

dramatically increased.

Considering the multi-scale features of the fluid surface, we use a multi-resolution method to construct the fluid surface. The method is inspired

by the surface construction methods

in multi-view stereo area. This method facilitates the processing of the particles with different radii and

non-uniform distribution in the adaptive SPH model. Our method can effectively produce fluid simulation with fine resolution details because of

combining fluid computation and fluid surface construction in a single framework.

3 METHODS

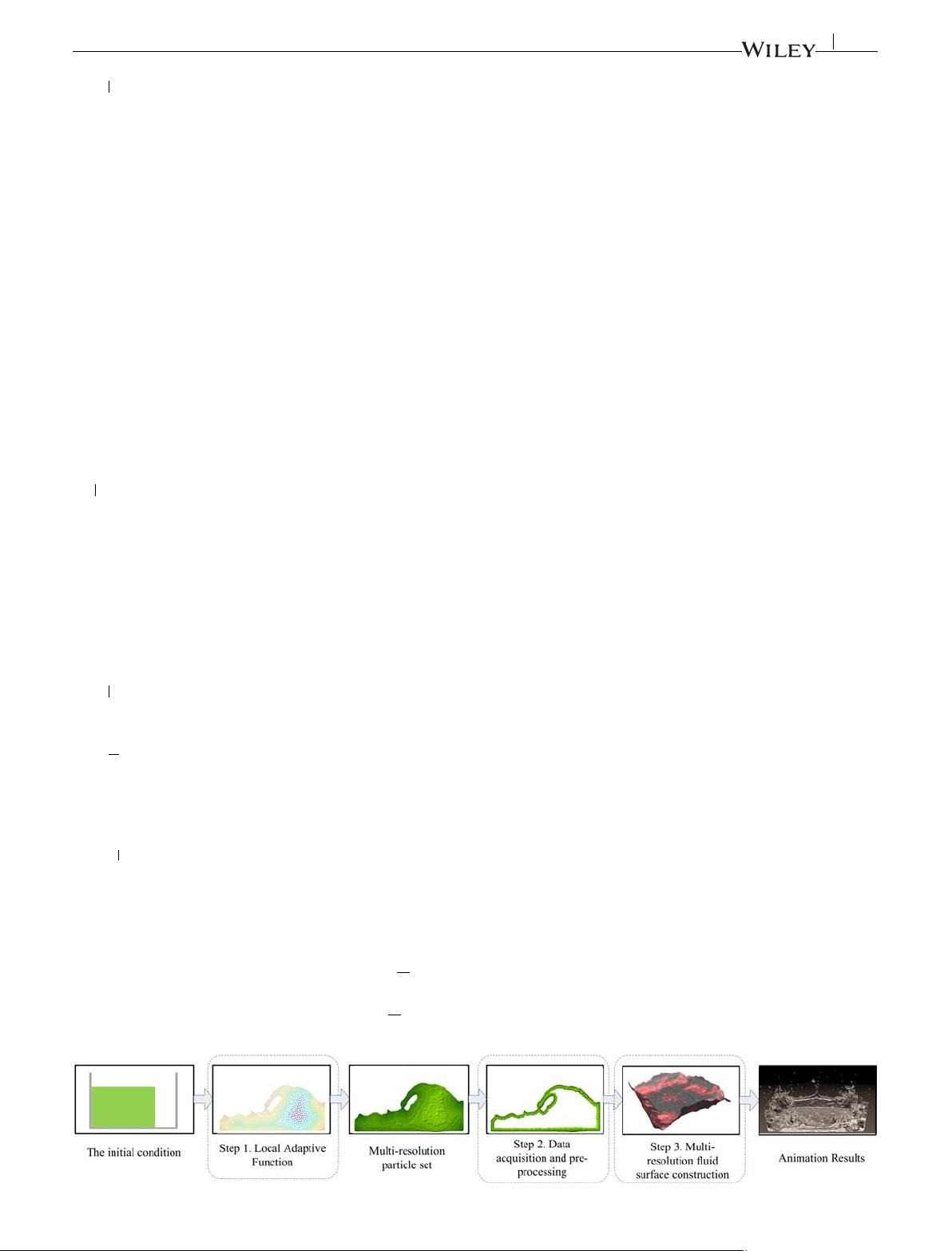
Figure 1 shows the framework of the proposed method. The method involves three main steps: multi-resolution local adaptive fluid computation,

data acquisition and pre-processing, and multi-resolution surface construction.In the first step, the physical fluid model is solved with our novel

adaptive SPH method given initial and boundary condition to obtain the multi-resolution particle set. In the second step, sample points are obtained

from the multi-resolution particle set, and the attributes (eg, footprint size and confidence value) of these sample points are computed. In the third

step, multi-resolution fluid surface is built iteratively by a graph cut algorithm on a weighted graph formulated from the global confidence map on a

crust of fluid computational domain. We employ the photo-realistic rendering algorithm

to obtain the fluid simulation results.

3.1 Local adaptive multi-resolution fluid computation model

Let P be the particle set of the SPH model. To express multi-resolution features, particles in P are initialized with different levels l = 0, 1, 2, … , where

a particle at level l = 0 has the smallest mass m and radius r. Then, the mass m

and radius r

of particle p

at level l can be written as m

= 2

m and



r. The average of the initial inter-particle spacing is set as r

∕h, where h is a control parameter and is set as h = 2.5 in our experiment. If the

distance between two particles p

and p

satisfies



− x



≤ max(r

, r

),thenp

and p

are neighbors. A k-dimensional (KD) tree is built to store the

particle set P, such that the neighbor particles can be queried efficiently.

3.1.1 Fluid computation based on SPH model

Let u

and x

be the velocity and position of the particle p

at time step n. Our goal is to compute u

n+1

and x

n+1

at the next time step n+1 by solving the

physically based fluid model.

(1) Particle-based fluid model

To compute particle velocity at time step n+1, the Naiver-Stokes equation must be solved first, as follows:

𝜕𝜌

𝜕t

+∇·

(

𝜌

)

= 0,

(1)

𝜌



𝜕

𝜕t

u ·(∇u)



=−∇p + 𝜌g + 𝜇∇

u, (2)

FIGURE 1 The framework of our method

剩余13页未读，继续阅读

weixin_38741030

粉丝: 3
资源: 924

高真实感流体模拟：基于SPH的多分辨率可视化方法

基于粒子的流体模拟：SPH技术与光线追踪渲染

GPU加速SPH流体模拟：实时与高效

开源流体算法库：基于粒子的粘弹性模拟

经典流体模拟—SPH源代码

SPH光滑粒子流体动力学 模拟代码

毕业设计-流体模拟.zip

IllustrisAnalysis:Illustris 模拟分析

unity流体效果插件--Obi Fluid

双尺度粒子模拟

有限元方法计算泥石流无网格方法

最新资源

SPH光滑粒子流体动力学模拟代码