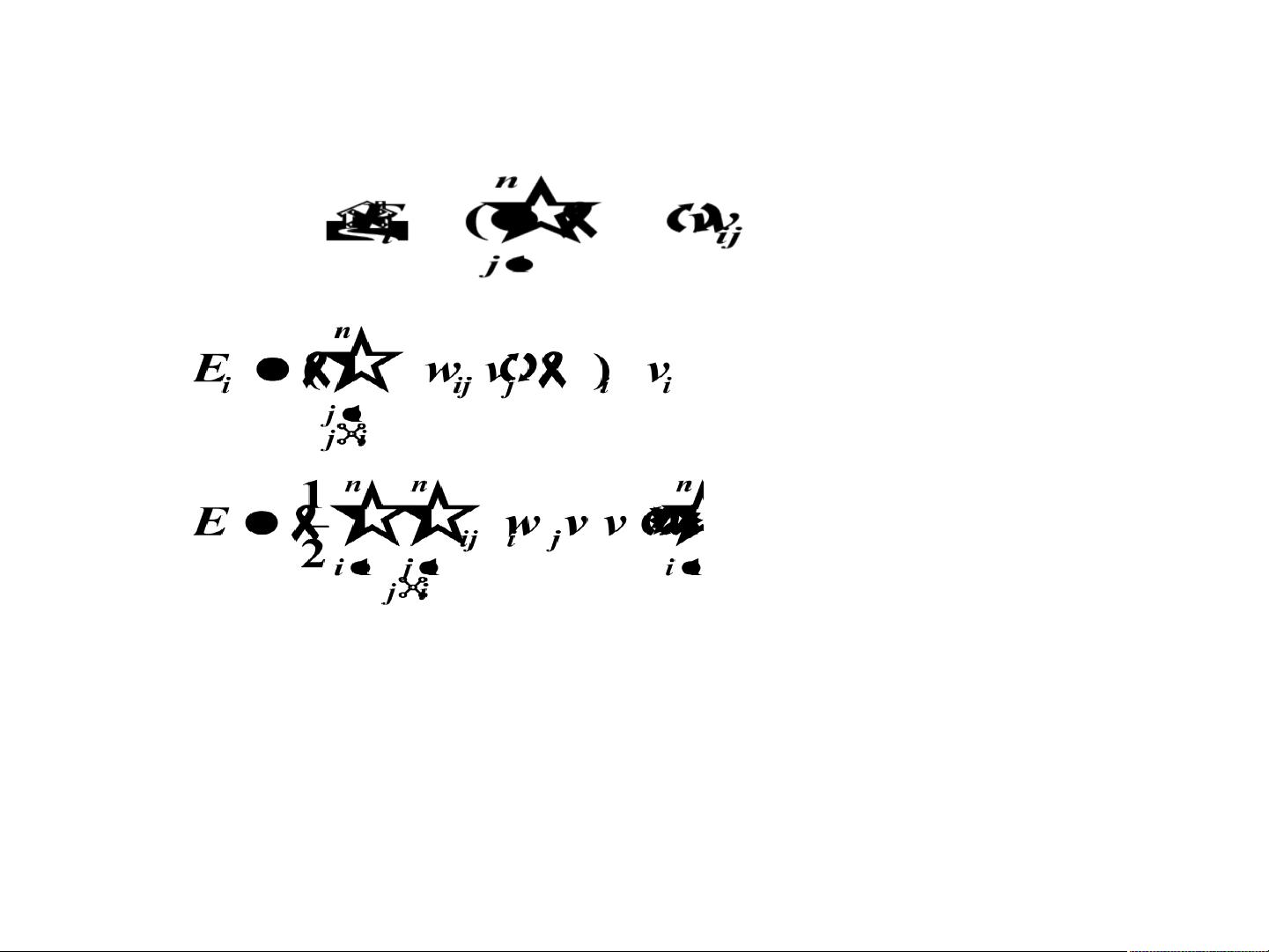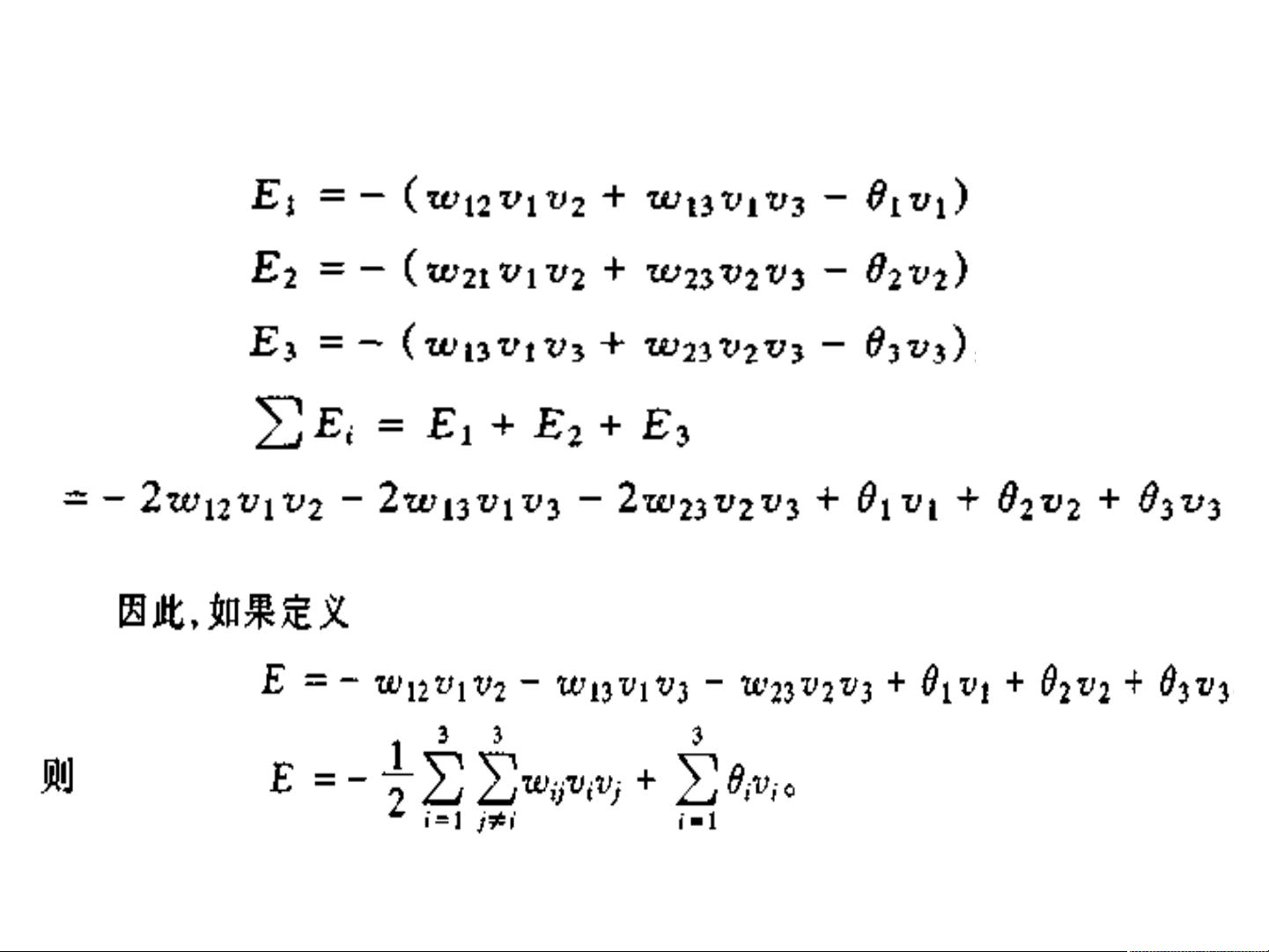霍普菲尔德神经网络：反馈型动力系统与应用

第10章人工神经网络-Hopfield.ppt主要介绍了霍普菲尔德神经网络（Hopfield Neural Network，HNN），这是一种由J.J. Hopfield和D.W. Tank在1985年提出的重要反馈型神经网络模型。与前向神经网络不同，Hopfield网络具有强大的计算能力和联想记忆功能，特别适用于解决诸如旅行商问题（TSP）的约束优化问题。 该模型的核心在于其反馈结构，这使得系统能够通过稳定状态的变迁实现学习记忆过程，其动力学特性决定了网络的稳定性。Hopfield网络的稳定性与其能量函数密切相关，能量函数的最小化是网络达到稳定状态的驱动力。网络的结构形式包括单层对称全反馈网络，分为离散型（DHNN）和连续型（CHNN）两种，分别依据不同的激励函数——δ函数用于联想记忆，S型函数用于优化计算。 网络的状态演变表现为非线性动力学系统的几种形式，包括渐进稳定（系统从任意初始状态最终趋于某个稳定状态）、极限环（系统在有限范围内周期性振荡）、混沌现象（系统行为表现出不可预测的复杂模式）以及状态轨迹发散（系统失去稳定，状态不再收敛）。符号函数激励的霍普菲尔德网络可以用如下的微分方程来描述其输入输出关系： \[ \frac{du_i}{dt} = -\frac{\partial E}{\partial u_i}, \quad i=1,2,\ldots,n \] 其中，\(E\) 是网络的能量函数，\(u_i\) 是神经元的输出，\(t\) 是时间，\(n\) 是神经元的数量。理解并掌握这些动力学特性对于Hopfield神经网络的设计和实际应用至关重要。 霍普菲尔德神经网络是一种具有深刻理论内涵和广泛应用前景的反馈型人工神经网络模型，它的研究不仅推动了非线性动力学系统的研究，也在模式识别、数据处理和机器学习等领域展示了其独特的价值。