二分算法深入解析:从二分查找至二分答案
需积分: 1 13 浏览量
更新于2024-06-16
收藏 3.21MB PDF 举报
“C语言-01-二分算法提高之二分答案.pdf”主要讲解了二分算法在C语言中的应用,特别是二分查找及其变种的应用。
二分算法是一种高效的数据搜索方法,其核心思想是利用有序序列的特性,通过每次将搜索范围减半来快速定位目标值。这种算法的时间复杂度为O(logn),相比线性搜索的O(n)有着显著的优势。但要注意,二分算法的前提是数据必须是有序的,无论是严格递增还是严格递减。
在二分查找的基本形式中,首先确定查找区间的上下界,然后计算中间位置的索引,通过比较中间元素和目标值的关系,将查找区间缩小至中间元素的一侧。这个过程不断重复,直到找到目标值或查找区间为空。基本的二分查找算法可以用循环或递归两种方式实现。代码示例如下:
```c
// 循环实现
int bs(int data[], int low, int high, int k) {
while (low <= high) {
int mid = (low + high) / 2;
if (k == data[mid])
return mid;
else if (k < data[mid])
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
// 递归实现
int bs(int data[], int low, int high, int k) {
if (low <= high) {
int mid = (low + high) / 2;
if (k == data[mid])
return mid;
else if (k < data[mid])
return bs(data, low, mid - 1, k);
else
return bs(data, mid + 1, high, k);
}
return -1;
}
```
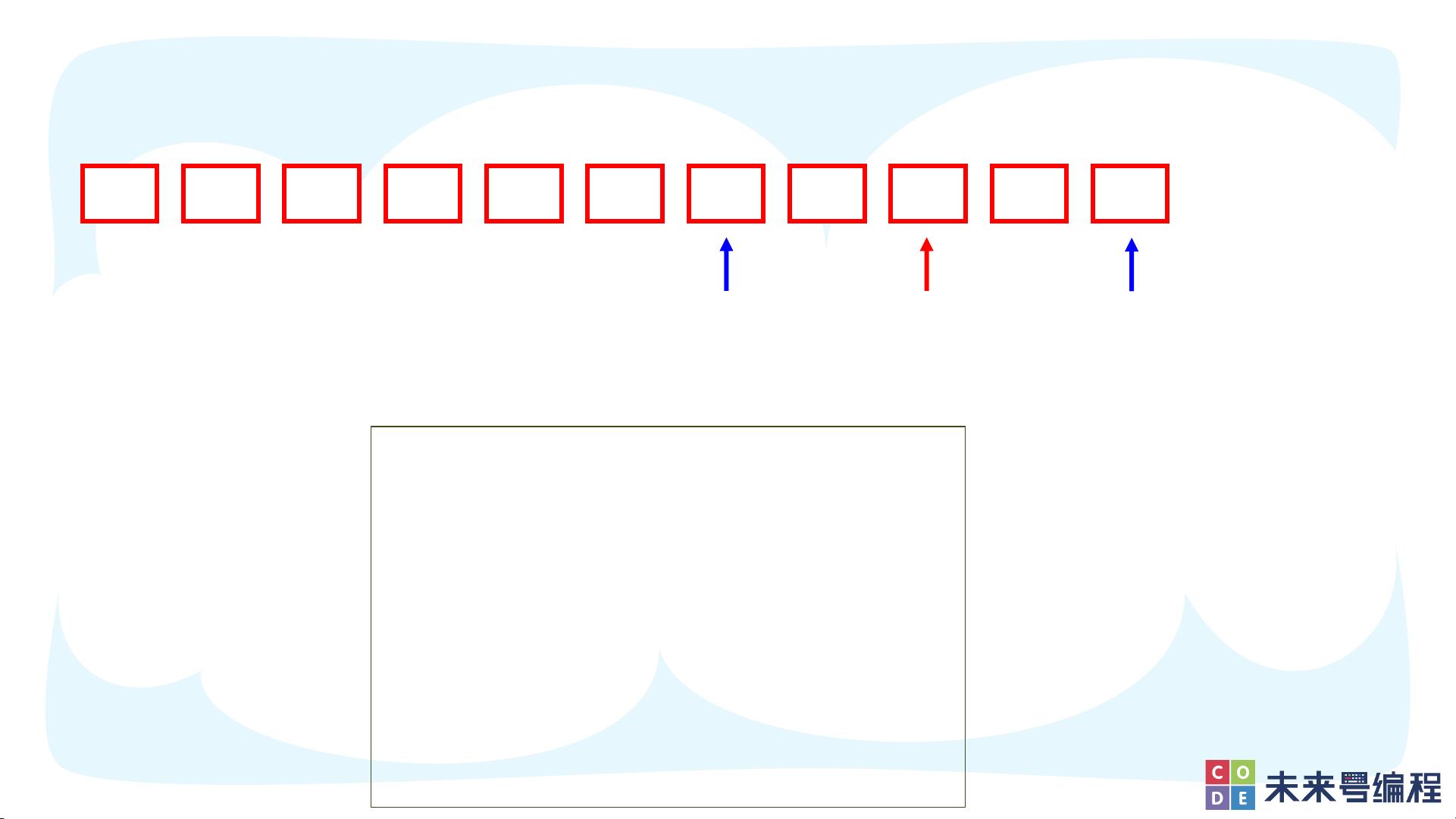
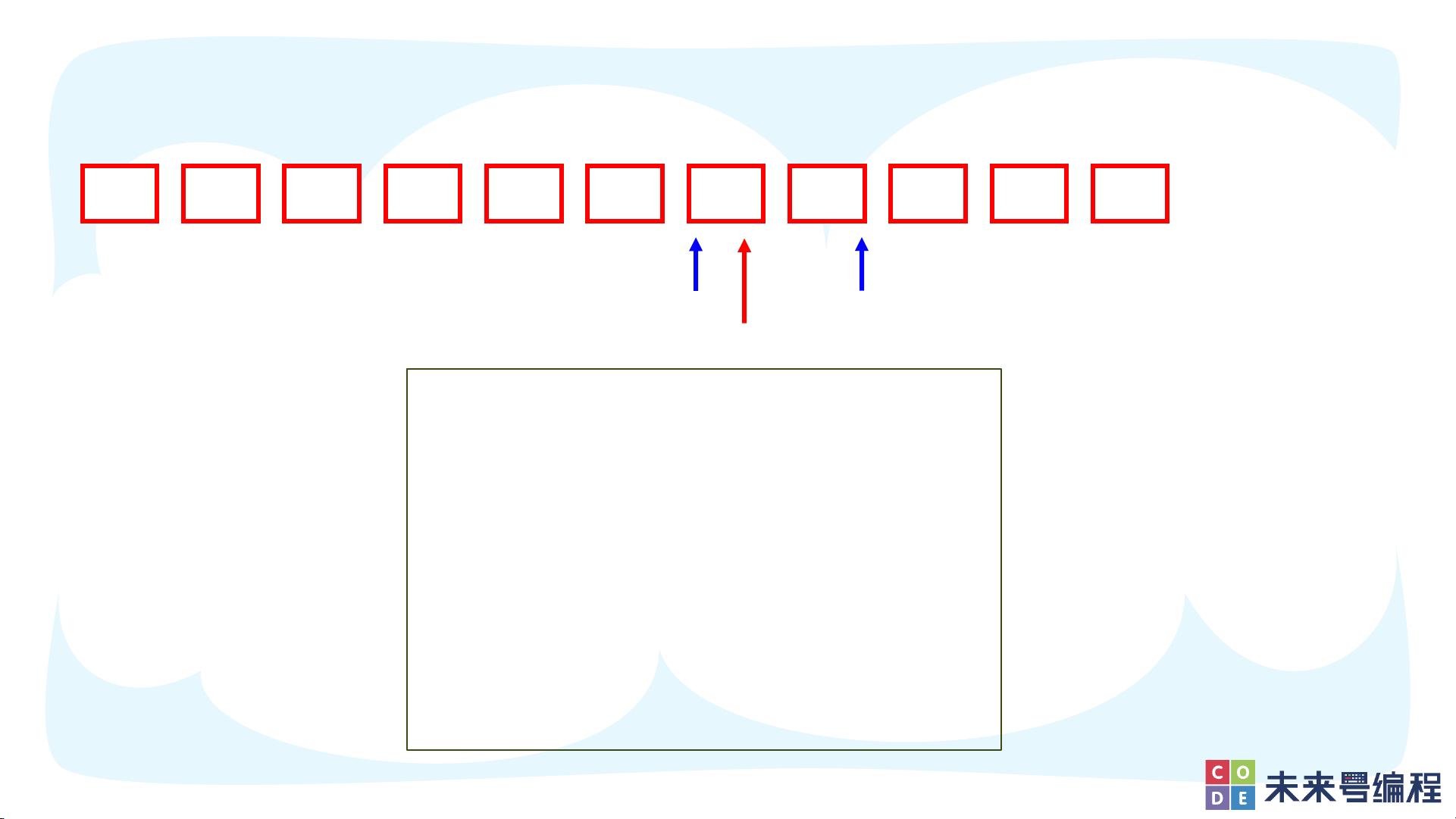
除了基本的查找目标值,二分算法还可以用于寻找特定条件的元素。例如,对于一个从小到大排序的数组,可以使用二分查找找到小于等于目标值x且最接近x的数。在这种情况下,我们可以在比较时根据目标值与中间元素的关系,选择向左还是向右查找。
此外,文件中还提到了一个具体的例子:给定一个单调递增的正整数序列,找出序列中最后一个小于等于k的数。这同样可以通过二分查找解决。输入包含序列长度n和目标值k,以及序列本身。对于给定的样例输入:
```
11 50
1 2 21 30 35 38 40 48 55 56 60 64
```
样例输出应为48,因为48是序列中最后一个不大于50的数。
二分查找算法在实际问题中有着广泛的应用,如在大规模数据中快速定位、查找最近点、求解最值问题等。理解并掌握二分算法及其变种,对于提升编程能力,特别是处理数据搜索和优化问题的能力,具有重要意义。
114 浏览量
214 浏览量
141 浏览量
2023-02-27 上传
113 浏览量
256 浏览量
2021-10-06 上传
186 浏览量
cdming
- 粉丝: 89
最新资源
- A7Demo.appstudio:探索JavaScript应用开发
- 百度地图范围内的标注点技术实现
- Foobar2000绿色汉化版:全面提升音频播放体验
- Rhythm Core .NET库:字符串与集合扩展方法详解
- 深入了解Tomcat源码及其依赖包结构
- 物流节约里程法的文档整理与实践分享
- NUnit3.vsix:快速安装NUnit三件套到VS2017及以上版本
- JQuery核心函数使用速查手册详解
- 多种风格的Select下拉框美化插件及其js代码下载
- Mac用户必备:SmartSVN版本控制工具介绍
- ELTE IK Web编程与Web开发课程内容详解
- QuartusII环境下的Verilog锁相环实现
- 横版过关游戏完整VC源码及资源包
- MVC后台管理框架2021版:源码与代码生成器详解
- 宗成庆主讲的自然语言理解课程PPT解析
- Memcached与Tomcat会话共享与Kryo序列化配置指南