Published as a conference paper at ICLR 2020
V × E. This can easily result in a model with billions of parameters, most of which are only updated
sparsely during training.
Therefore, for ALBERT we use a factorization of the embedding parameters, decomposing them
into two smaller matrices. Instead of projecting the one-hot vectors directly into the hidden space of
size H, we first project them into a lower dimensional embedding space of size E, and then project
it to the hidden space. By using this decomposition, we reduce the embedding parameters from
O(V × H) to O(V × E + E × H). This parameter reduction is significant when H E. We
choose to use the same E for all word pieces because they are much more evenly distributed across
documents compared to whole-word embedding, where having different embedding size (Grave
et al. (2017); Baevski & Auli (2018); Dai et al. (2019) ) for different words is important.
Cross-layer parameter sharing. For ALBERT, we propose cross-layer parameter sharing as an-
other way to improve parameter efficiency. There are multiple ways to share parameters, e.g., only
sharing feed-forward network (FFN) parameters across layers, or only sharing attention parameters.
The default decision for ALBERT is to share all parameters across layers. All our experiments
use this default decision unless otherwise specified. We compare this design decision against other
strategies in our experiments in Sec. 4.5.
Similar strategies have been explored by Dehghani et al. (2018) (Universal Transformer, UT) and
Bai et al. (2019) (Deep Equilibrium Models, DQE) for Transformer networks. Different from our
observations, Dehghani et al. (2018) show that UT outperforms a vanilla Transformer. Bai et al.
(2019) show that their DQEs reach an equilibrium point for which the input and output embedding
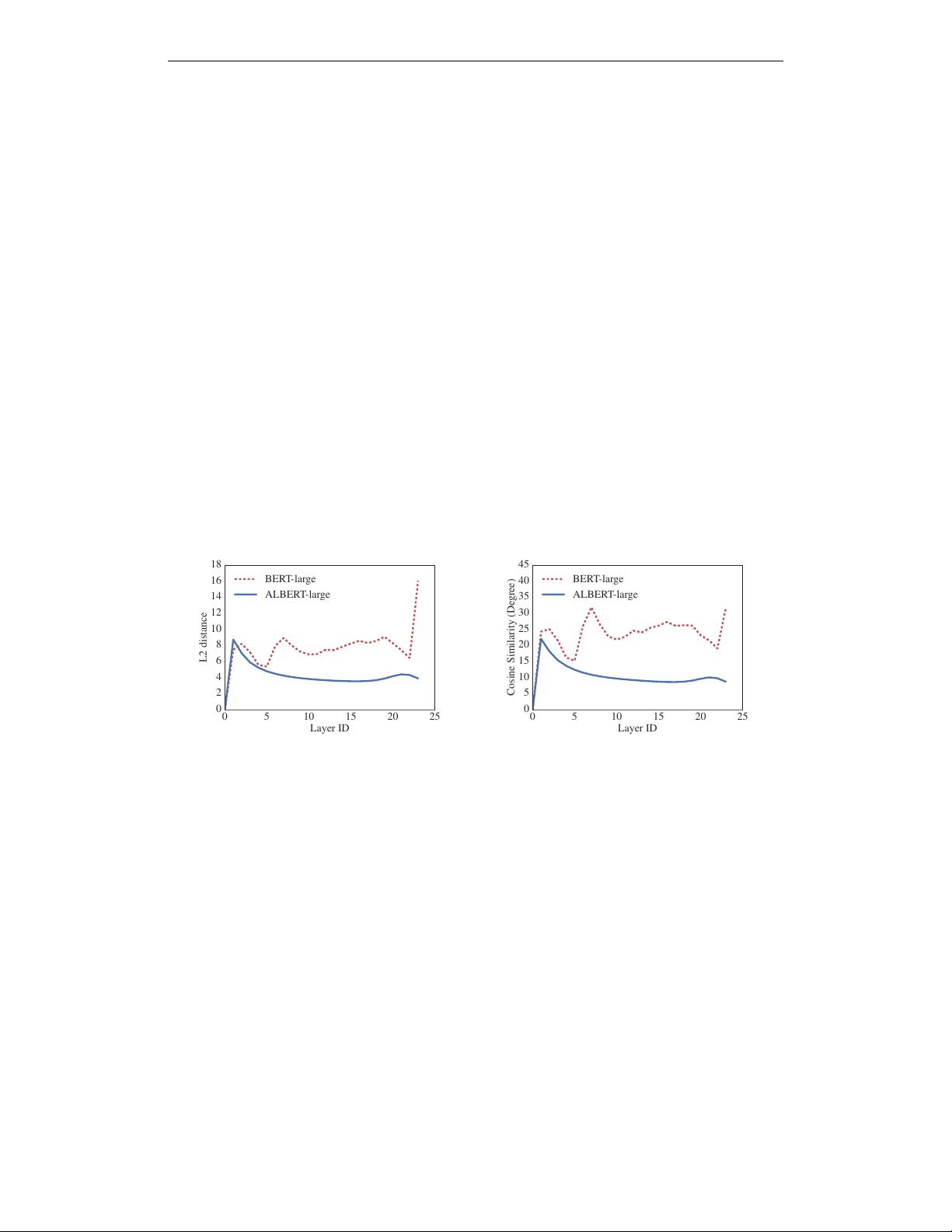
of a certain layer stay the same. Our measurement on the L2 distances and cosine similarity show
that our embeddings are oscillating rather than converging.
0 5 10 15 20 25
Layer ID
0
2
4
6
8
10
12
14
16
18
L2 distance
BERT-large
ALBERT-large
0 5 10 15 20 25
Layer ID
0
5
10
15
20
25
30
35
40
45
Cosine Similarity (Degree)
BERT-large
ALBERT-large
Figure 1: The L2 distances and cosine similarity (in terms of degree) of the input and output embed-
ding of each layer for BERT-large and ALBERT-large.
Figure 1 shows the L2 distances and cosine similarity of the input and output embeddings for each
layer, using BERT-large and ALBERT-large configurations (see Table 1). We observe that the tran-
sitions from layer to layer are much smoother for ALBERT than for BERT. These results show that
weight-sharing has an effect on stabilizing network parameters. Although there is a drop for both
metrics compared to BERT, they nevertheless do not converge to 0 even after 24 layers. This shows
that the solution space for ALBERT parameters is very different from the one found by DQE.
Inter-sentence coherence loss. In addition to the masked language modeling (MLM) loss (De-
vlin et al., 2019), BERT uses an additional loss called next-sentence prediction (NSP). NSP is a
binary classification loss for predicting whether two segments appear consecutively in the original
text, as follows: positive examples are created by taking consecutive segments from the training
corpus; negative examples are created by pairing segments from different documents; positive and
negative examples are sampled with equal probability. The NSP objective was designed to improve
performance on downstream tasks, such as natural language inference, that require reasoning about
the relationship between sentence pairs. However, subsequent studies (Yang et al., 2019; Liu et al.,
2019) found NSP’s impact unreliable and decided to eliminate it, a decision supported by an im-
provement in downstream task performance across several tasks.
We conjecture that the main reason behind NSP’s ineffectiveness is its lack of difficulty as a task,
as compared to MLM. As formulated, NSP conflates topic prediction and coherence prediction in a
4









