超启发式算法的低级参数自适应与启发式空间缩减：实证评估

119 浏览量更新于2024-07-14 1 收藏 1.95MB PDF 举报

本文主要探讨了在超启发式算法中引入低级参数自适应（Low-Level Parameters Adaptation, LLP）功能的重要性，尤其是在面对具有参数化低级启发式算法（Low-Level Heuristics, LLHs）的问题时。超启发式算法是一种高级搜索策略，通过组合和控制一组基础算法来解决复杂问题，其目标是提高算法设计的灵活性和泛化能力，减少对特定问题领域的依赖。传统超启发式方法中，LLHs通常预设固定的参数，这与超启发式寻求领域无关性的理念相悖。作者提出了一个名为AD-HH（具有LLP自适应功能的超启发式）的新方法，该方法的核心在于能够自动调整LLPs，以适应不同的问题实例。通过自适应地维护两个超启发式模型的LLPs，AD-HH增强了搜索策略的动态性，使得算法能够更好地应对各种问题特征。文章强调了LLP适应可能导致的搜索空间扩大问题，因此作者引入了启发式空间缩减（Space Reductions, SAR）机制，作为一种有效的解决方案。SAR机制帮助AD-HH框架更高效地探索和管理可能的参数组合，同时避免了因参数调整带来的过大规模搜索。作者选取p中值问题作为实验的基准案例，实验结果显示，AD-HH通过整合LLP自适应和SAR机制，在三个不同类型的基准实例上展现了强大的性能，其结果具有竞争力，证明了这种新型超启发式方法的有效性和实用性。本文的主要贡献在于提出了一种创新的超启发式策略，即AD-HH，它通过自动调整低级参数和应用启发式空间缩减机制，实现了超启发式算法在实际问题上的更高效和灵活应用，有望在未来为优化问题求解提供新的解决方案。

Hyper-Heuristics with Low Level Parameter Adaptation

Adaptive. In this approach, the values of the parameters are maintained based

on the feedback information collected from the search procedure, which may

involve the quality of the solution, the diversity of the population, and so on.

Thus, this approach can also be considered similar to perturbative LLH selection-

based hyper-heuristics, as well as DMAB-based operator selection (DaCosta et al.,

2008), since all these approaches are based on the communication of the feedback

information. For example, the classical 1/5 rule in evolution strategy (ES) is an

adaptive parameter control approach (Rechenberg, 1973). Y. Li and W. Li (2007)

developed an adaptive ant-based algorithm, in which the parameters α and β are

adaptively adjusted based on entropy calculation.

Self-Adaptive. Instead of interacting with the search procedure according to

some feedback information, in self-adaptive approaches, the parameters are en-

coded into the solution, and get optimized along with the exploration of the so-

lution space. One example is the σ -self-adaptation in ES investigated by Hansen

(2006). Serpell and Smith (2010) discussed the self-adaptation of the mutation op-

erator for the permutation representations. See Meyer-Nieberg and Beyer (2007)

for a survey of self-adaptive parameter control.

This concludes the introduction of both hyper-heuristics and parameter setting

techniques. Interestingly, we observe that these two research directions have much in

common. From the perspective of motivations, both directions aim at preventing the

algorithms from being instance and/or problem dependent. From the perspective of

methodologies, these two directions can also be considered relevant, especially when

we compare perturbative LLH selection-based hyper-heuristics and adaptive param-

eter control approaches. Thus, in this paper, we intend to integrate perturbative LLH

selection-based hyper-heuristics and adaptive parameter control into a uniﬁed frame-

work, so as to improve the generality and the robustness of hyper-heuristics.

3 Hyper-Heuristics with Low Level Parameter Adaptation

As mentioned in Section 1, static LLP conﬁgurations may suffer from a series of prob-

lems, such as the training overhead, as well as the generality issue. As a solution, we

intend to propose a general framework that incorporates the LLP adaptation.

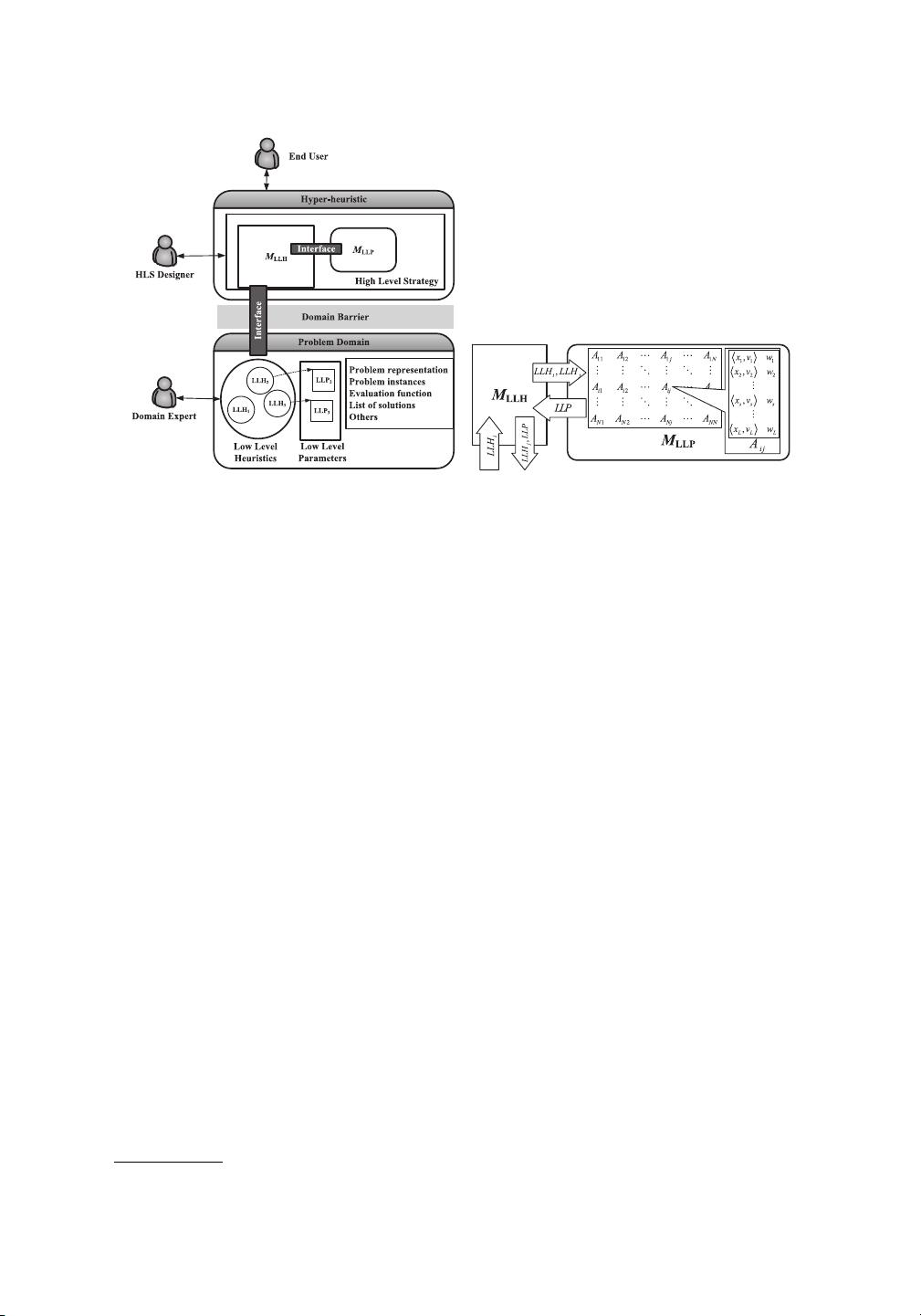
The main idea of AD-HH is simple. In the framework, the HLS is further decom-

posed into two modules, the LLH management module (denoted as M

LLH

), and the

LLP management module (denoted as M

LLP

). On one hand, M

LLH

selects, applies, and

evaluates the LLHs in a similar way as most of the existing hyper-heuristics. On the

other hand, M

LLP

is responsible for the selection and evaluation of LLPs. Figure 2(a)

describes the framework diagram, in which the two modules communicate with each

other so as to pass the values of LLPs, the feedback information about the quality of

the applied LLPs, and so on. Note that since the maintenance of the LLPs is achieved

through the information exchange between M

LLH

and M

LLP

, the LLP adaptation in this

study should be classiﬁed as an adaptive parameter control approach (see Section 2).

More speciﬁcally, our framework consists of the following components: H, Q,

S, M

LLH

,andM

LLP

. Among these components, H ={LLH

, LLH

,...,LLH

} in-

dicates the set of LLHs, where N is the number of the LLHs, Q ={q

,...,q

num

} is

a population of num LLH sequences. In the population, each sequence is deﬁned as

=q

,...,q

len

, where q

∈ H is the jth LLH of the ith sequence in Q,andlen

Evolutionary Computation Volume 20, Number 2 195

Z. Ren, H. Jiang, J. Xuan, and Z. Luo

(a) (b)

Figure 2: Hyper-heuristic with LLP adaptation. (a) AD-HH framework. (b) Illustration

of the LLP generation.

indicates the length of each LLH sequence. Associated with each LLH sequence q

, there

exists a feasible solution s

, over which the LLHs of q

are applied, and the population

of the solutions is deﬁned as S ={s

,...,s

num

Finally, M

LLH

and M

LLP

are the

modules to manipulate the population of LLH sequences and LLPs, respectively.

With each component of the framework speciﬁed, we now present the pseudocode

of AD-HH in Algorithm 1. Before the main loop, several components are initialized,

including the initial LLH sequence population Q



, the initial solution population S



LLH

,andM

LLP

(lines 2–4). Then, at each generation of the main loop, a new LLH

sequence population Q is ﬁrst constructed with respect to the population Q



of the

previous generation, and/or some other auxiliary information (line 6). After that, each

LLH sequence q

∈ Q is applied over s

for actual problem solving. Unlike most of the

existing hyper-heuristics, in this study, the LLHs may be parameterized. As a solution,

before invoking the parameterized LLH, the corresponding LLP is to be selected us-

ing M

LLP

(lines 10–11). When a sequence of LLHs is executed (line 12), and returns the

feedback information, the information is used to evaluate the LLHs and the correspond-

ing LLPs (line 13). Once all the LLH sequences in the population have been applied,

the LLH sequence population Q



for the next generation is to be selected (line 14). In

this study, binary tournament selection is employed. Meanwhile, the selection of S



implicitly conducted, since each LLH sequence corresponds to a feasible solution. Fi-

nally, if necessary, the structures of M

LLH

and M

LLP

are updated (line 16).

Note that AD-HH is a generic framework in which several interfaces (underlined

in Algorithm 1) have to be implemented so that the framework can be instantiated

for problem solving. For example, we have to provide an M

LLH

speciﬁc method to

construct new LLH sequences (line 6), an M

LLP

speciﬁc method to assign LLP values

By associating each LLH sequence with a solution, the quality of the LLH sequences can easily be

measured using the objective values of their corresponding solutions.

196 Evolutionary Computation Volume 20, Number 2

剩余38页未读，继续阅读

weixin_38691739

粉丝: 6
资源: 958

超启发式算法的低级参数自适应与启发式空间缩减：实证评估

packing_java_超启发式算法_

Flow shop超启发算法.zip

具有低级参数自适应的超启发式

Hyper-heuristic_Hyper-heuristic_hyperheuristic_multi-objective_超

多智能体超启发式算法在多目标航空发动机叶片制造中的应用

MiniGui业务开发基础培训-htk

com.harmonyos.exception.DiskReadWriteException(解决方案).md

网络分析-Wireshark数据包筛选技巧详解及应用实例

com.harmonyos.exception.BatteryOverheatException(解决方案).md

com.harmonyos.exception.ServiceUnavailableException(解决方案).md

最新资源